比较全面的L1和L2正则化的解释
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
本文转自|机器学习算法那些事
前言
前段时间写了一篇文章《深入理解线性回归算法(二):正则项的详细分析》,文章提到L1是通过稀疏参数(减少参数的数量)来降低复杂度,L2是通过减小参数值的大小来降低复杂度。网上关于L1和L2正则化降低复杂度的解释五花八门,易让人混淆,看完各种版本的解释后过几天又全部忘记了。因此,文章的内容总结了网上各种版本的解释,并加上了自己的理解,希望对大家有所帮助。
目录
1、优化角度分析
2、梯度角度分析
3、先验概率角度分析
4、知乎点赞最多的图形角度分析
5、限制条件角度分析
6.、PRML的图形角度分析
7、总结

1、L2正则化的优化角度分析

在限定的区域,找到使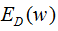 最小的值。
最小的值。
图形表示为:
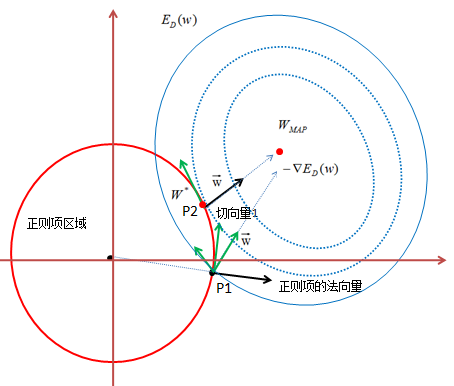
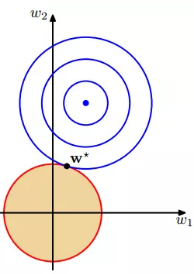
上图所示,红色实线是正则项区域的边界,蓝色实线是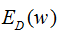 的等高线,越靠里的等高圆,
的等高线,越靠里的等高圆,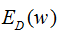 越小,梯度的反方向是
越小,梯度的反方向是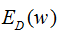 减小最大的方向,用
减小最大的方向,用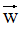 表示,正则项边界的法向量用实黑色箭头表示。
表示,正则项边界的法向量用实黑色箭头表示。
正则项边界在点P1的切向量有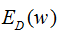 负梯度方向的分量,所以该点会有往相邻的等高虚线圆运动的趋势;当P1点移动到P2点,正则项边界在点P2的切向量与
负梯度方向的分量,所以该点会有往相邻的等高虚线圆运动的趋势;当P1点移动到P2点,正则项边界在点P2的切向量与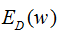 梯度方向的向量垂直,即该点没有往负梯度方向运动的趋势;所以P2点是
梯度方向的向量垂直,即该点没有往负梯度方向运动的趋势;所以P2点是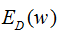 最小的点。
最小的点。
结论:L2正则化项使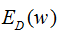 值最小时对应的参数变小。
值最小时对应的参数变小。
2、L1正则化的优化角度分析

在限定的区域,找到使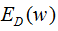 最小的值。
最小的值。
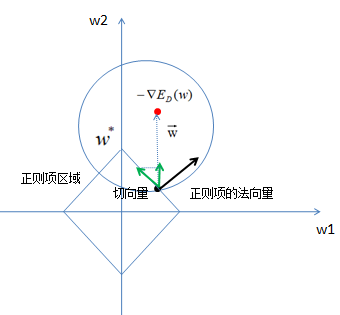
结论:如上图,因为切向量始终指向w2轴,所以L1正则化容易使参数为0,即特征稀疏化。
1、L1正则化
L1正则化的损失函数为:
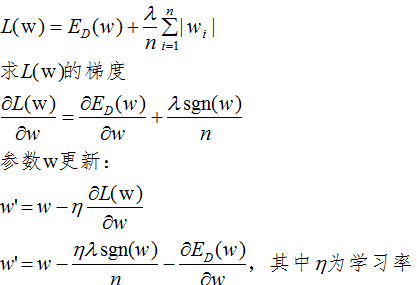
上式可知,当w大于0时,更新的参数w变小;当w小于0时,更新的参数w变大;所以,L1正则化容易使参数变为0,即特征稀疏化。
2、L2正则化
L2正则化的损失函数为:
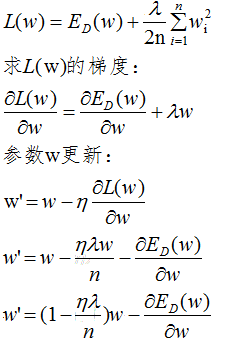
由上式可知,正则化的更新参数相比于未含正则项的更新参数多了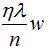 项,当w趋向于0时,参数减小的非常缓慢,因此L2正则化使参数减小到很小的范围,但不为0。
项,当w趋向于0时,参数减小的非常缓慢,因此L2正则化使参数减小到很小的范围,但不为0。
文章《深入理解线性回归算法(二):正则项的详细分析》提到,当先验分布是拉普拉斯分布时,正则化项为L1范数;当先验分布是高斯分布时,正则化项为L2范数。本节通过先验分布来推断L1正则化和L2正则化的性质。
画高斯分布和拉普拉斯分布图(来自知乎某网友):
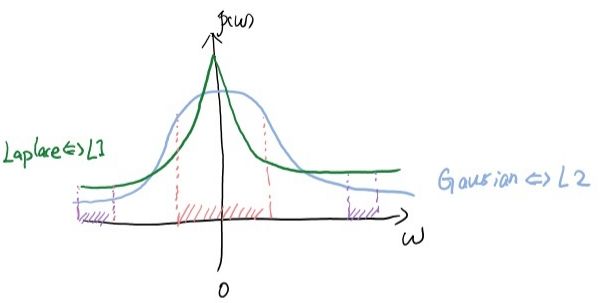
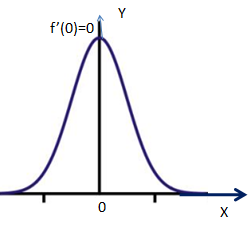
由上图可知,拉普拉斯分布在参数w=0点的概率最高,因此L1正则化相比于L2正则化更容易使参数为0;高斯分布在零附近的概率较大,因此L2正则化相比于L1正则化更容易使参数分布在一个很小的范围内。
函数极值的判断定理:
(1)当该点导数存在,且该导数等于零时,则该点为极值点;
(2)当该点导数不存在,左导数和右导数的符号相异时,则该点为极值点。
如下面两图:
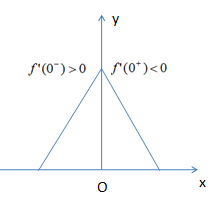
左图对应第一种情况的极值,右图对应第二种情况的极值。本节的思想就是用了第二种极值的思想,只要证明参数w在0附近的左导数和右导数符合相异,等价于参数w在0取得了极值。
图形角度分析
损失函数L如下:
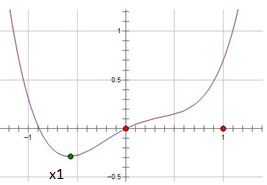
黑色点为极值点x1,由极值定义:L'(x1)=0;
含L2正则化的损失函数: 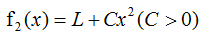

由结论可定性的画含L2正则化的图:
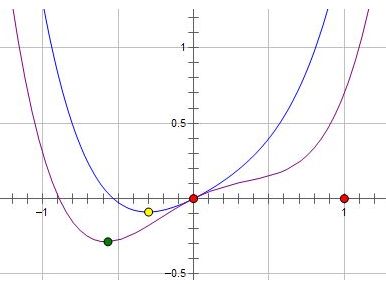
极值点为黄色点,即正则化L2模型的参数变小了。
含L1正则化的损失函数: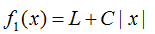

因此,只要C满足推论的条件,则损失函数在0点取极值(粉红色曲线),即L1正则化模型参数个数减少了。
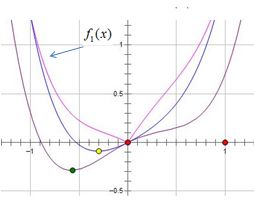
这种思想还是来自知乎的,觉得很有趣,所以就记录在这篇文章了,思想用到了凸函数的性质。我就直接粘贴这种推导了,若有不懂的地方请微信我。

结论:含L1正则化的损失函数在0点取得极值的条件比相应的L2正则化要宽松的多,所以,L1正则化更容易得到稀疏解(w=0)。
因为L1正则化在零点附近具有很明显的棱角,L2正则化则在零附近比较平缓。所以L1正则化更容易使参数为零,L2正则化则减小参数值,如下图。
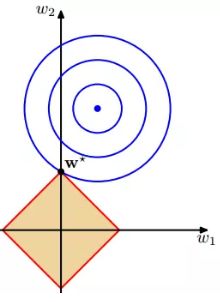
(1)L1正则化使参数为零 (2)L2正则化使参数减小
本文总结了自己在网上看到的各种角度分析L1正则化和L2正则化降低复杂度的问题,希望这篇文章能够给大家平时在检索相关问题时带来一点帮助。若有更好的想法,期待您的精彩回复,文章若有不足之处,欢迎更正指出。
参考:
https://www.zhihu.com/question/37096933
林轩田老师 《机器学习基石》
好消息,小白学视觉团队的知识星球开通啦,为了感谢大家的支持与厚爱,团队决定将价值149元的知识星球现时免费加入。各位小伙伴们要抓住机会哦!

交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

