图解 | LeetCode #235 二叉搜索树的最近公共祖先
👇👇关注后回复 “进群” ,拉你进程序员交流群👇👇
作者丨微木
来源丨编程狂想曲
你好,我是微木。
今天分享的内容是LeetCode中235.二叉搜索树的最近公共祖先 简单 这个题目。
题目描述:
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
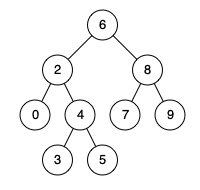
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
思路分析
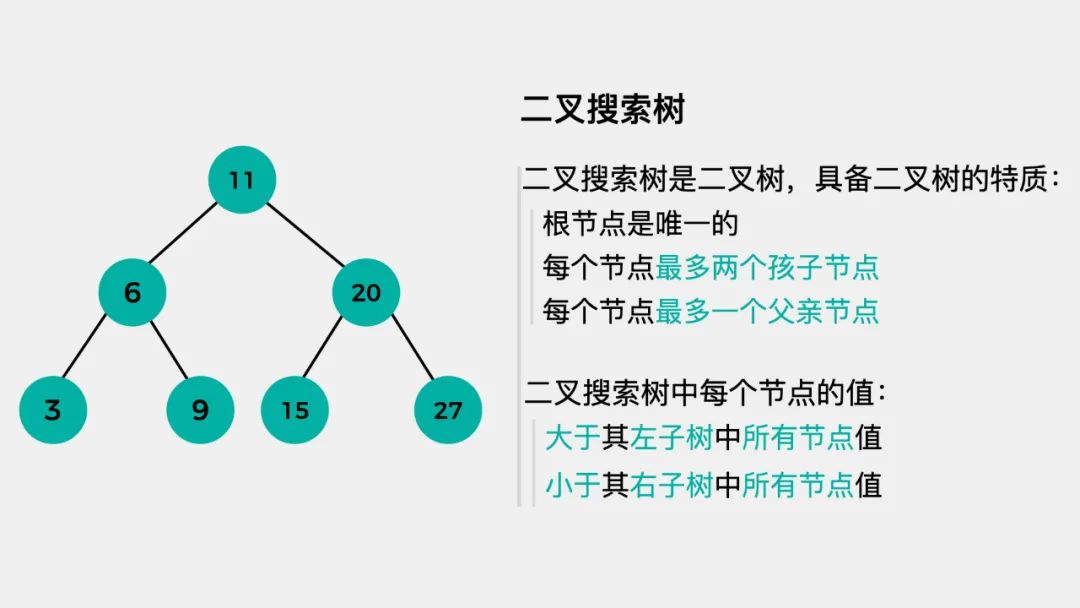
二叉搜索树的主要性质如下图:
根据题目描述,可以确定两个节点p和q,一定在二叉搜索树中。那么,相比较于根节点root而言,这两个节点有如下几种情况:
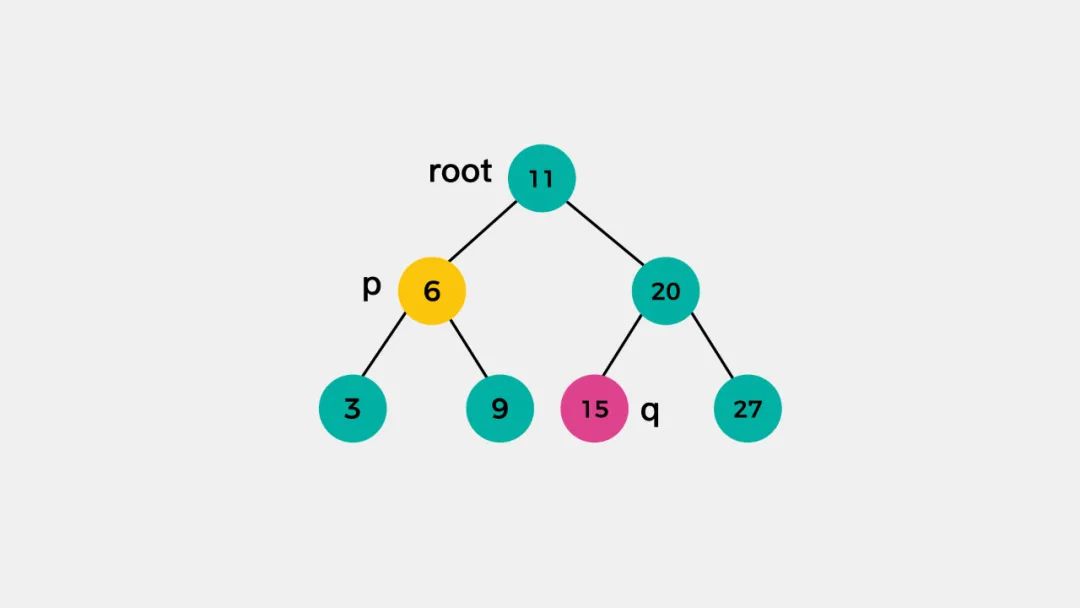
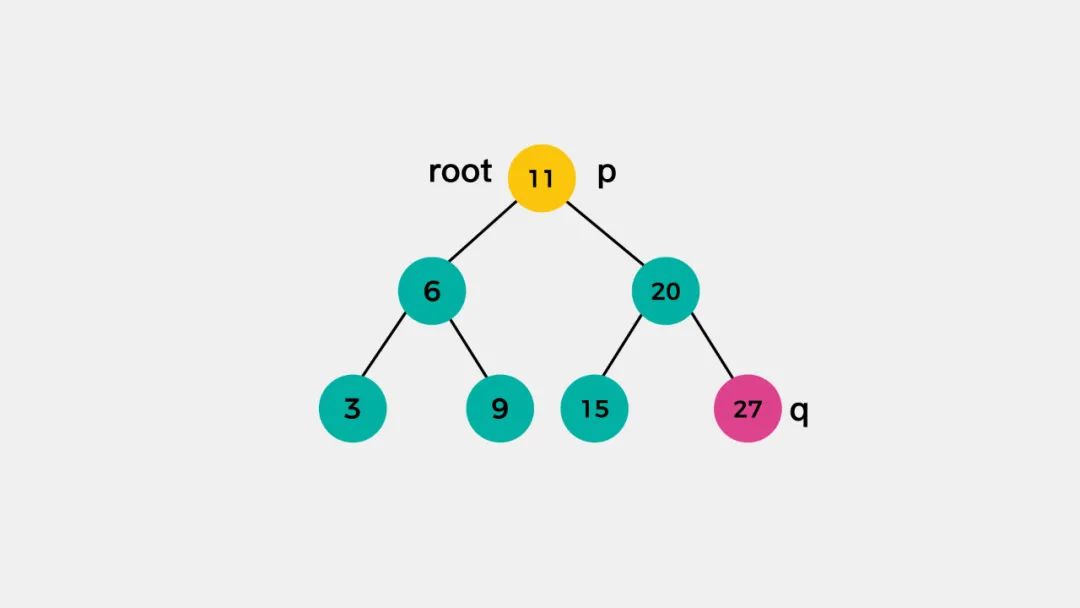
1.p和q,一个在root的左子树,一个在root的右子树
对于这种情况,p和q的最近公共祖先就是根节点root。
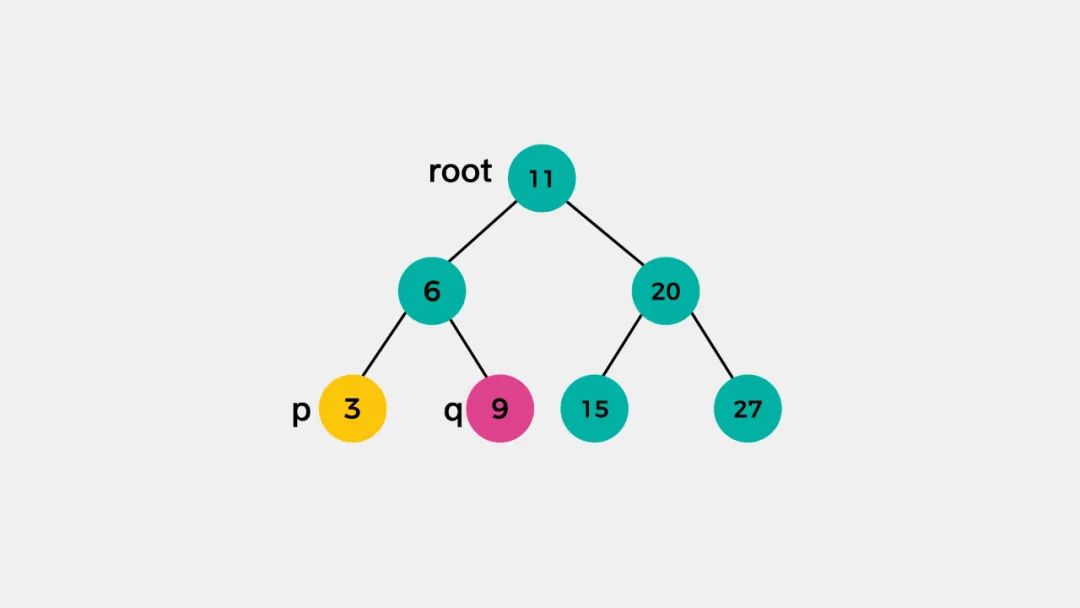
2.p和q,都在root的左子树
对于这种情况,p和q的公共祖先,需要在左子树查找。就节点p=3和节点q=9来说,它们的最近公共祖先是节点6。
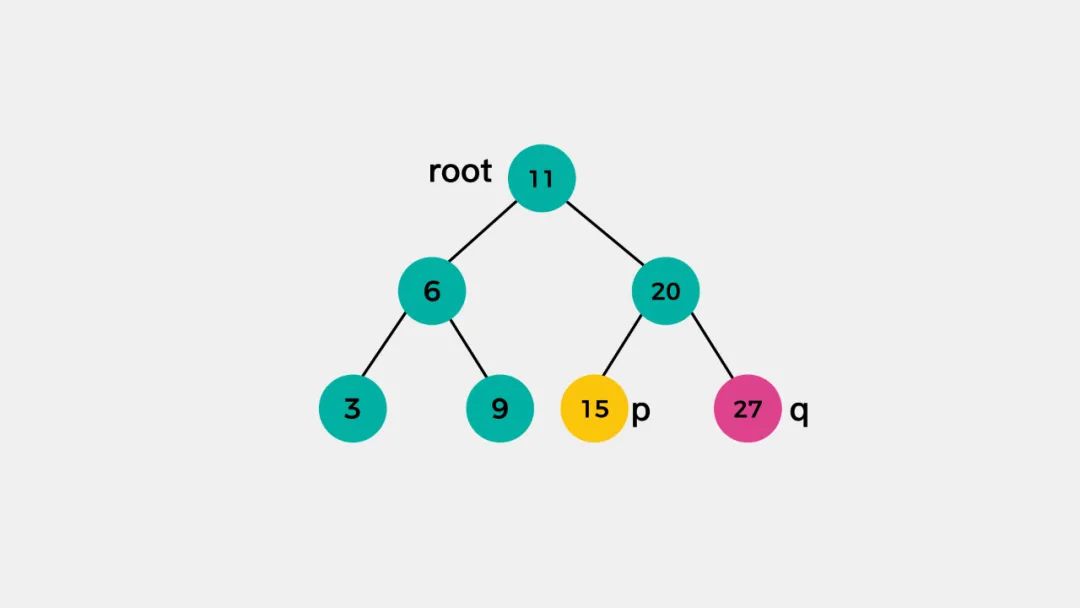
3.p和q,都在root的右子树
对于这种情况,p和q的公共祖先需要在根节点root的右子树查找。就节点15和27而言,它们的最近公共祖先是节点20。
4.p和q,其中一个节点就是根节点
对于这种情况,根据公共祖先的定义,与根节点相同的节点就是它们的最近公共祖先。这里,节点p和节点q的最近公共祖先是根节点root,也是节点p。
根据上述四种情况的分析,总结来说就是:
当节点p和节点q都在左子树时,即都小于根节点root时,需要在root的左子树查找其最近公共祖先;
当节点p和节点q都在右子树时,即都大于根节点root时,需要在root的右子树查找其最近公共祖先;
当节点p和节点q一个在根节点root的左子树,一个在其右子树,或者其中一个节点和根节点相同时,root就是其最近公共祖先。
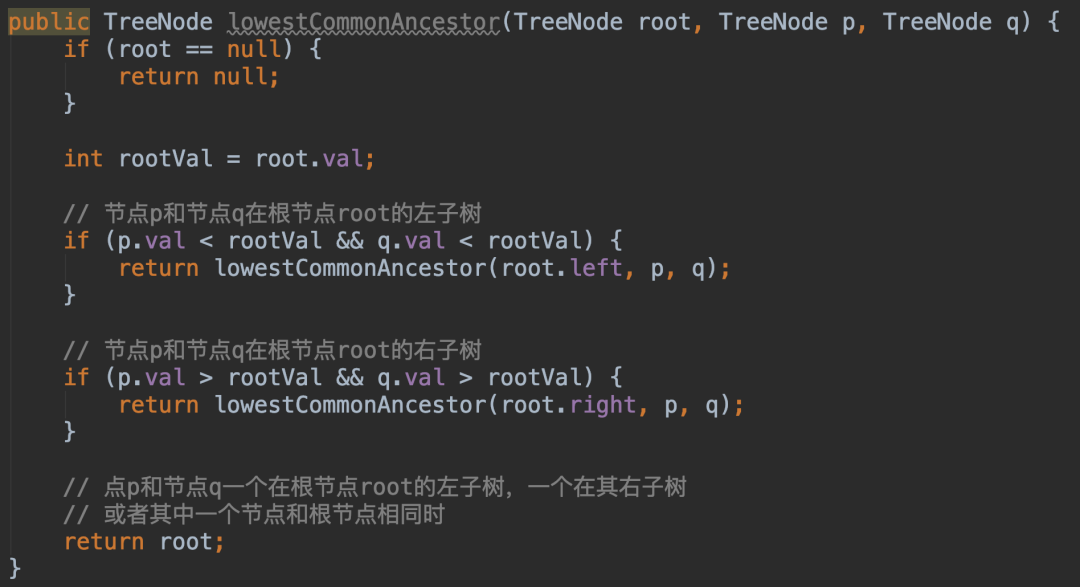
至此,根据二叉搜索树的天然递归属性,代码实现如下:
方法lowestCommonAncestor的用就是给定根节点root,然后找到节点p和q的最近公共祖先返回。因此,该方法就是递归函数。
那么,当需要在左子树或右子树中寻找节点p和节点q的最近公共祖先时,直接调用该方法就可以。
-End-
最近有一些小伙伴,让我帮忙找一些 面试题 资料,于是我翻遍了收藏的 5T 资料后,汇总整理出来,可以说是程序员面试必备!所有资料都整理到网盘了,欢迎下载!
点击👆卡片,关注后回复【
面试题】即可获取评论