[Formula&Excel&Python] 一次指数平滑、二次指数平滑、三次指数平滑...

- 一次指数平滑:适用于序列没有趋势和季节性特征
- 二次指数平滑:适用于序列有趋势特征但无季节性特征
- 三次指数平滑:适用于序列有趋势特征且有季节性特征
简单指数平滑
一次指数平滑中最常用的实现方法就是简单指数平滑,有时我们说指数平滑也是指的简单指数平滑(Single Exponential Smoothing)。参数:,平滑因子或平滑系数
预测方程:
平滑方程:
取值范围[0~1],值越大,越关注近期的观测值,远期的观测值影响越小。当时间序列相对平稳时,取较小的;当时间序列波动较大时,取较大的,以不忽略远期观测值的影响。
示例演示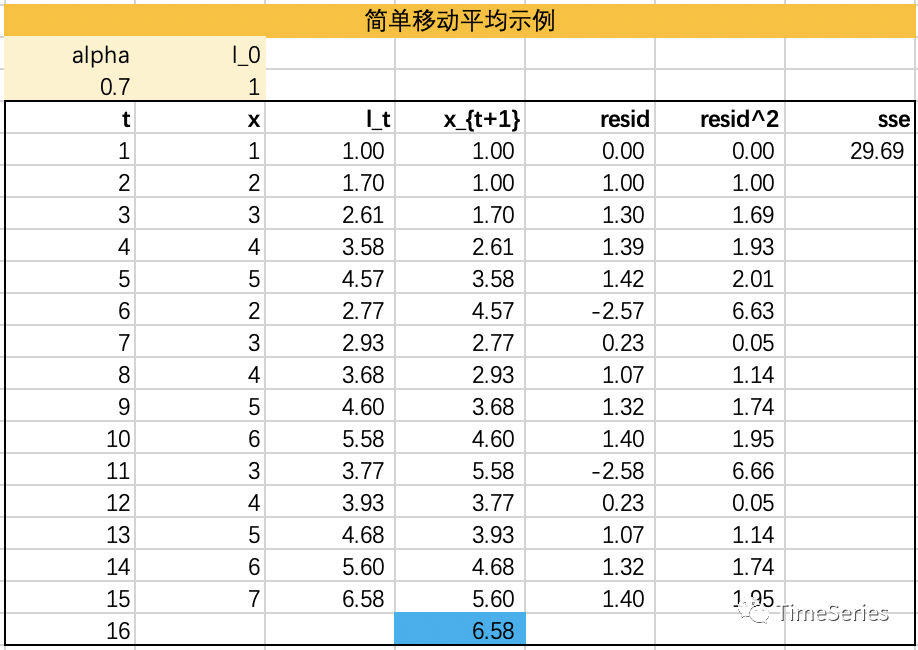
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
# 方法1,alpha=0.7
fit1 = SimpleExpSmoothing(data).fit(smoothing_level=0.7,optimized=False)
print('>> fit1', 'forecast:', fit1.forecast(3), 'sse:', fit1.sse)
# 方法2,不加任何参数,optimized默认为True,能自动选择alpha。
fit2 = SimpleExpSmoothing(data).fit()
print('>> fit2', 'forecast:', fit2.forecast(3), 'sse:', fit2.sse)

二次指数平滑推荐使用方法2,自动识别最优参数。statsmodels中通过最小化平滑值和实际值的欧式距离确定最优参数,其实也可通过SSE、MAE、RMSE、SMAPE等评估指标确定最优参数。不使用自动优化时,和可根据场景经验确定,简单指数平滑中statsmodels中默认使用第一个观测值作为初始指数平滑的值。
二次指数平滑,也叫双指数平滑,是指数平滑的扩展。常用实现为Holt指数平滑,方法中包含一个预测方程和两个平滑方程(水平平滑方程+趋势预测方程)。
其中,趋势部分又可分为加性趋势和乘性趋势,分别对应Holt线性趋势模型、指数趋势模型。
对于较大时间步长的预测,趋势可能不会无限延长,就需要抑制这种趋势,加性趋势和乘性趋势的抑制分别对应加性抑制(抑制线性趋势)、乘性抑制(抑制指数趋势)。
Holt线性趋势模型
Holt 在1957年把简单的指数平滑模型进行了延伸,能够预测包含趋势的数据,参数1:,水平平滑因子,水平平滑参数
参数2:,趋势平滑因子,控制趋势变化的影响
预测方程:
水平方程:
趋势方程:
其中,代表时刻t的预估水平,代表时刻t的预测趋势,是水平的平滑参数,是趋势的平滑参数。
示例演示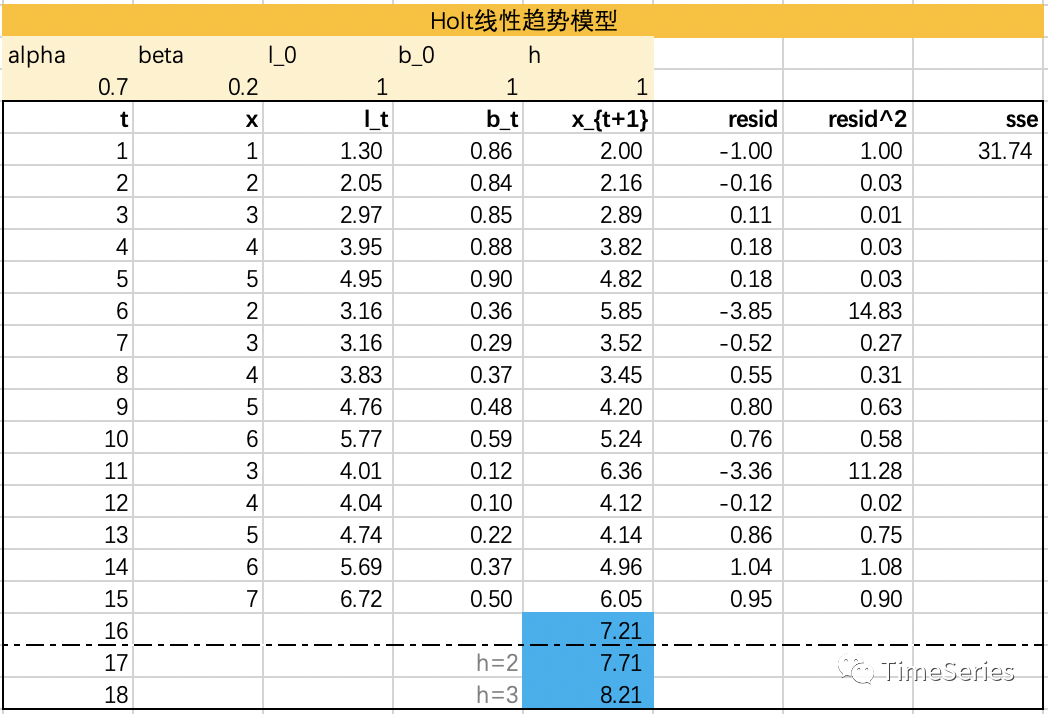
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
fit1 = Holt(data).fit(smoothing_level=0.7, smoothing_trend=0.2, optimized=False)
print(fit1.summary())
print('forecast:', fit1.forecast(3))
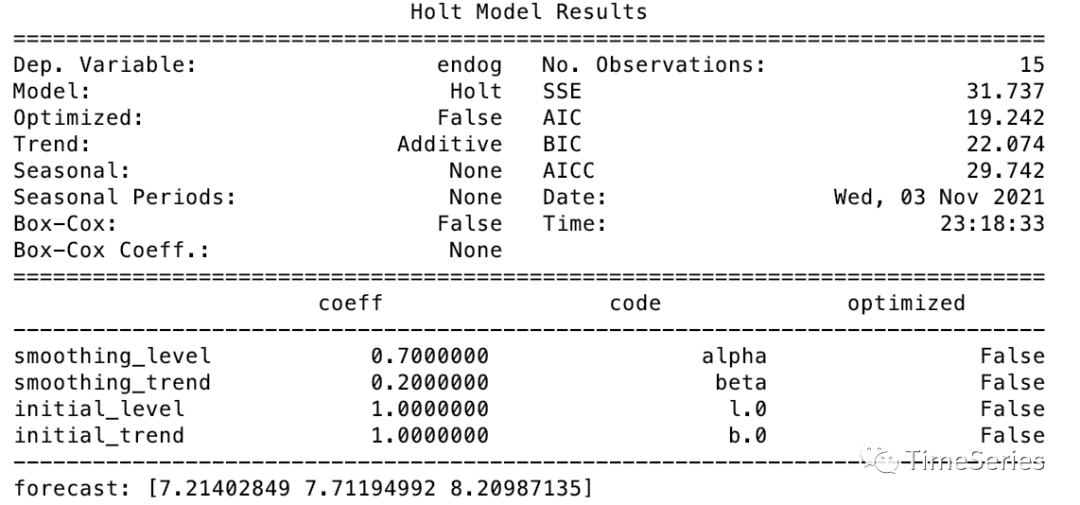
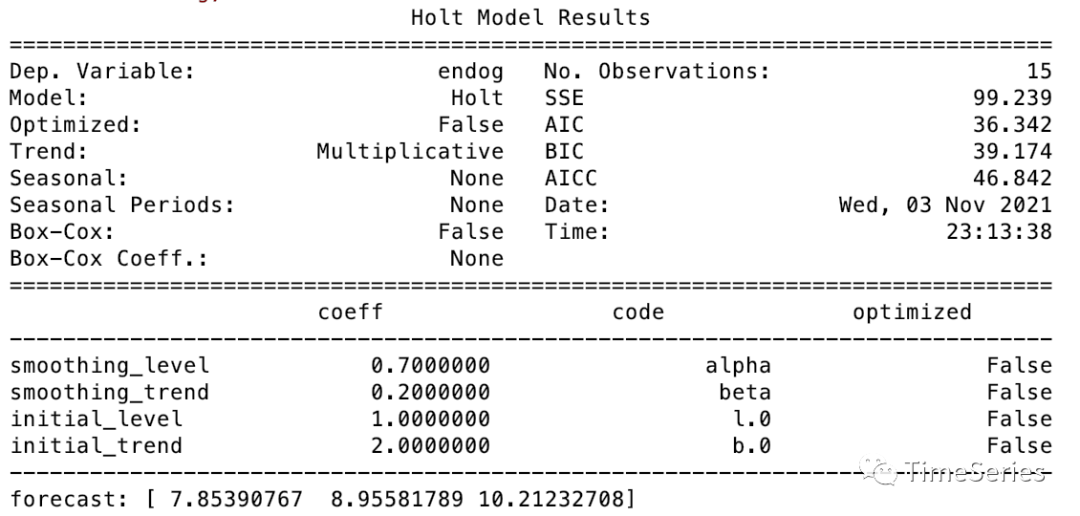
指数趋势模型
另外一种Holt 线性模型的变体是指数趋势模型,水平分量和趋势分量不再是相加的,而是相乘的。
参数1:,水平平滑因子
参数2:,趋势平滑因子
预测方程:
水平方程:
趋势方程:
其中,代表预估的增长率,描述指数趋势。
示例演示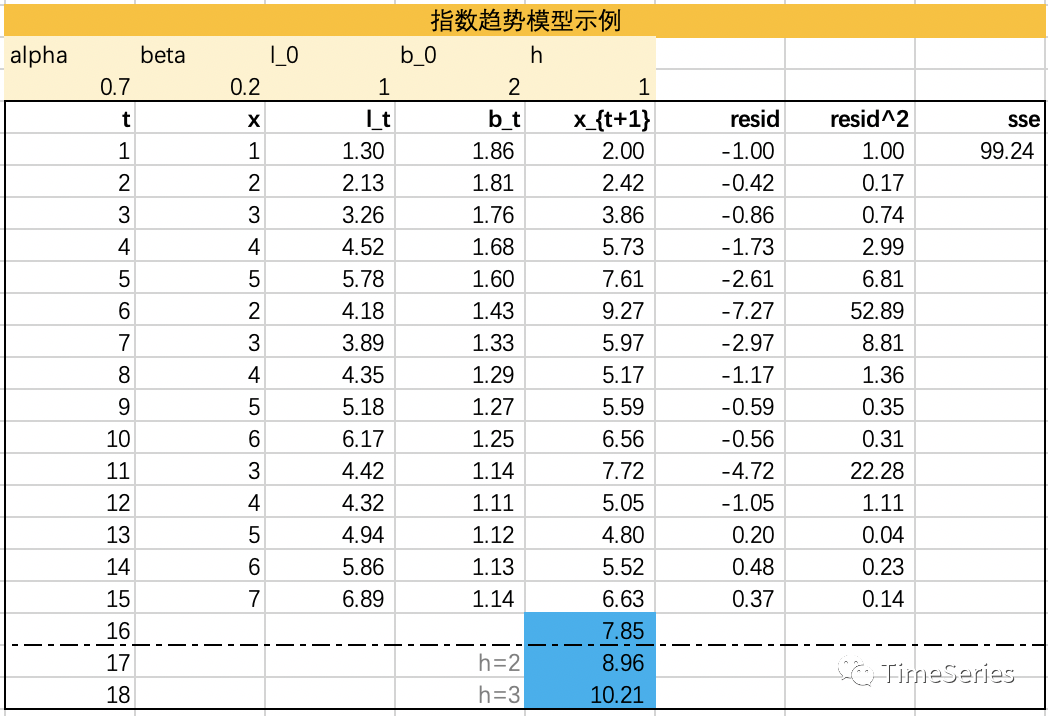
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
fit1 = Holt(data, exponential=True).fit(smoothing_level=0.7, smoothing_trend=0.2, optimized=False)
print(fit1.summary())
print('>> fit1', 'forecast:', fit1.forecast(3), 'sse:', fit1.sse)
阻尼趋势模型
Gardner 和 McKenzie (1985)引入了一种阻尼效应,未来的增长趋势会有所放缓。
参数1:,水平平滑因子
参数2:,趋势平滑因子
参数3:,0<<1,阻尼参数,防止预测“失控”
预测方程:
水平方程:
趋势方程:
其中,当时,等同于Holt线性趋势模型。
示例演示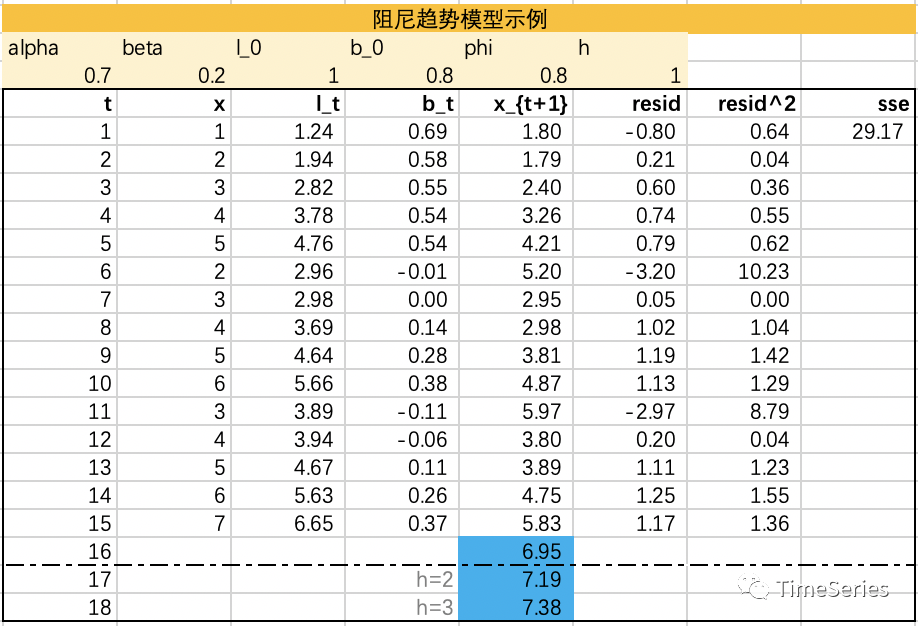
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
fit1 = Holt(data, exponential=False, damped_trend=True).fit(smoothing_level=0.7, smoothing_trend=0.2, damping_trend=0.8, optimized=False)
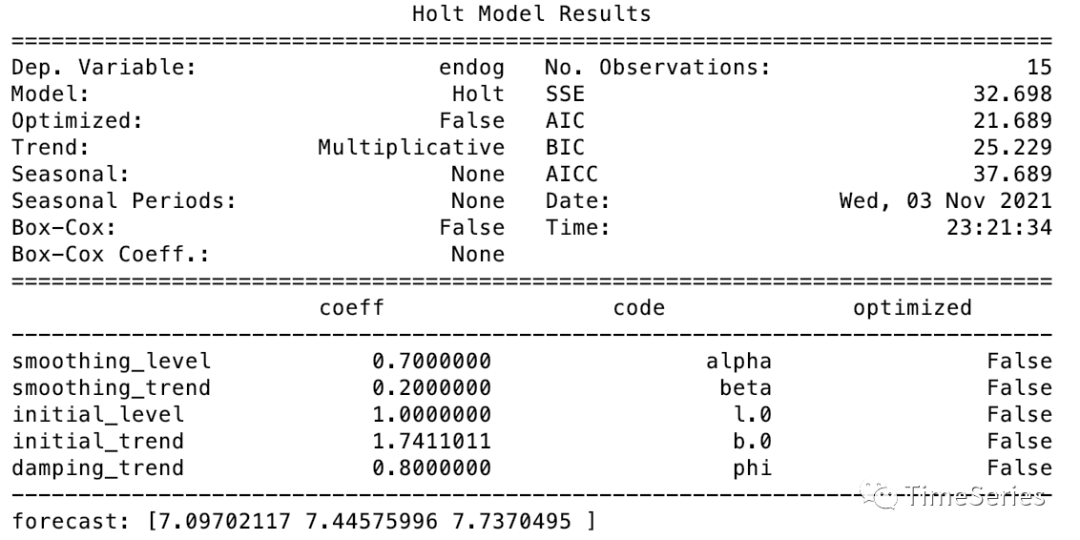
print(fit1.summary())
print('>> fit1', 'forecast:', fit1.forecast(3), 'sse:', fit1.sse)
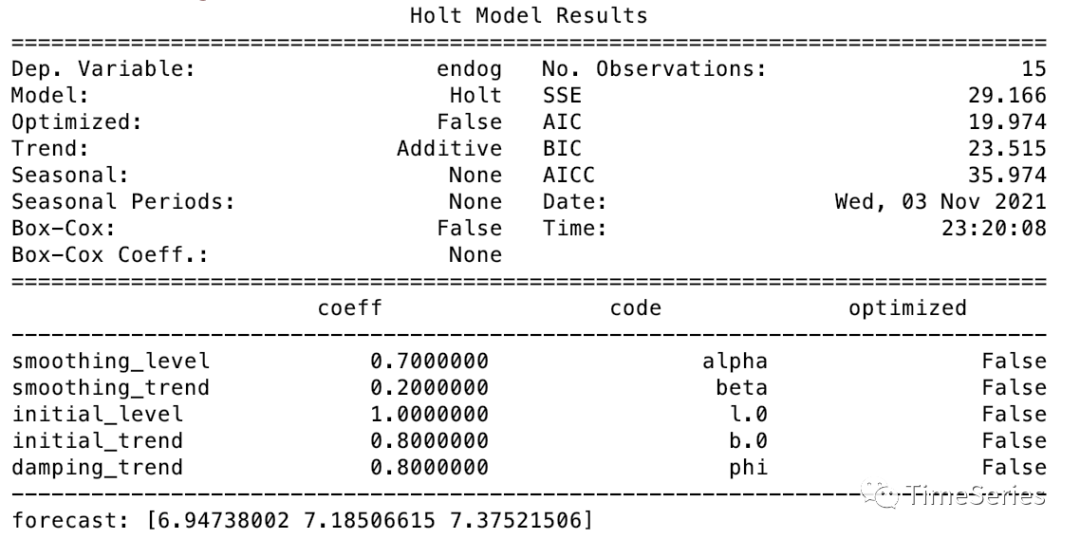
乘法阻尼趋势
Taylor(2003)将阻尼参数拓展到乘法模型,预测结果不像加法阻尼那么保守。
参数1:,水平平滑因子
参数2:,趋势平滑因子
参数3:,0<<1,阻尼参数
预测方程:
水平方程:
趋势方程:
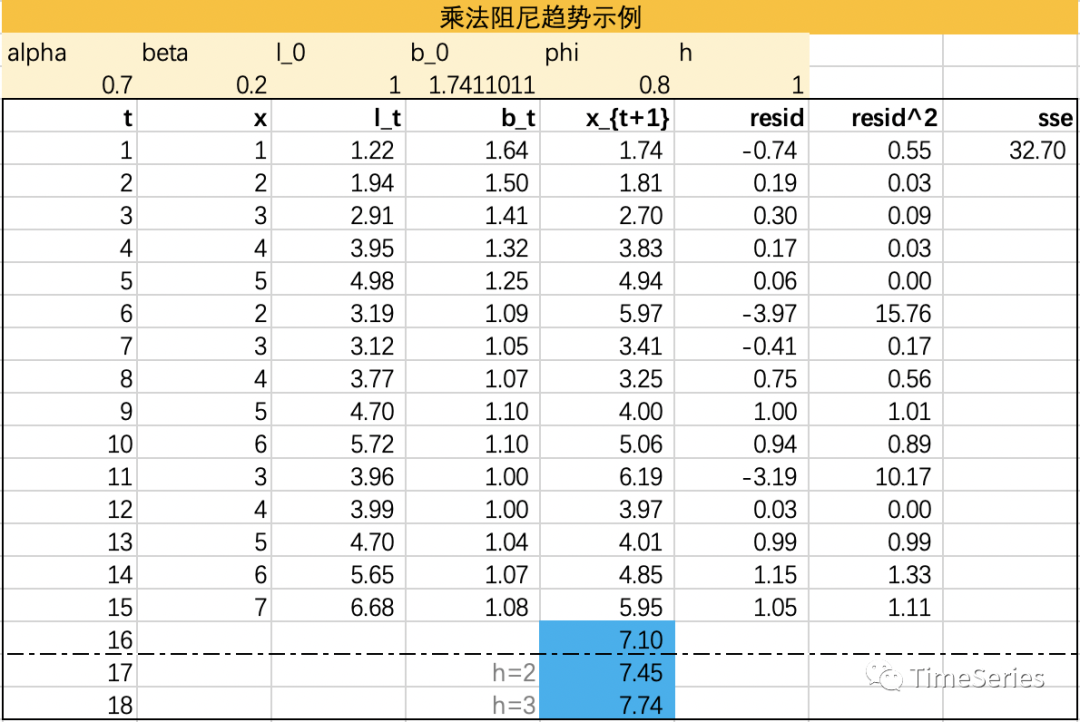
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
fit1 = Holt(data, exponential=True, damped_trend=True).fit(smoothing_level=0.7, smoothing_trend=0.2, damping_trend=0.8, optimized=False)
print(fit1.summary())
print('forecast:', fit1.forecast(3))
 三次指数平滑
三次指数平滑三次指数平滑是二次指数平滑基础上再做一次平滑,使用中通常使用Holt-Winters方法,我们平时讲三次指数平滑方法一般也是特指Holt-Winters指数平滑。
Holt (1957) 和 Winters (1960) 将Holt方法进行拓展,增加了对季节因素的处理。方法中包含一个预测方程和三个平滑方程 (一个用于水平,一个用于趋势,一个用于季节性分量)。
与趋势一样,季节性也有加性(线性)或乘性(指数)过程。当季节变化在时间序列中大致保持不变时,通常选择加法模型;而当季节变化与时间序列的水平成比例变化时,通常选择乘法模型。
Holt-Winters加法模型
用 来表示季节频率,如季度数据的m=4,月度数据的m=12。
参数1:,水平平滑参数
参数2:,趋势平滑参数
参数3:,季节性平滑参数,控制季节成分的影响
预测方程 :
水平方程 :
趋势方程 :
季节性方程:
其中,趋势方程与Holt线性方程相同。
示例演示将方程带入方程中,季节性方程也可表示为:
其中,
通常,
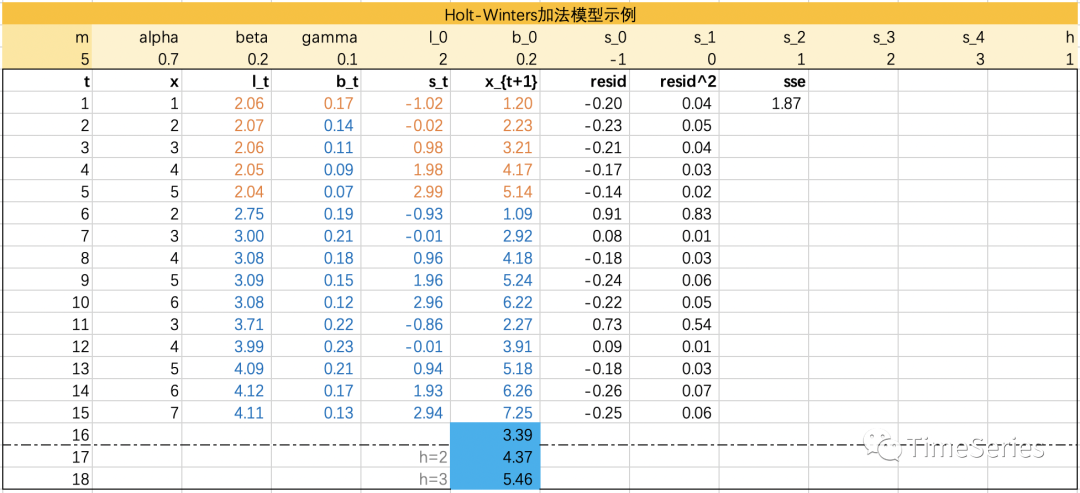
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
fit1 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='add').fit(smoothing_level=0.7, smoothing_trend=0.2, smoothing_seasonal=0.1, optimized=False)
print(fit1.summary())
print('forecast:', fit1.forecast(3))
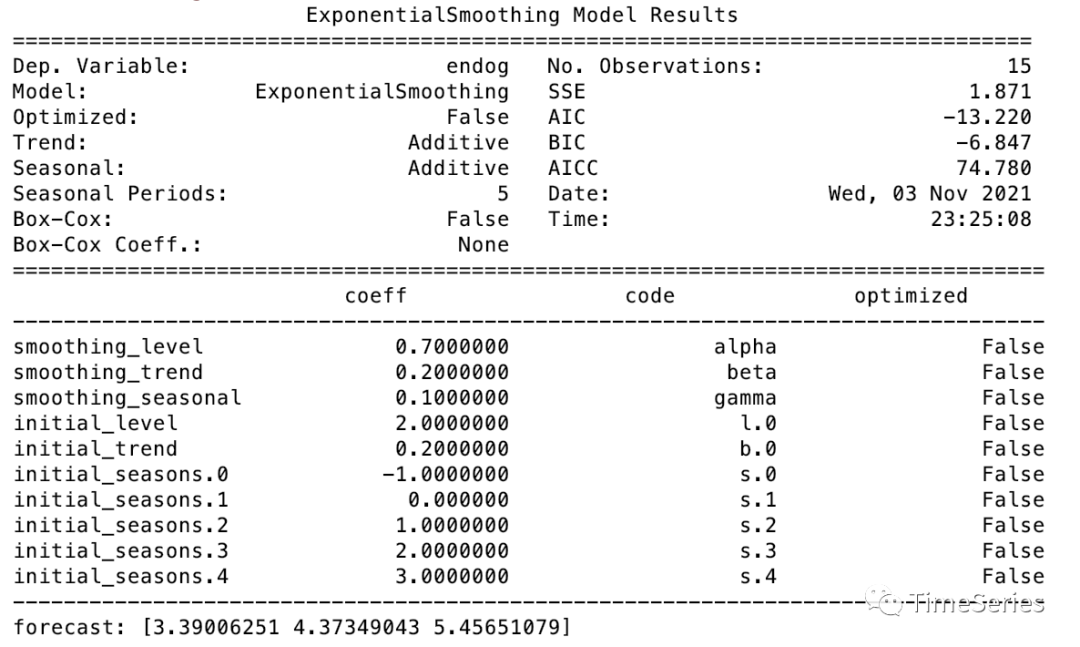
Holt-Winters乘法模型
参数1:,水平平滑参数
参数2:,趋势平滑参数
参数3:,季节性平滑参数,控制季节成分的影响
预测方程 :
水平方程 :
趋势方程 :
季节性方程:
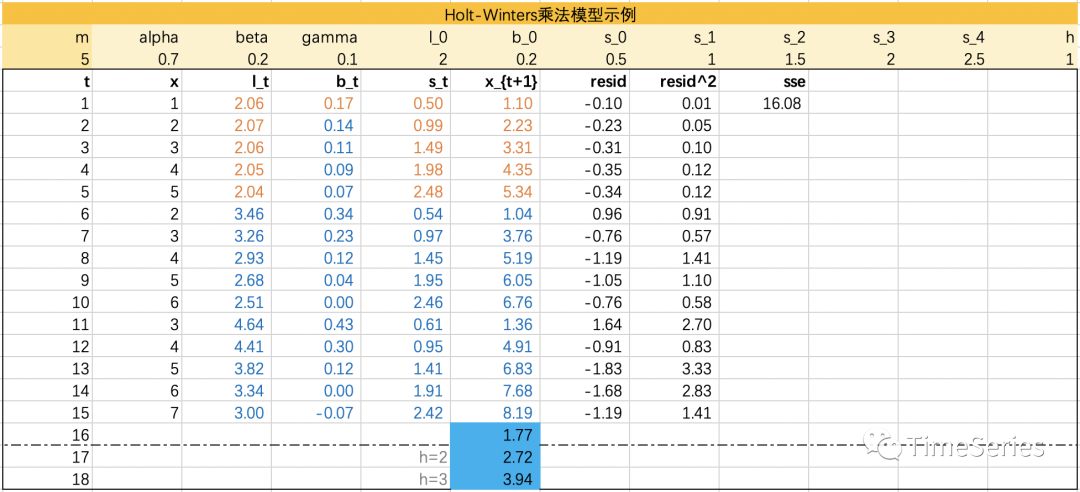
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
fit1 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='mul').fit(smoothing_level=0.7, smoothing_trend=0.2, smoothing_seasonal=0.1, optimized=False)
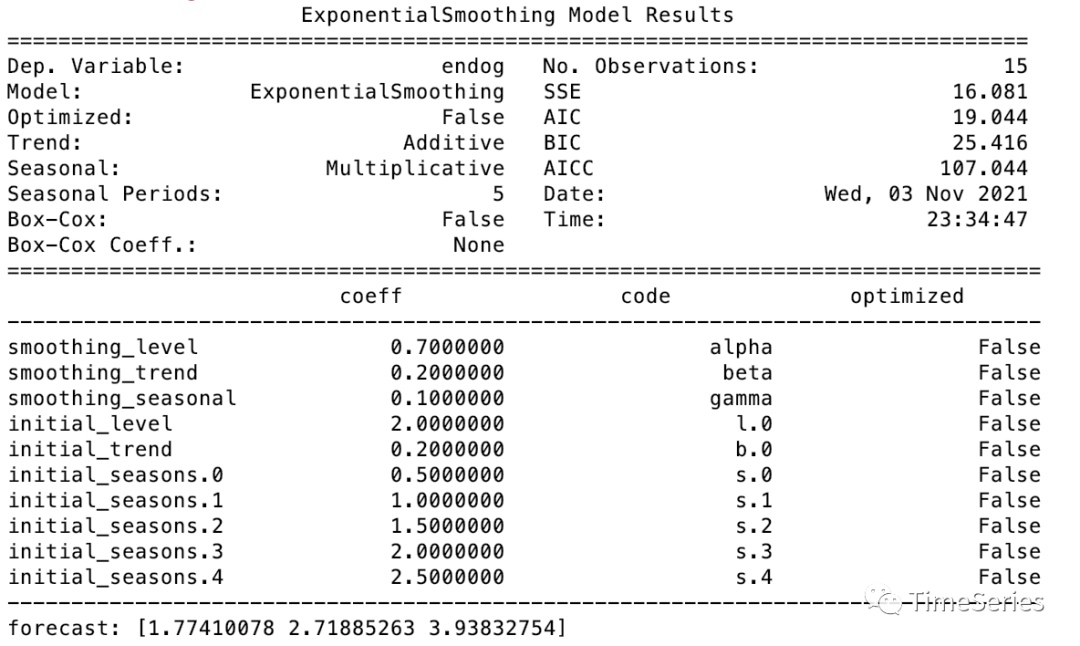
print(fit1.summary())
print('forecast:', fit1.forecast(3))
Holt-Winters的衰减法
加性和乘性Holt-Winters方法都可以进一步使用衰减法 。带有衰减趋势和乘性季节性的Holt-Winters方法通常可以为季节数据提供准确的和稳健的预测值。乘法模型增加阻尼参数的形式如下:
参数1:,水平平滑参数
参数2:,趋势平滑参数
参数3:,季节性平滑参数
参数4:,0<<1,阻尼参数
预测方程 :
水平方程 :
趋势方程 :
季节性方程:
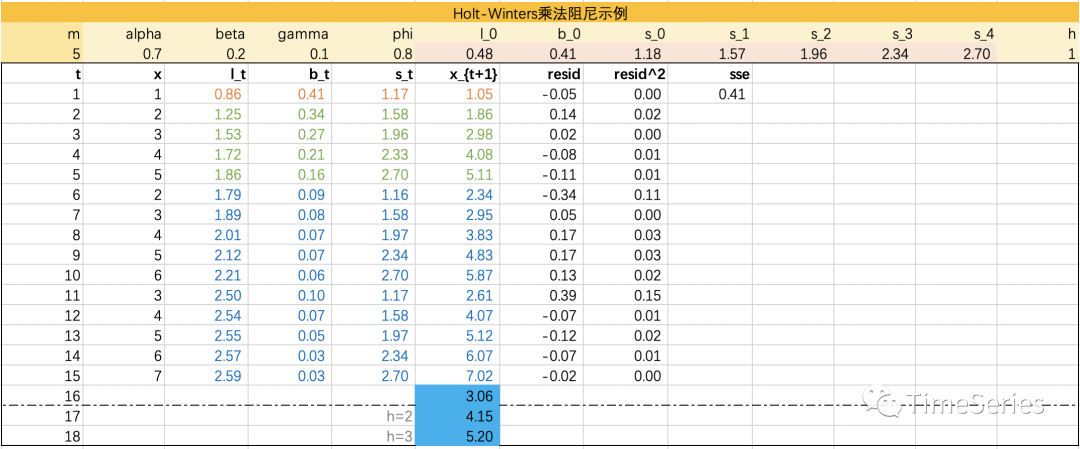
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
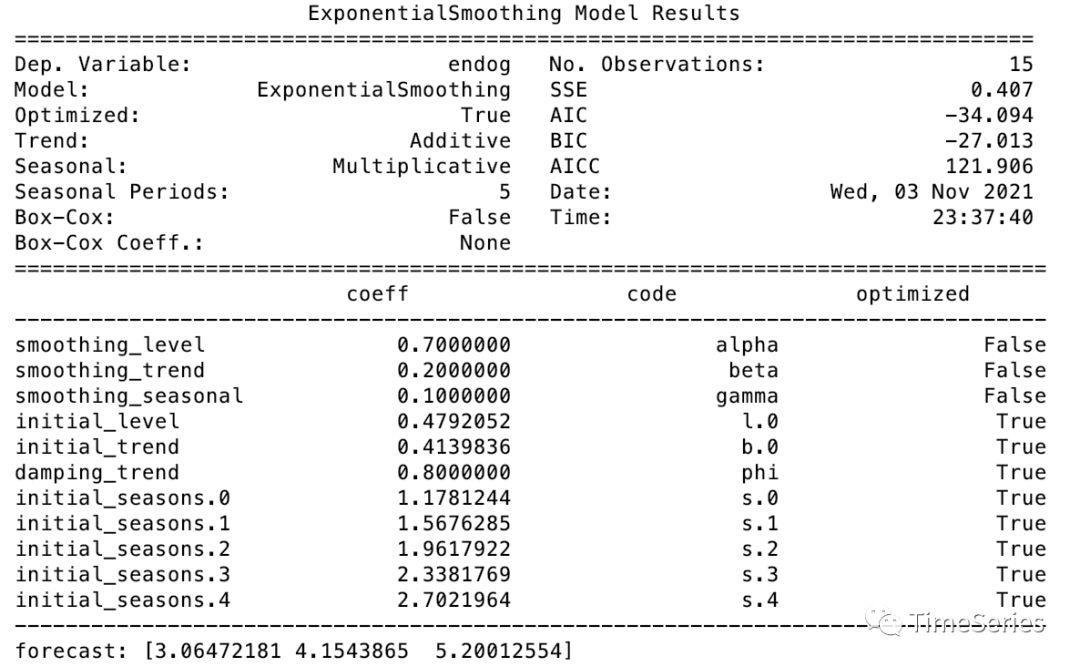
fit1 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='mul', damped_trend=True).fit(smoothing_level=0.7, smoothing_trend=0.2, smoothing_seasonal=0.1, optimized=True)
print(fit1.summary())
print('forecast:', fit1.forecast(3))
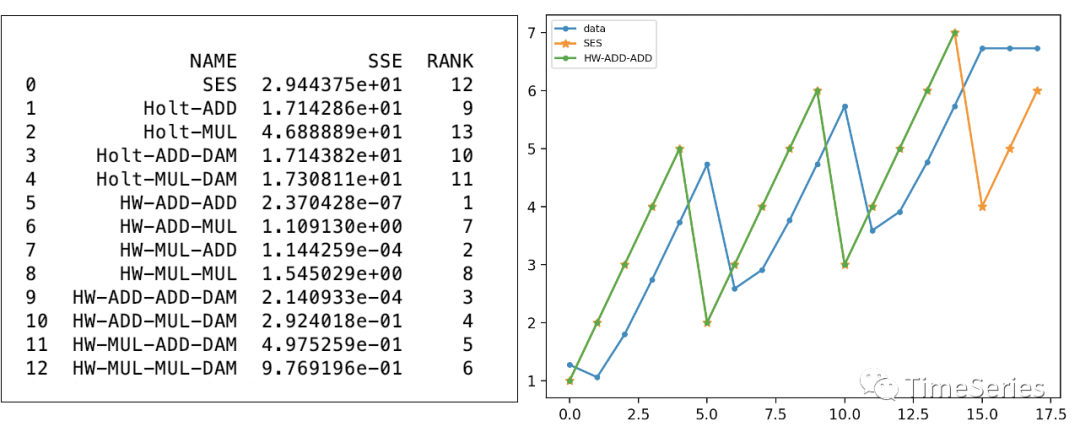
 写在最后
写在最后仍使用本次构造的简单数据,对比展示不同方法下的效果,可以看出Holt-Winters方法对当前周期性的数据拟合很好,但是需要指定周期大小,所以Holt-Winters一般适用于有明确周期性的数据。实践中一般不使用乘性趋势方法,通常效果较差。另外,statoolsmodels中fit训练时,支持对数据进行box-cox变换等处理,下面代码中不再作展示。
import numpy as np
import pandas as pd
from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt
# 数据
data = [1,2,3,4,5,2,3,4,5,6,3,4,5,6,7]
# 训练
fit1 = SimpleExpSmoothing(data).fit()
fit2 = Holt(data).fit()
fit3 = Holt(data, exponential=True).fit()
fit4 = Holt(data, exponential=False, damped_trend=True).fit()
fit5 = Holt(data, exponential=True, damped_trend=True).fit()
fit6 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='add').fit()
fit7 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='mul').fit()
fit8 = ExponentialSmoothing(data, seasonal_periods=5, trend='mul', seasonal='add').fit()
fit9 = ExponentialSmoothing(data, seasonal_periods=5, trend='mul', seasonal='mul').fit()
fit10 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='add', damped_trend=True).fit()
fit11 = ExponentialSmoothing(data, seasonal_periods=5, trend='add', seasonal='mul', damped_trend=True).fit()
fit12 = ExponentialSmoothing(data, seasonal_periods=5, trend='mul', seasonal='add', damped_trend=True).fit()
fit13 = ExponentialSmoothing(data, seasonal_periods=5, trend='mul', seasonal='mul', damped_trend=True).fit()
# 效果
FIT = [fit1, fit2, fit3, fit4, fit5, fit6, fit7, fit8, fit9, fit10, fit11, fit12, fit13]
SSE = [fit.sse for fit in FIT]
NAME = ['SES', 'Holt-ADD', 'Holt-MUL', 'Holt-ADD-DAM', 'Holt-MUL-DAM', 'HW-ADD-ADD', 'HW-ADD-MUL', 'HW-MUL-ADD', 'HW-MUL-MUL', 'HW-ADD-ADD-DAM', 'HW-ADD-MUL-DAM', 'HW-MUL-ADD-DAM', 'HW-MUL-MUL-DAM']
# 对比
df = pd.DataFrame({'NAME': NAME, 'SSE': SSE})
df['RANK'] = df['SSE'].rank().astype(int)
print(df.head(13))
# 画图
sel_index = np.argmin(SSE)
sel_model = FIT[int(sel_index)]
sel_model_name = NAME[int(sel_index)]
l1, = plt.plot(list(fit1.fittedvalues) + list(fit1.forecast(3)), marker='.')
l2, = plt.plot(list(sel_model.fittedvalues) + list(sel_model.forecast(3)), marker='*')
l3, = plt.plot(data, marker='.')
plt.legend(handles = [l1, l2, l3], labels = ['data', 'SES', sel_model_name], loc='best', prop={'size': 7})
plt.show() #plot里label顺序错了
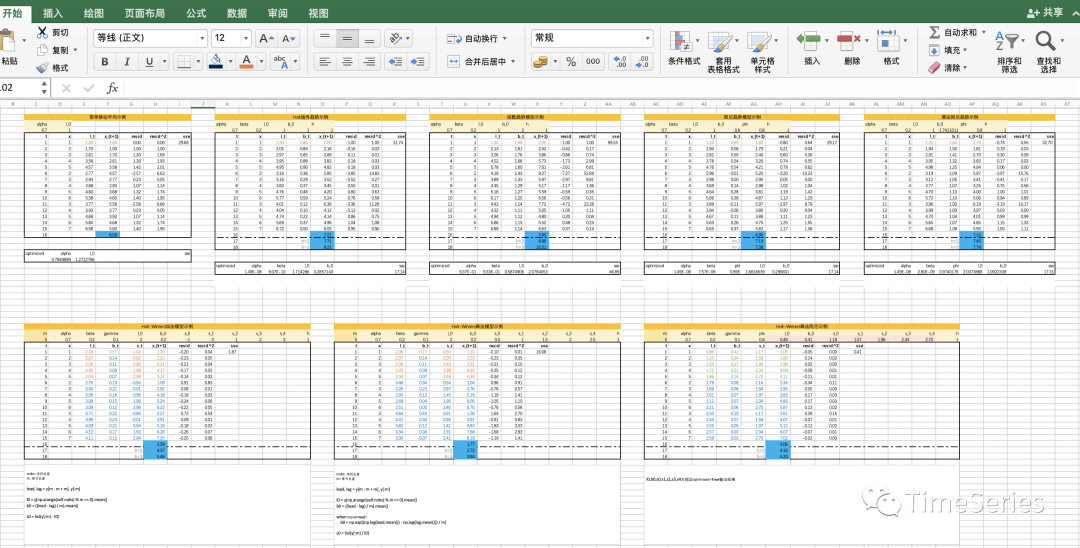
指数平滑各种版本的实现细节过于琐碎,可以后台回复关键字“ES”获取Excel示例下载地址,对于想要了解细节的朋友必会有所帮助。
 参考链接
参考链接
[1]https://www.statsmodels.org/v0.11.0/_modules/statsmodels/tsa/holtwinters.html
[2]https://otexts.com/fppcn/holt-winters.html
[3]https://wiki.mbalib.com/wiki/%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95
[4]https://www.cnblogs.com/houfei/p/13450880.html
[5]https://blog.csdn.net/fxlou/article/details/79678860
[6]https://www.cnblogs.com/21207-iHome/p/6673573.html

