不会构建依存语义图?不存在的
各位看官里面请~
如何得到一个分词在依存句法层面距离小于等于3个单位的所有分词？可能各位看官看到这个问题会有点迷糊，没事儿，让我慢慢道来。图结构就不再赘述，各位看官可以看这篇文章：
所以，我们紧随其后，构建依存关系的Graph!!!构建图的函数如下：
。各位看官自行探索叭，欢迎分享~
溜~~~
传送门：
如何得到一个分词在依存句法层面距离小于等于3个单位的所有分词？可能各位看官看到这个问题会有点迷糊，没事儿，让我慢慢道来。图结构就不再赘述，各位看官可以看这篇文章：
数据结构慕寒说，公众号：慕寒说当“Python”遇上“数据结构”不过为了解决这个问题，我们需要对基本的图结构相关的函数做一些修改，修改后的函数如下：
class Vertex:
'''
表示图中的每一个顶点
'
''
def __init__(self, index):
self.id = index
self.connectedTo = {}
self.color = 'white'
self.dist = sys.maxsize # 从起点到当前顶点的最小权重路径的总权重
self.pred = None
self.disc = 0
self.fin = 0
def addNeighbor(self, nbr, weight = 0, relation = None):
self.connectedTo[nbr] = [weight, relation]
def __str__(self):
nbrInfo = []
for nbr in self.connectedTo.keys():
nbrInfo.append([nbr.id, self.connectedTo[nbr][0], self.connectedTo[nbr][1]])
return str(nbrInfo)
def getConnections(self):
return self.connectedTo.keys()
def getId(self):
return self.id
def getWeight(self, nbr):
return self.connectedTo[nbr][0]
def getRelation(self, nbr):
return self.connectedTo[nbr][1]
def setColor(self,color):
self.color = color
def setDistance(self,d):
self.dist = d
def setPred(self,p):
self.pred = p
def setDiscovery(self,dtime):
self.disc = dtime
def setFinish(self,ftime):
self.fin = ftime
def getFinish(self):
return self.fin
def getDiscovery(self):
return self.disc
def getPred(self):
return self.pred
def getDistance(self):
return self.dist
def getColor(self):
return self.color
class Graph:
'''
图
'
''
def __init__(self):
self.vertList = {}
self.numVertices = 0
#self.count = 0
def addVertex(self, index, name):
self.numVertices = self.numVertices + 1
newVertex = Vertex(index)
self.vertList[name] = newVertex
return newVertex
def getVertex(self, n):
if n in self.vertList:
return self.vertList[n]
else:
return None
def __contains__(self, n):
return n in self.vertList
def addEdge(self, f, fIndex, t, tIndex, cost = 0, relation = None):
if f not in self.vertList:
nv = self.addVertex(fIndex, f)
if t not in self.vertList:
nv = self.addVertex(tIndex, t)
self.vertList[f].addNeighbor(self.vertList[t], cost, relation)
def getVertices(self):
return self.vertList.keys()
def __iter__(self):
return iter(self.vertList.values())
那什么是句法分析？什么是依存句法层面距离呢？这就涉及慕寒接触的自然语言处理领域了。对于文本：“台风豪雨所造成的水把市区淹得惨不忍睹。”我们可以分析它的结构信息，比如说：各个词的词性、不同词之间的逻辑关系、不同词之间的语义关系等等。这方面的内容，慕寒不说太多，因为不是本文章的关注点，我们今天关注的是算法层面。如果各位看官想要了解的话，可以后台留言，慕寒可以出文章进行说明~
我们来分析一下这个问题，既然要获得分词在依存句法层面距离小于等于3个单位的所有分词，那我们首先要获得这个文本的分词结果、依存关系！！！这个很简单，慕寒这里用的哈工大的pyltp实现，后面也用了哈工大的一些模型（如侵必删）。
完成之后，如果我们将不同分词之间依存关系画出来的话，我们可以发现，这不明显就是图结构嘛？看下图：
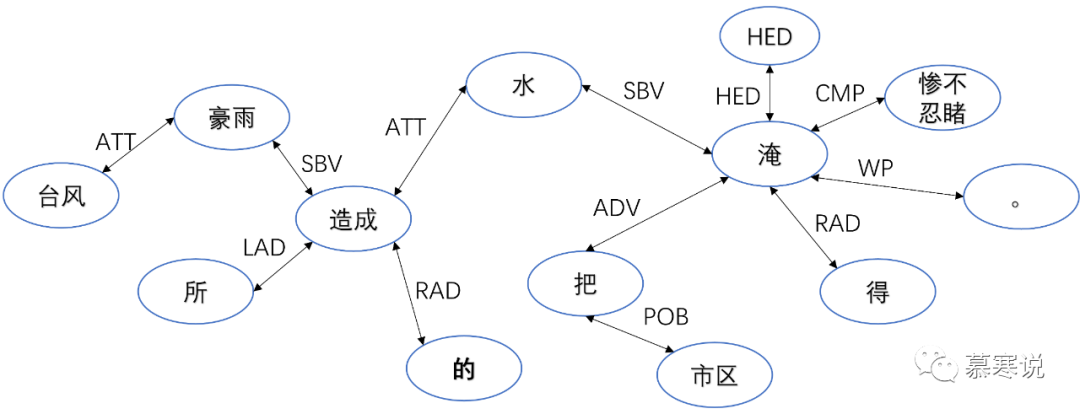
所以，我们紧随其后，构建依存关系的Graph!!!构建图的函数如下：
def buildGraph(self):
'''
构建图结构
权重距离为1个单位
'
''
for index in range(len(self.segList)):
seg = self.segList[index]
arcIndex = self.arcs[index][0] - 1
arcSeg = self.segList[arcIndex]
arcName = self.arcs[index][1]
self.Graph.addVertex(index, seg + str(index))
for index in range(len(self.segList)):
seg = self.segList[index]
arcIndex = self.arcs[index][0] - 1
arcSeg = self.segList[arcIndex]
arcName = self.arcs[index][1]
self.Graph.addEdge(seg + str(index), index, arcSeg + str(arcIndex), arcIndex, 1, arcName)
self.Graph.addEdge(arcSeg + str(arcIndex), arcIndex, seg + str(index), index, 1, arcName)
各位客官会发现，这个图节点的名字的格式为：分词+索引。为啥呢？因为这里图结构采用字典的键值对表示的，我们都知道字典中不能存在同样的键，所以慕寒就用这个分词在分词列表中的索引信息来表示键了。
那么问题来了，我怎么获得依存句法层面距离小于等于3个单位的所有分词呢？（为了方便期间，这个距离慕寒就说成：依存距离）这里我们需要引入一个权重的概念，慕寒想的是：既然只考虑单位距离，那就可以让每个相邻的分词之间的距离权重为1。当然了，我们要默认各分词一开始是不相邻的，所以距离设置成很大很大（代码实现为：sys.maxsize）。那么如何找到依存距离小于等于3的所有分词呢？通过对图相关算法的回顾，慕寒发现了Dijkstra算法，没错！就是解决最短路径的Dijkstra算法。各位看官是不是突然明白了这个问题该如何解决呢？有了各节点之间的最短路径，那么我们就只需要把最短路径小于等于3个单位的分词找出来，那不就大功告成了！！！Dijkstra函数如下：
def dijkstra(self, aGraph, start):
pq = PriorityQueue()
start.setDistance(0) # 将start节点到start节点的距离设置为0
pq.buildHeap([(v.getDistance(), v) for v in aGraph])
while not pq.isEmpty():
currentVert = pq.delMin()
#print("currentVert:",currentVert)
#print("pq:\n", pq.heapArray)
for nextVert in currentVert.getConnections():
newDist = currentVert.getDistance() + currentVert.getWeight(nextVert)
if newDist < nextVert.getDistance():
nextVert.setDistance(newDist)
nextVert.setPred(currentVert)
pq.decreaseKey(nextVert, newDist)
return pq, aGraph
当然，为了实现这个算法，我们还需要引入“优先级队列”，这可以在Python的第三方库“pythonds”导入，具体的各位看官可以看慕寒最后附上的所有代码链接~。通过Dijkstra算法，我们就可以对原始的Graph进行修正，并用于后续的引用。
所以具体怎么用呢？别急，慕寒这里给出了使用的函数：
def getNArc(self, arcLen):
'''
获取语义逻辑arcLen内所有分词的索引
'''
segArcLenL = []
for index in range(len(self.segList)):
segArcLenL.append([])
seg = self.segList[index]
aGraph = self.Graph
start = self.Graph.getVertex(seg + str(index))
pq, newAGraph = self.dijkstra(aGraph, start)
vertexConnectArcLenIndexL = []
for vertex in newAGraph:
vertexConnectIndexL = [v.id for v in list(vertex.getConnections())]
shortDistanceL = []
for nextV in vertex.getConnections():
shortDistanceL.append(nextV.getDistance())
for vertexIndex in range(len(vertexConnectIndexL)):
vertexConnectIndex = vertexConnectIndexL[vertexIndex]
shortDistance = shortDistanceL[vertexIndex]
if (vertexConnectIndex >= 0) and (vertexConnectIndex != index) and (shortDistance > 0 and shortDistance <= arcLen):
vertexConnectArcLenIndexL.append(vertexConnectIndex)
vertexConnectArcLenIndexL = list(set(vertexConnectArcLenIndexL))
vertexConnectArcLenIndexL.sort()
segArcLenL[-1] = segArcLenL[-1] + vertexConnectArcLenIndexL
vertexConnectArcLenIndexL = []
self.buildGraph()
return segArcLenL
大致思路就是：对于每个分词seg，我们要通过Dijkstra算法对文本依存句法分析得到的Graph进行修正后的newGraph，该图中各节点之间的距离为节点之间最短路径。然后再根据分词seg得到newGraph中所有与该seg的最短路径小于等于3的节点（我们需要的分词）以及其在分词列表中的索引位置，最终的输出如下：
。各位看官自行探索叭，欢迎分享~
溜~~~
传送门：
链接：
https://pan.baidu.com/s/1mYiiK-3ngYvY_wBbXhlTEg 提取码： 1105评论