如何看待李沐老师提出的「用随机梯度下降来优化人生」？-技术圈

来源：知乎

电光幻影炼金术（上海交大计算机第一名）回答：

看完李沐老师的文章，深受启发。本人阅读大量文献，提出了下面“反向利用随机梯度下降优化人生“的方案。下文与李沐老师的文章的原文（在引用块里）一一对应进行回答。

李沐：目标要大。不管是人生目标还是目标函数，你最好不要知道最后可以走到哪里。如果你知道，那么你的目标就太简单了，可能是个凸函数。你可以在一开始的时候给自己一些小目标，例如期末考个80分，训练一个线性模型。但接下来得有更大的目标，财富自由也好，100亿参数的变形金刚也好，得足够一颗赛艇。

反向：目标要小而具体。如果目标过大，很容易导致因为噪声过大，奖励过于稀疏而发散^[1]。收敛情况很好的，往往是图片分类这种目标非常明确而具体的任务。与之相反，在真实机器人面临的搜索空间很大的场景，随机梯度下降很容易发散^[2]。

李沐：坚持走。不管你的目标多复杂，随机梯度下降都是最简单的。每一次你找一个大概还行的方向（梯度），然后迈一步（下降）。两个核心要素是方向和步子的长短。但最重要的是你得一直走下去，能多走几步就多走几步。

反向：该放弃时就要放弃。一个简单也很有效的解决梯度策略发散的技巧就是抛弃过大的梯度^[3]。如果遇到很大的梯度还不选择抛弃或者裁剪，很容易会导致发散的结果。除此之外，很多场合使用随机梯度下降训练几个epoch会发现梯度越来越大，这时候一定要及时停下来检查数据。不然一晚上过后只能得到一个NAN（发散)的结果，白白浪费宝贵的算力资源。

李沐：痛苦的卷。每一步里你都在试图改变你自己或者你的模型参数。改变带来痛苦。但没有改变就没有进步。你过得很痛苦不代表在朝着目标走，因为你可能走反了。但过得很舒服那一定在原地踏步。需要时刻跟自己作对。

反向：拒绝内卷。优化有两种模式，一种很陡峭曲折的（比较艰难，对应内卷），一种是比较平滑的（比较轻松，对应佛系和不卷）。这里我引用一篇顶会论文中^[4]的可视化结果，

上图左边的（a)优化曲面不平滑，对应很内卷的残酷场景；右边的（b）是很平滑的过程，对应不内卷的自由发展。那么究竟是(a)好呢，还是(b)好呢？想必大家已经猜到了，(b)这种优化模式要远远好于(a)，错误率小两倍多（错误率：(b)5.89%，(a)13.31%）。因此，大家一定要学会拒绝内卷，保护自己平滑的成长过程。

李沐： 四处看看。每一步走的方向是你对世界的认识。如果你探索的世界不怎么变化，那么要么你的目标太简单，要么你困在你的舒适区了。随机梯度下降的第一个词是随机，就是你需要四处走走，看过很多地方，做些错误的决定，这样你可以在前期迈过一些不是很好的舒适区。

反向：别走太远。正则化是深度学习乃至机器学习中非常常见的技巧，要想取得好的收敛效果，往往需要加以约束，不能走得太远^[3]。放任自我也会容易导致发散。

李沐： 赢在起点。起点当然重要。如果你在终点附近起步，可以少走很多路。而且终点附近的路都比较平，走着舒服。当你发现别人不如你的时候，看看自己站在哪里。可能你就是运气很好，赢在了起跑线。如果你跟别人在同一起跑线，不见得你能做更好。

反向：起点不重要。Facebook公司Kaiming大神的一篇论文^[5]用大量实验事实证明，接受预训练的模型，虽然一开始会好一些，但是后面跟随机初始化的模型相差无几。有实验结果图为证：

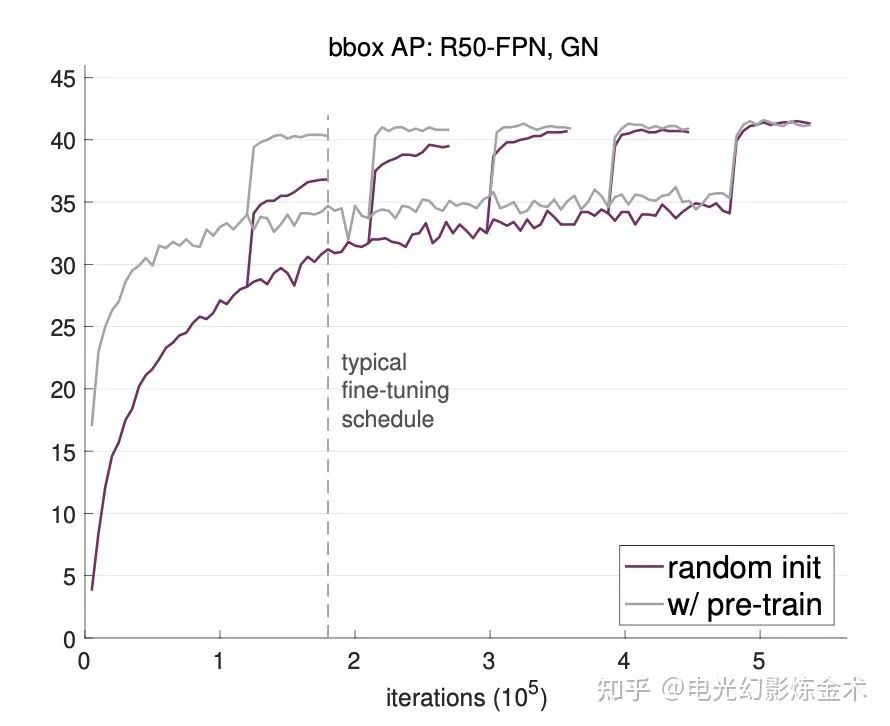
李沐： 很远也能到达。如果你是在随机起点，那么做好准备前面的路会非常不平坦。越远离终点，越人迹罕见。四处都是悬崖。但随机梯度下降告诉我们，不管起点在哪里，最后得到的解都差不多。当然这个前提是你得一直按照梯度的方向走下去。如果中间梯度炸掉了，那么你随机一个起点，调整步子节奏，重新来。

反向：太远就到不了了。如果间隔时间太长，奖励函数的折损会非常严重，导致强化学习的成功率不高。这也是强化学习目前只能在模拟器中成功（无法在真实的机器人上被广泛应用）的主要原因之一。

李沐：简单最好。当然有比随机梯度下降更复杂的算法。他们想每一步看想更远更准，想步子迈最大。但如果你的目标很复杂，简单的随机梯度下降反而效果最好。深度学习里大家都用它。关注当前，每次抬头瞄一眼世界，快速做个决定，然后迈一小步。小步快跑。只要你有目标，不要停，就能到达。

反向：越结构化的模型越好。文献显示^[6]，拓扑结构较复杂的模型，在同样的梯度下降算法之后会产生更小的泛化误差。而过于简单的模型，往往会容易收敛到平凡解，丧失足够的泛化能力。

不是很懂优化这块，欢迎批评指点。

有些点没讲到，是因为找不到特别好的文献，或者读起来没那么有趣。

如果要我说，人生反正不是监督学习，更像是强化学习甚至无监督学习。

当然，也可能人生就是随机挑战。

Towser回答：

然而，除了优化算法还有初始化：有些人有预训练模型，一出生就在最优点附近，随便走两步就比大多数人吭哧吭哧走半天效果还好；有些人出生在悬崖边上，一步走错就万劫不复。

然而，除了优化算法还有损失函数：有些人的损失函数是强凸的，优化的方向非常明确，或者是有很强的正则项，走错的时候可以把他往回拉；有些人的损失函数数值极其不稳定，动不动就爆 NaN/Inf。

就算是优化算法，也要看你能拿到什么信息：有些人是一阶优化，跟着梯度信息慢慢往前走；有些人是零阶优化，拿不到梯度信息，就只能自己摸黑瞎走走。

参考

^Hare, Joshua. "Dealing with sparse rewards in reinforcement learning." arXiv preprint arXiv:1910.09281 (2019).
^Peters, Jan, and Stefan Schaal. "Policy gradient methods for robotics." 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2006.
^^a^bSchulman, John, et al. "Proximal policy optimization algorithms." arXiv preprint arXiv:1707.06347 (2017).
^Li, Hao, et al. "Visualizing the loss landscape of neural nets." arXiv preprint arXiv:1712.09913 (2017).
^He, Kaiming, Ross Girshick, and Piotr Dollár. "Rethinking imagenet pre-training." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019.
^Corneanu, Ciprian A., Sergio Escalera, and Aleix M. Martinez. "Computing the testing error without a testing set." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.

——The End——

为了方便大家学习，我们建立微信交流群，欢迎大家加我的微信，邀你进群！

微商无关人员勿扰！