每日一题 | Python3 实现「208. 实现 Trie(前缀树)」
208. 实现 Trie (前缀树)
题目链接
https://leetcode-cn.com/problems/implement-trie-prefix-tree/
也可以点击「阅读原文」直达题目链接。
题目描述
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie()初始化前缀树对象。void insert(String word)向前缀树中插入字符串word。boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例 :
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示:
1 <= word.length, prefix.length <= 2000word和prefix仅由小写英文字母组成insert、search和startsWith调用次数 总计 不超过 次
解题思路
这道题考查的是前缀树的思想。
前缀树在实际的工程应用中有着很大的应用。很常见的包括搜索引擎的关键词提示功能,以及 IDE 的自动补全功能等等...
Trie 树的本质是将重复的前缀子串进行合并的思想,也就是说如果一个字符出现了多次,但是只需要存储一次就可以了。
刚开始的时候,Trie 树是一颗空树,Trie 树的构造过程就是相当于往 Trie 树中插入字符串,当字符串插入完毕后,Trie 树就构造完成了。
这里我找了一个 Trie 构造过程,你可以看下。假定要插入的字符串一共有 6 个,分别是"how", "hi", "her", "hello", "so", "see"。红色节点表示一个字符串的结尾。
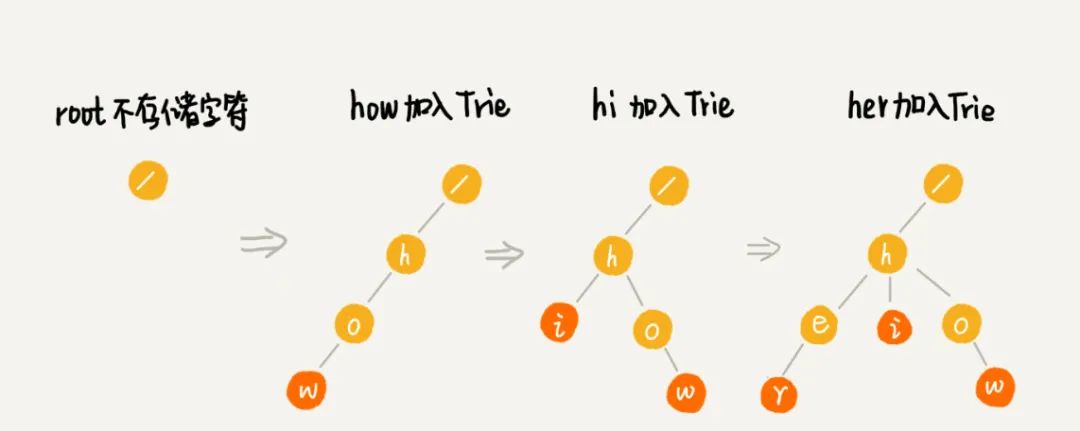
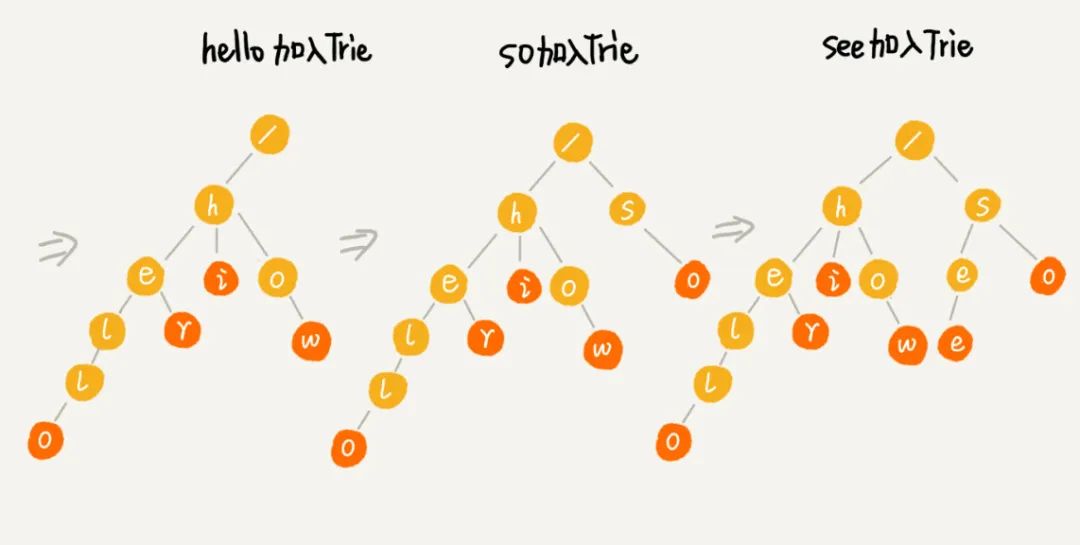
那么应该如何实现呢?因为题目中我们假定字符串只包含小写字母。因为小写字母一共有 26 个,仿照二叉树的存储方式,我们可以使用一个大小为 26 的数组来存储其孩子节点。另外,对于每一个节点,还需要一个额外的变量来记录此节点代表的字符是否是一个字符串的结尾,为 True 的话代表着图中的红色节点。
另外呢,因为数组有天然的支持下标索引的特性,因此我们甚至可以不存储节点存储的数据,因为在进行查找的时候,直接通过字符 ASCII 码的相对值作为访问孩子数组的下标即可。
Python3 代码
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self._children = [None] * 26
self._is_ending_char = False
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
root = self
for index, char in map(lambda x: (ord(x) - ord("a"), x), word):
if not root._children[index]:
root._children[index] = Trie()
root = root._children[index]
root._is_ending_char = True
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
root = self
for index in map(lambda x: ord(x) - ord("a"), word):
if not root._children[index]:
return False
root = root._children[index]
return root._is_ending_char
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
root = self
for index in map(lambda x: ord(x) - ord("a"), prefix):
if not root._children[index]:
return False
root = root._children[index]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
复杂度分析:
时间复杂度:
空间复杂度:
其中 n 为要插入字符串的总长度,k 为查询字符串的长度。也就是说,Trie 树构造完成后,查询的时间复杂度只和要查询字符串的长度有关,而构造 Trie 树,也就是插入的时候,时间复杂度是所有要插入的字符串的长度之和。
总结
虽然 Trie 树的思想是合并重复的前缀子串,看上去节省了存储空间,但实际上 Trie 树利用的是空间换时间的思想,因为每个节点需要一个孩子数组,用于指向下一层的地址。在字符的范围很大的时候,比如说不仅仅只有英文小写字母的时候,光存储 孩子数组就需要浪费很多的存储空间。如果再考虑中文的话,所耗费的空间就更大了。
因此,Trie 树有很多可以优化的地方,比如说缩点优化,感兴趣的可以自己下去搜索下。还有一个常见的方法就是孩子数组利用有序数组来进行实现,不用事先申请全部字符所占的空间,遇到不存在的字符时,将其插入到其应该所在的位置即可。
好了,今天的内容就到这里了。我最近在学习数据结构与算法的相关知识,也会在力扣进行每日一题的打卡。如果你最近在求职面试或者也在进行力扣进行每日一题的打卡的话,欢迎加入我们,后台回复「加群」即可。我一直坚信一个人走的更快,一群人走的更远。很多时候,只要坚持下去了,那么你就超越了很多人。
参考资料:
https://time.geekbang.org/column/article/72414 https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/yu-ni-yi-qi-xue-suan-fa-python3-shi-xian-p0fr/
