最全解密微信红包随机算法(含代码实现)
1、引言
一方面是各社交/IM产品中的红包功能同质化严重,红包算法的“可玩性”便是“核心竞争力所在”,这是同质化功能的差异化竞争思路,不会随便公开。
另一方面,市场上还存在各种抢红包插件这类灰产存在,一旦公开这些算法,很可能又被这帮插件开发者们搞出什么幺蛾子。
所以,这样的情况下,如果要做社交/IM产品中的红包功能,红包随便算法该怎么实现,基本上只能自已琢磨,很难找到大厂算法直接套用。
本着即时通讯网一贯的im知识传播精神,我收集整理并参考了大量的网上资料,综合了比较靠谱的信息来源,便有了本文。本文根据有限的资料,分享了微信红包随机算法实现中的一些技术要点,并整理了两种比较靠谱的红包算法实现思路(含可运行的实现代码),希望能给你的红包算法开发带来启发。
申明:本文资料整理自网络,仅供学习研究之用,如有不妥,请通知Jack Jiang。
2、系列文章
《社交软件红包技术解密(一):全面解密QQ红包技术方案——架构、技术实现等》 《社交软件红包技术解密(二):解密微信摇一摇红包从0到1的技术演进》 《社交软件红包技术解密(三):微信摇一摇红包雨背后的技术细节》 《社交软件红包技术解密(四):微信红包系统是如何应对高并发的》 《社交软件红包技术解密(五):微信红包系统是如何实现高可用性的》 《社交软件红包技术解密(六):微信红包系统的存储层架构演进实践》 《社交软件红包技术解密(七):支付宝红包的海量高并发技术实践》 《社交软件红包技术解密(八):全面解密微博红包技术方案》 《社交软件红包技术解密(九):谈谈手Q春节红包的设计、容灾、运维、架构等》 《社交软件红包技术解密(十):手Q客户端针对2020年春节红包的技术实践》 《社交软件红包技术解密(十一):解密微信红包随机算法(含演示代码)》(* 本文)
3、微信红包算法要点汇总
资料来源:来自InfoQ的某架构群的技术讨论,由朱玉华整理(个人博客是:zhuyuhua.com(目前已无法访问))。
资料背景:起因是有朋友在朋友圈咨询微信红包的架构,于是在微信团队成员参与讨论的情况下,我(指“朱玉华”)整理了这次讨论的技术要点,也就是下面的内容(内容为问答形式)。
3.1、算法实现的技术要点
问:微信的金额什么时候算?
答:微信金额是拆的时候实时算出来,不是预先分配的,采用的是纯内存计算,不需要预算空间存储。
为什么采取实时计算金额?原因是:实时效率更高,预算才效率低下。预算还要占额外存储。因为红包只占一条记录而且有效期就几天,所以不需要多大空间。就算压力大时,水平扩展机器是。
问:关于实时实时性,为什么明明抢到红包,点开后发现没有?
答:2014年的红包一点开就知道金额,分两次操作,先抢到金额,然后再转账。
2015年的红包的拆和抢是分离的,需要点两次,因此会出现抢到红包了,但点开后告知红包已经被领完的状况。进入到第一个页面不代表抢到,只表示当时红包还有。
问:关于分配算法,红包里的金额怎么算?为什么出现各个红包金额相差很大?
答:随机,额度在 0.01 和剩余平均值 2 之间。例如:发 100 块钱,总共 10 个红包,那么平均值是 10 块钱一个,那么发出来的红包的额度在 0.01元~20元之间波动。
当前面 3 个红包总共被领了 40 块钱时,剩下 60 块钱,总共 7 个红包,那么这 7 个红包的额度在:0.01~(60/72)=17.14之间。
注意:这里的算法是每被抢一个后,剩下的会再次执行上面的这样的算法(Tim老师也觉得上述算法太复杂,不知基于什么样的考虑)。
如果前面的人手气不好,那么后面的余额越多,红包额度也就越多,因此实际概率一样的。
问:红包的设计
答:微信从财付通拉取金额数据过来,生成个数/红包类型/金额放到redis集群里,app端将红包ID的请求放入请求队列中,如果发现超过红包的个数,直接返回。根据红包的逻辑处理成功得到令牌请求,则由财付通进行一致性调用,通过像比特币一样,两边保存交易记录,交易后交给第三方服务审计,如果交易过程中出现不一致就强制回归。
问:并发性处理:红包如何计算被抢完?
答:cache会抵抗无效请求,将无效的请求过滤掉,实际进入到后台的量不大。cache记录红包个数,原子操作进行个数递减,到 0 表示被抢光。财付通按照 20万笔每秒入账准备,但实际还不到 8万每秒。
问:通如何保持8w每秒的写入?
答:多主sharding,水平扩展机器。
问:数据容量多少?
答:一个红包只占一条记录,有效期只有几天,因此不需要太多空间。
问:查询红包分配,压力大不?
答:抢到红包的人数和红包都在一条cache记录上,没有太大的查询压力。
问:一个红包一个队列?
答:没有队列,一个红包一条数据,数据上有一个计数器字段。
问:有没有从数据上证明每个红包的概率是不是均等?
答:不是绝对均等,就是一个简单的拍脑袋算法。
问:拍脑袋算法,会不会出现两个最佳?
答:会出现金额一样的,但是手气最佳只有一个,先抢到的那个最佳。
问:每领一个红包就更新数据么?
答:每抢到一个红包,就cas更新剩余金额和红包个数。
问:红包如何入库入账?
答:数据库会累加已经领取的个数与金额,插入一条领取记录。入账则是后台异步操作。
问:入帐出错怎么办?比如红包个数没了,但余额还有?
答:最后会有一个take all操作。另外还有一个对账来保障。
问:既然在抢的时候有原子减了就不应该出现抢到了拆开没有的情况?
答:这里的原子减并不是真正意义上的原子操作,是Cache层提供的CAS,通过比较版本号不断尝试。
问:cache和db挂了怎么办?
答:主备 +对账。
问:为什么要分离抢和拆?
答:总思路是设置多层过滤网,层层筛选,层层减少流量和压力。
这个设计最初是因为抢操作是业务层,拆是入账操作,一个操作太重了,而且中断率高。从接口层面看,第一个接口纯缓存操作,搞压能力强,一个简单查询Cache挡住了绝大部分用户,做了第一道筛选,所以大部分人会看到已经抢完了的提示。
问:抢到红包后再发红包或者提现,这里有什么策略吗?
答:大额优先入账策略。
针对上面的技术要点,有人还画了张原理图(这是网上能找到的相对清晰的版本):

3.2、微信抢红包的过程模拟
3.2.1)发红包后台操作:
1)在数据库中增加一条红包记录,存储到CKV,设置过期时间; 2)在Cache(可能是腾讯内部kv数据库,基于内存,有落地,有内核态网络处理模块,以内核模块形式提供服务))中增加一条记录,存储抢红包的人数N。
3.2.2)抢红包后台操作:
1)抢红包分为抢和拆:抢操作在Cache层完成,通过原子减操作进行红包数递减,到0就说明抢光了,最终实际进入后台拆操作的量不大,通过操作的分离将无效请求直接挡在Cache层外面。
这里的原子减操作并不是真正意义上的原子减操作,是其Cache层提供的CAS,通过比较版本号不断尝试,存在一定程度上的冲突,冲突的用户会放行,让其进入下一步拆的操作,这也解释了为啥有用户抢到了拆开发现领完了的情况。
2)拆红包在数据库完成:通过数据库的事务操作累加已经领取的个数和金额,插入一条领取流水,入账为异步操作,这也解释了为啥在春节期间红包领取后在余额中看不到。
拆的时候会实时计算金额,其金额为1分到剩余平均值2倍之间随机数,一个总金额为M元的红包,最大的红包为 M * 2 /N(且不会超过M),当拆了红包后会更新剩余金额和个数。财付通按20万笔每秒入账准备,实际只到8万每秒。
4、微信红包算法模拟实现1(含代码)
4.1、算法约定
即:金额随机,额度在0.01和剩余平均值*2之间。(参见上一节的 “关于分配算法,红包里的金额怎么算?为什么出现各个红包金额相差很大?” 内容)
4.2、代码实现
public static double getRandomMoney(RedPackage _redPackage) {// remainSize 剩余的红包数量// remainMoney 剩余的钱if (_redPackage.remainSize == 1) {_redPackage.remainSize--;return (double) Math.round(_redPackage.remainMoney * 100) / 100;}Random r = new Random();double min = 0.01; //double max = _redPackage.remainMoney / _redPackage.remainSize * 2;double money = r.nextDouble() * max;money = money <= min ? 0.01: money;money = Math.floor(money * 100) / 100;_redPackage.remainSize--;_redPackage.remainMoney -= money;return money;}
class RedPackage {int remainSize;double remainMoney;}
static void init() {redPackage.remainSize = 30;redPackage.remainMoney = 500;}
(附件下载:http://www.52im.net/thread-3125-1-1.html)
4.3、测试结果
4.3.1单次测试
按上述代码中的初始化数据(30人抢500块),执行了两次,结果如下:
// 第一次15.69 21.18 24.11 30.85 0.74 20.85 2.96 13.43 11.12 24.87 1.86 19.62 5.97 29.33 3.05 26.94 18.69 34.47 9.4 29.83 5.17 24.67 17.09 29.96 6.77 5.79 0.34 23.89 40.44 0.92// 第二次10.44 18.01 17.01 21.07 11.87 4.78 30.14 32.05 16.68 20.34 12.94 27.98 9.31 17.97 12.93 28.75 12.1 12.77 7.54 10.87 4.16 25.36 26.89 5.73 11.59 23.91 17.77 15.85 23.42 9.77
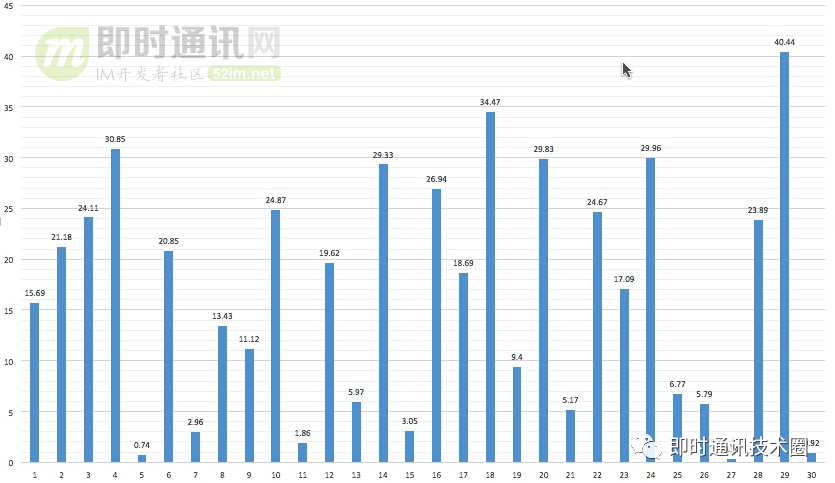
第二次随机红包数据图表如下:
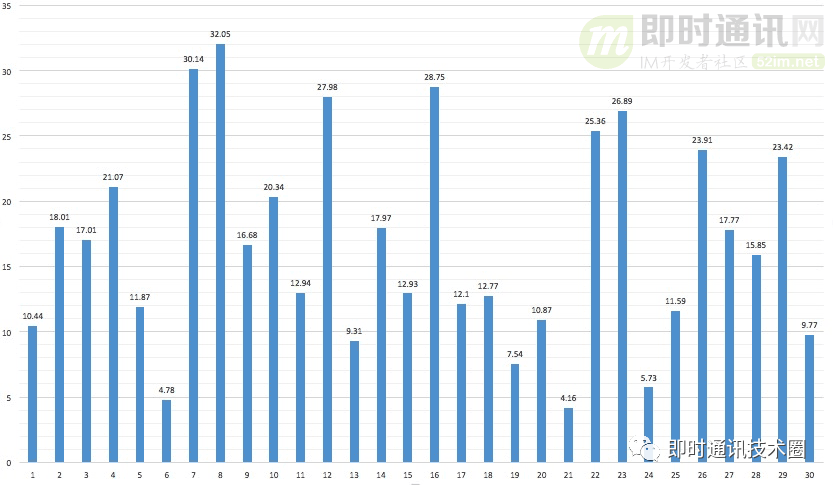
4.3.2多次均值
重复执行200次的均值:
▲ x轴为抢的顺序,y轴为该次抢到金额的概率均值
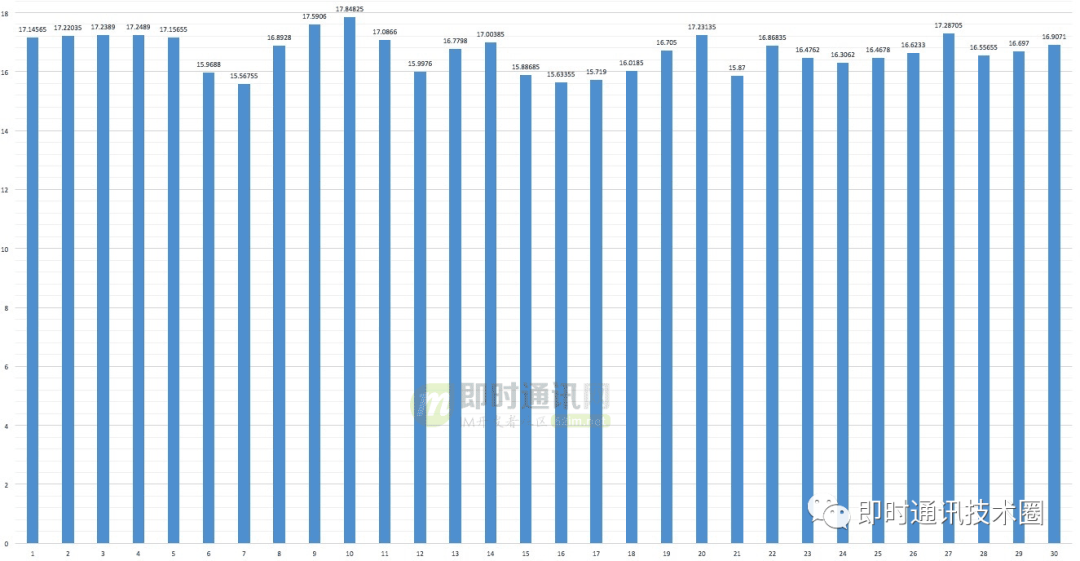
重复执行2000次的均值:

▲ x轴为抢的顺序,y轴为该次抢到金额的概率均值
从以上两张图的均值结果可以看出,这个算法中每一次能抢到的金额几率几乎是均等的,从随机性来说比较合理。
5、微信红包算法模拟实现2(含代码)
5.1、代码实现
那基于这个思想,可以写出一个红包分配算法:
/*** 并不完美的红包算法*/public static double rand(double money, int people, Listl) { if (people == 1) {double red = Math.round(money * 100) / 100.0;l.add(red);return 0;}Random random = new Random();double min = 0.01;double max = money / people * 2.0;double red = random.nextDouble() * max;red = red <= min ? min : red;red = Math.floor(red * 100) / 100.0;l.add(red);double remain = Math.round((money - red) * 100) / 100.0;return remain;}
5.2、第一次分析
可以得出如下结果:

从上图中可以很轻易的看出来,越后抢的人,风险越大,同时收益也越大,有较大几率获得“手气最佳”。
那红包面值的分布性如何呢?

从上图可以看出,都是比较接近平均值(3 元)的。
那重复 1000 次呢?

更接近了。。。
可以看出,这个算法可以让大家抢到红包面额在概率上是大致均等的。
5.3、不足之处
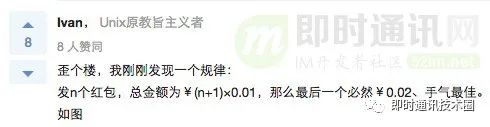
他接下来放了好几张他试验的截图。我这里取了一张,如果有兴趣,可以去知乎的问题里查看更多图片。

而此时,我哥们在和我的在讨论中,也告诉我,确实存在某个规律,可能让最后一个抢的人占有某些微小的优势,比如,多 0.01 的之类。
例如发 6 个,总额 0.09 的包,最后一个抢的有极大概率是 0.03。

然而我之前的代码却没办法体现出这一点。
比如 10 人拆 0.11 元的包,我的结果是:
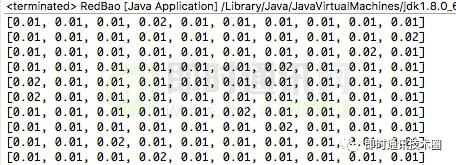
可见以上代码还存在不足之处。
于是我就有一个猜测:
这个猜测或许可以解开那位知友和我哥们这边的疑惑。
5.4、完善算法
public static double rand(double money, int people, Listl) { if (people == 1) {double red = Math.round(money * 100) / 100.0;l.add(red+0.01);return 0;}Random random = new Random();double min = 0;double max = money / people * 2.0;double red = random.nextDouble() * max;red = red <= min ? min : red;red = Math.floor(red * 100) / 100.0;l.add(red+0.01);double remain = Math.round((money - red) * 100) / 100.0;return remain;}
_money = _money - people * 0.01;
5.5、第二次分析
5.5.1验证上次的不足之处
1)10 人抢 0.11 元的包:
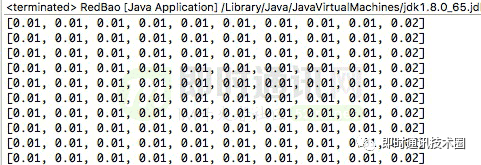
2)2 人抢 0.03 元的包:
3)6 人抢 0.09 的包:

5.5.2修改后的代码会不会对已知结论造成影响?
30 元的红包,10 人抢,操作 100 次。

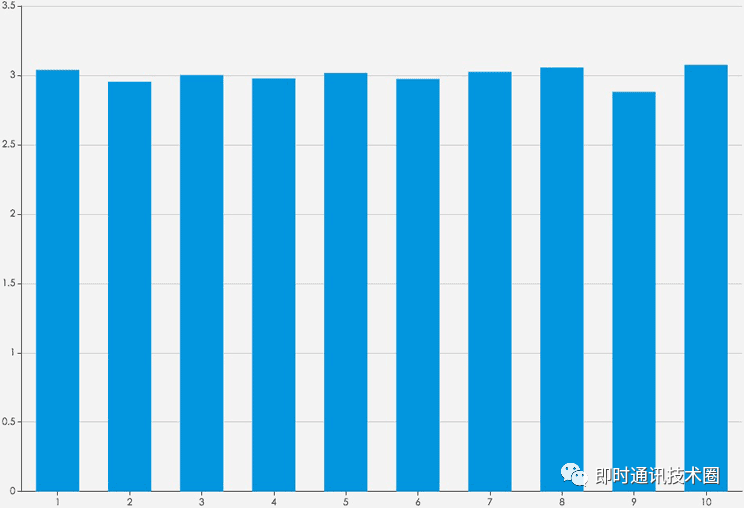
由上面两图可见,结论基本上没有改变。
5.6、结论
1)先抢后抢,金额期望都是相同的; 2)微信的红包算法很可能是预先分配给每人 0.01 的“底额”; 3)后抢者风险高,收益大。
5.7、补充
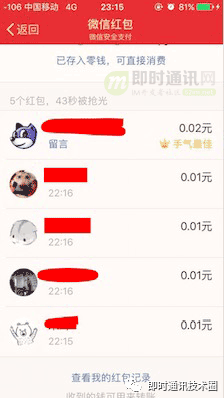
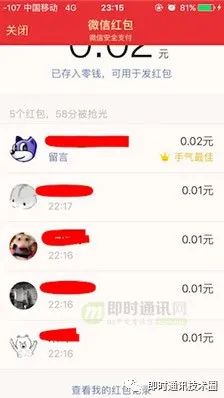
大家也可以试试。
以上,大概可以证明,微信红包是在分配前先给每个人 0.01 的最低金额的!
6、参考资料
[2] 微信红包算法的分析
[3] 微信红包的架构设计简介
[4] 微信红包的随机算法是怎样实现的?
另外,知乎上对于微信红包算法的讨论问题很多人参与,有兴趣可以上去看看,或许会有更多启发:《微信红包的随机算法是怎样实现的?》。
——————END——————
欢迎关注“Java引导者”,我们分享最有价值的Java的干货文章,助力您成为有思想的Java开发工程师!
赞+在看,小生感恩❤️
评论
