换个角度看世界!用代码了解数学符号
作者丨读芯术 来源丨读芯术（AI_Discovery）
学好数理化，走遍天下都不怕！这句话我们从小就听，放到今天似乎依然行得通。达芬奇说：“数学是一切科学的基础”，数学与代码之间也有着千丝万缕的联系。
似乎任何热衷于机器学习、数据科学的人都相信，总有一天，他们将研究透彻python库，畅享里面的数学知识。大量论文集将展现在你面前，详细说明其原理。对核心数学的理解越深入，你就越可能获得灵感，创造新方法。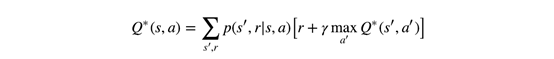
对于多年来钻研数学或从事机器数学学习的人来说，将上面这个方程式详细地解析为含义和代码并不难。但是对大部分普通人来说，无异于看天书。古代数学家似乎都喜欢用有趣的外观符号来表述直观的方法，但却使方程和变量复杂化了。
实际上，代码不仅可以编写程序，还可以让这些复杂的语言再次变得直观起来。加深对数学理解的最好方法就是编写代码段来描述方程式，这会让理解变得简单起来。
图源：unsplash
看过下面这些例子，相信你也会有这样的感觉。
求和与乘积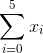
求和符号是迭代数学中最有用和最常用的符号之一。尽管设计复杂，但运算是相当简单且有用。
x = [1,2, 3, 4, 5]result = 0for i in range(5):result += x[i]Output of print(result)-> 15
如上所示，此符号代表从顶部的数字开始的for循环，顶端数字为最大值。在底部设置的变量将成为索引变量，并且每个循环的所有结果都将添加到总值中。
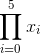
上面这个符号被称为乘积运算符，跟求和符号运算方式相似，但不会相加每个结果，而是将它们相乘。
x = [1,2, 3, 4, 5]result = 1for i in range(5):result *= x[i]Output of print(result)-> 120
条件括号
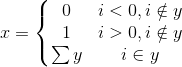
条件括号用于在特定条件下转换方程的等式。对于码农，常见的“ if”语句就是这样。把它用代码表述是这样的：
i = 3y = [-2, 3, 4, 1]result = 0if i in y:result = sum(y)elif i > 0:result = 1else:result = 0print(result) -> 6
如上所示，每一行括号中的正确表示法指定了每条路径应执行的操作。我也将多余的“包含”符号添加到每个条件中，以加强理解。我们检查了i值是否在y列表中。确认过后，返回数组的总和。如果i值不在数组中，将基于该值返回0或1。
阶乘
阶乘用“！”表示，几乎所有计算器上都有此符号。这个符号会好理解一些，不过代码会带你进一步了解它的原理。
5！将表示为：
result =1for i in range(1,5):result *= iOutput of print(result) -> 120
逐点操作和笛卡尔矩阵乘法再来看一下数据科学家们经常使用的语言库（矩阵乘法）如何完成操作。逐点操作很容易理解，简写为：
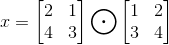
请注意，该操作首先要求每个矩阵必须具有这样的模型（即＃行 =＆＃列=）其代码如下所示：
y =[[2,1],[4,3]]z = [[1,2],[3,4]]x = [[0,0],[0,0]]for i in range(len(y)):for j in range(len(y[0])):x[i][j] = y[i][j] *z[i][j]print(x) -> [[2, 2], [12, 12]]
最后，让我们看一下机器学习中最常用的典型矩阵乘法。用复杂的术语来说，此运算为每个主要行与每个次要列的点积。
具体操作是：假设[#行，#列]→矩阵ixj要求#列（i）== #行（j）→最终输出的模型为[#行（i）， #列（j）]
看起来似乎很难理解，图片能帮助你直观了解这些操作。
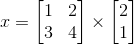
该方程的代码如下（使用numpy点法）：
y =[[1,2],[3,4]]z = [[2], [1]]# x has shape [2, 1]x = [[0], [0]]for i in range(len(y))for j in range(len(z):x[i][j] = np.dot(y[i], z[:, j])print(x) -> [[4],[10]]
图源：unsplash看完这几个简单的示例，是不是有种拨开迷雾见光明的感觉！
用简单的代码学习数学，你会大有收获的。
近期精彩内容推荐：
在看点这里
好文分享给更多人↓↓
评论