LWN：Julia 中的并发处理！

关注了就能看到更多这么棒的文章哦～

Concurrency in Julia

November 9, 2021

This article was contributed by Lee Phillips
DeepL assisted translation
https://lwn.net/Articles/875367/

Julia 编程语言起源于高性能科学计算领域，所以它自然会很好地支持拥有并发处理（concurrent processing）。不过，这些功能在 Julia 社区之外并没有多少人知道，所以很值得介绍一下该语言所支持的不同类型的并行（parallel）和并发（concurrent）计算。此外，即将发布的 Julia 1.7 版本为该语言的并发计算功能又带来了一块补充，也就是 "任务迁移（task migration）"。

Multithreading

Julia 支持各种形式的并发计算。多线程计算（a multithreaded computation）就是一种在不同的处理单元上同时进行工作的一种并发计算。多线程以及与此相关的术语并行计算（parallel computation），通常意味着各个线程都可以访问相同的主内存区域（main memory），因此它会用到同一台计算机上的多个 CPU core 或处理单元。

Julia 启动时如果没有带 -t 标志，那么就只会使用一个线程。要想让它利用所有可用的硬件线程（hardware thread），就可以使用 -t auto 这个参数。这会让它利用机器上所有的逻辑线程（logic threads）。不过这通常不是最好的选择，还是应该尽量用 -t n，其中 n 是物理 CPU core 的数量。例如，流行的英特尔酷睿处理器为每个物理核心提供了两个逻辑核心，使用了一种叫做超线程（hyperthreading）的技术实现倍增效果，在不同类型的计算中，这个特性可能有的会导致一些性能提升，有的则会降低一些性能。

为了演示 Julia 的多线程，我们将使用下面的函数，来检测一个数字是否为素数（prime）。本文中的例子代码都去掉了一些可能的优化方式，为了简化代码便于理解，isprime() 函数就是采用这个原则写出的：

function isprime(x::Int)
    if x < 2
        return false
    end
    u = isqrt(x) # integer square root
    for n in 2:u
        if x % n == 0
            return false
        end
    end
    return true
end

function isprime(x::Any)
    return "Integers only, please"
end

这个函数应该只检查整数（Int 是 Int64 的别名），所以我们利用了多重派发（multi dispatch）来创建了两个函数（method）：一个用来检查是不是素数，另一个函数则是用来在收到不是整数的数据的时候给出错误信息。每次都会根据最合适的类型来选择调用哪个函数，因此我们就可以不用在函数内部显式地写出类型检测代码，就可以把不正确的数据类型预先处理掉。

在我的测试中有一个很好用的多线程软件包，名为 Folds。这不是标准库中的软件包，所以你必须使用 Julia 的软件包管理工具先安装好。Folds 包提供了若干用于并发处理的 high-level 的宏和函数。它的名字意思是 "折叠"，也就意味着是用来简化数组的（reduction over an array）。Folds 提供了 map()、sum()、maximum()、minimum()、reduce()、collect() 等函数的多线程版本实现，以及其他一些对 collection （集合）的自动并行处理的支持。

这里我们使用 map() 来检查一系列数字是否为素数。如果 f() 是带有一个变量的函数，而 A 是一个数组，那么表达式 map(f, A) 就会对 A 的每个元素分别调用 f()，然后返回一个与 A 的个数相同的数组。用多线程操作来替换 map() 就是下面这么简单：

julia> @btime map(isprime, 1000:9999999);
  8.631 s (2 allocations: 9.54 MiB)

julia> @btime Folds.map(isprime, 1000:9999999);
  5.406 s (45 allocations: 29.48 MiB)

在 Julia 中，a:n:b 这种写法就定义了一个名为 "range" 的迭代器（iterator），它会从 a 到 b 按 n（默认为 1）这个步长来递增。在调用 map() 的时候，这些 range 就会被当作一个 vector。

Folds.map() 将数组分成相同长短的多个段（segments），给每个线程都分配一个 segment，并在每个 segment 上并行执行 map()操作。与本文中的所有实验一样，耗时统计都是使用 Julia 1.7rc1 版本来进行的。在这个测试中，我启动 REPL 的命令是 julia -t2。

BenchmarkTools 软件包中提供的 @btime 宏，会对后面的任务执行数次，然后报告出平均运行时间。时间显示，在我的双核机器上，运行速度与理想值也就是 2 倍来说相差不大，但代价是消耗了更多的内存。CPU 使用率的分析也证实了在第一次计算时只有一个 CPU core 在工作，而第二次计算时就有两个 core 来忙于处理了。

多线程处理的另一种方式是使用图形处理单元（GPU，graphics processing units）。GPU 最初是为了加速 3D 游戏和其他重度图形应用中都带有的那些并行图形计算（parallel graphics calculations）而设计的，它拥有数百或数千个浮点处理器，这些现在都可以作为阵列协处理器（array coprocessors）来用在各种应用中。GPU 计算的最佳对象就是那些算术操作和内存操作比例占比很高的并行计算。有一个名为 JuliaGPU 的组织，就提供了许多实现或依赖这种并行处理方式的 Julia 软件包。

map 操作本质上就是并行进行的，它会把某个函数独立地作用于集合中的每个元素，既不会从其他元素中读取，也不会向其他元素进行写入。正因为如此，传统的 map 可以替换成多线程版本的实现，不会改变程序中的其他内容。也不会出现那些同时访问同一数据这类复杂问题。

而现实生活中的程序都会包含一些容易并行化的部分，也同时包含一些需要小心处理的部分，还有一些完全不能并行化的部分。比如来讨论一下简单的星系模拟的工作，多个星体在相互引力的影响下运动。每个物体上受到的力都必须要先检查所有其他物体的位置来计算得出（超出一定距离可以忽略，具体取决于最终的精度要求）。尽管这部分计算可以并行化，但这就比上面讨论的 map() 操作更加复杂了。但是在将来自各个位置的受力存储下来之后，每个物体的速度变化就可以独立于其他物体来计算出来了，这可以利用一个简单的 map() 结构来很容易进行并行化计算。

Julia 就具有所有那些用在更复杂的场景下的并发计算的支持。使用 @threads 宏就可以使一个 for 循环成为多线程的的实现：

  Threads.@threads for i = 1:N
        
  end

在这种情况下，假如我们有两个线程，其中一个线程会从 1 到 N/2 来进行循环，另一个线程是从 N/2 到 N 进行循环。只要有多个线程需要访问到同一个数据，那么这些数据就必须用锁来保护起来，这个功能是由 lock()函数来提供的。Julia 也支持使用 Atomic 数据类型来防止一些 race condition （竞态问题）。程序不可以简单地修改这种类型的数据，除非是使用比如 Threads.atomic_add!()和 Threads.atomic_sub!() 这样的原子操作来代替正常的加法和减法。

Distributed processing

另一种类型的并发则牵涉到多个配合起来的异步任务 coroutines，Julia 称之为 Tasks。这些程序可以共享同一个线程、或者分发给多个线程、被分发到集群中的不同节点上、甚至分发到互联网上位于不同位置的分布式系统上。所有这些形式的分布式计算（distributed computing）都有一个共同的特点：处理器不可以直接访问到相同的内存位置，所以数据必须要被传送到需要对其进行计算的地方。

tasks 很适合这样的场景：程序需要耗费一些时间来启动一个工作，但这个程序可以继续执行，因为它并不需要立即得到那个工作的计算结果。例如从互联网上下载数据、复制文件、或者执行一个长期运行的计算而之后才需要其计算结果。

当用 -p n 标志调用 Julia 时，除了主执行进程外，还会初始化出 n 个工作进程（executive process）。这两个多进程标志（multiprocessing flags）可以结合起来使用，如 julia -p2 -t2。这就会启动两个工作进程，每个进程可以使用两个线程来进行计算。在本节的例子中，我使用 julia -p2。

"手动" 地启动一个 task，就是使用 @spawnat :any expr 这个宏调用方式。其指定了一个 task 来计算 expr 这个表达式，会使用系统所选择的那个工作进程来计算。工作进程是从 1 开始的整数标识符，在 :any 这个位置使用一个整数来代替的话，就会让 task 在该特定进程中孵化运行。

常见做法是使用 pmap() 这个分布式版本的 map() 操作，其会由 -p 参数来 import 进来，也会进行相同的计算工作，但是首先会将数组分解成若干部分，向每个工作进程发送相同大小的一部分，由其来并行执行 map 操作，然后收集和汇总结果。举个例子，下面是使用著名的收敛非常缓慢的莱布尼兹和方式来估算 π（见下图）。

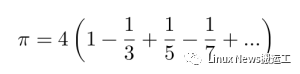
[莱布尼兹求和方程]

函数 leibniz(first, last, nterms) 会返回一个数组，其中包含前两个参数之间的每一个 nterms 项的结果：

@everywhere function leibniz(first, last, nterms)
    r = [] 
    for i in first:nterms:last # Step from first to last by nterms
        i1 = i
        i2 = i+nterms-1
        # Append the next partial sum to r:
        push!(r, (i1, i2, 4*sum((-1)^(n+1) * 1/(2n-1) for n in i1:i2)))
    end  
    return r  
end

@everywhere 宏也是由-p 标志 import 进来的，它会将函数和变量的定义广播给所有的工作进程。这是一个必要工作，因为工作进程与主进程并没有共享内存。leibniz()函数是 Leibniz sum 的简单翻译出来的版本，其会用 sum() 函数将生成器表达式（generator expression）中的项加起来。在每一组 nterms 项之后，会将累积的部分结果放入 r 数组，完成后将此数组返回回去。

为了测试 pmap()的性能，我们可以用它来同时计算前 2×108 项：

julia> @btime r = pmap(n -> leibniz(n, n+10^8-1, 1000), [1, 10^8+1]);
  7.127 s (1600234 allocations: 42.21 MiB)

使用普通 map 的版本，只用了一个进程，就需要几乎两倍的时间（但只使用了 23%的内存）。

julia> @btime r = map(n -> leibniz(n, n+10^8-1, 1000), [1, 10^8+1]);
  13.630 s (200024 allocations: 9.76 MiB)

下图是对莱布尼兹数列的前 2×108 项求和的结果。

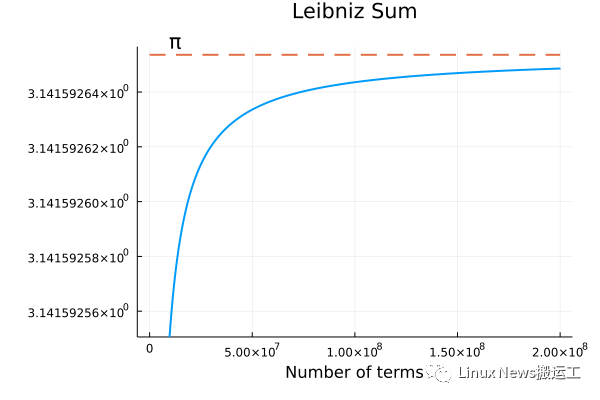
[莱布尼兹求和收敛]

这个分布式处理的版本比起普通 map() 操作消耗了多得多的内存空间，这也是我在大多数场合都观察到的情况。pmap() 看起来最适合那些粗粒度的多任务处理（coarse-grained multiprocessing），它是一种对小范围的输入集合（a small collection of inputs）的耗时操作有效进行加速的处理方法。

Julia 的分布式处理机制也可以跨越多个机器。当给定了一个文件中含有各个互联网 IP 地址时，Julia 就会使用 SSH 和公钥认证来经过互联网生成 job，这样就可以让本地开发出来的分布式代码在配置好的计算机网络上运行了，只需进行少量修改就好。

Tasks and task migration

Julia 支持的另一种并发处理可以被称为 asynchronous multithreading （异步多线程）。它会使用 Julia tasks 来进行计算，但会分配给一个进程中的多个线程去执行。因此所有的任务都可以访问到相同的内存区域，合作来进行多任务处理。在本节的例子中，我用 julia -t2 启动了 Julia，所以我的两个 CPU 核上各有一个线程。

我们可以通过一个宏来启动一个任务并将其自动安排在一个可用的线程上：a = Threads.@spawn expr。这将返回一个 Task 对象。我们调用 fetch(a) 就可以等待该 Task 完成并获取 expr 的返回值。

对于一组运行时间大致相等的 Task 的计算，基本可以看到执行速度会与 CPU 线程的数量有接近线性的关系。在过去的 Julia 版本中，一旦某个任务被安排在一个线程上了，就会被卡在那里直到最终完成。这样如果某些任务比其他任务需要更长的时间，那么就可能会产生调度问题，导致那些承载了任务较少的 Task 的线程可能就会变得很空闲，而任务较重的那些 Task 则继续在它们原来的线程上争夺 CPU 时间。在这种涉及到运行时间非常不平等的多个 Task 的情况下，我们可能就看不到速度提升的线性关系了，因为有资源被浪费了。

在 Julia 1.7 版本中，task 允许在线程之间迁移了。因此可以被重新安排到可用的线程上，而不是停留在它们最初被分配的线程。这项功能目前还缺乏文档，但我使用 Threads.@spawn 启动的那些 task 可以在调用 yield() 时被迁移，yield() 函数的用途是暂停一个 task 并允许另一个被调度到的 task 运行。

为了能直接观察到线程迁移的效果，我就需要能够打开和关闭这个功能。我们可以编译一个没有启用该功能的 Julia 版本来进行测试，但其实还有一个更简单的方法。ThreadPools 包提供了一组用于并发处理的宏。我在实验中使用了 @tspawnat 宏，用其产生的 task 都可以迁移，就像使用 Threads.@spawn 产生的任务一样，但是使用@tspawnat 也允许我可以简单地修改来产生一个不允许迁移的 task。

Monte Carlo 物理模拟，或者概率建模（probabilistic modeling）都是异步多线程计算的理想场景。可以先运行一组模拟（simulation），这些 simulation 中除了控制每个任务计算细节的一系列伪随机数之外，其他都是完全一样的。所有的任务都是相互独立的，当它们都完成之后就可以得到各种平均数及其数据的分布情况。

我在实验中写了一个简单的程序来考察 Julia 的伪随机数生成函数 rand() 的统计特性，调用该函数会返回一个在 0 到 1 之间的均匀分布的随机数，而不需要任何参数。下面的函数每次调用时指定参数 n，就会进行 n 次生成一个随机数的操作，并把数据分成 n/10 组，报告出每组数字的平均值：

function darts(n)
      if n % 10 != 0 || n <= 0
          return nothing
      end
    a = Threads.threadid()
    means = zeros(10)
    for cyc in 1:10
        yield()
        s = 0
        for i in 1:Int(n/10)
            s += rand()
        end
        means[cyc] = s/(n/10)
    end
    return (a, Threads.threadid(), time() - t0, n, means)
end

该程序的参数 n 必须是 10 的倍数。它还有几行代码用来记录它是在哪个线程上运行的，以及完成时间。这个完成时间是从一个全局性的 t0 时刻开始计算的。在这 10 组数据的每一组这个周期开始之前，它都会先调用 yield()，使得调度器可以切换到线程上的另一个 task 去，并且在线程迁移时也会将 task 转移到另一个线程上。

举个例子，如果我们运行 darts(1000)，我们会得到 10 个均值，每个均值都是 100 个随机数的计算结果。根据中心极限定理（central limit theorem），这些平均值应该符合正态分布（normal distribution），其平均值与 underlying （uniform）distribution 的平均值相同。

为了得到样本并绘制其分布情况，我启动了 20 个 task，每个 task 都运行了 n=107 的 darts() 程序。这样就运行了 200 个随机试验（trial），每个试验（trial）中都选取了 100 万个随机数，然后计算并记录其平均值。我们还需要对分布的平均数有一个高度准确的估计，所以我又启动了一个 n=109 的任务来对此进行计算。我们知道理论上的平均数应该是 0.5，所以这个结果会告诉我们 rand() 的偏差有多大。通过一个简单的修改，该程序可以用于其他基础分布（underlying distribution），不过那些分布的平均值我们可能就无法这么简单地分析得知了。

我用下面的方法启动了这些 tasks：

begin
    t0 = time()
    tsm = [@tspawnat rand(1:2) darts(n) for n in [repeat([1e7], 20); 1e9]]
end

每个 task 都可以拿到 t0，所以他们都可以报告出他们完成耗时多少。最开始调用的 rand(1:2) 会将每个 task 以相等概率分配给第一个线程或第二个线程。我重复五次进行了这个实验，然后跑另一个实验也执行了五次，另一个实验中除了使用了我修改过的 @tspawnat 宏来禁用线程迁移之外，其他没有什么变化。

为了查看每个一个实验的分布情况，我们可以将样本平均值收集到一个数组中，然后用 Plots 包中的 histogram()函数来绘制出来。Julia 绘图系统有个概述文章介绍了如何使用 histogram() 以及本文中使用到的其他绘图函数。结果显示在下图中，这个叠加上来的条形图就是使用 109 数字计算的平均值。

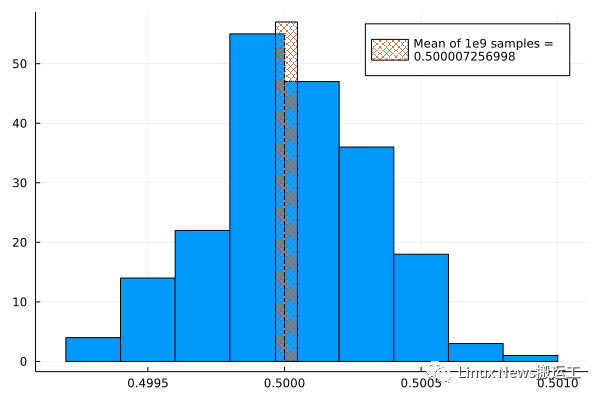
[随机数分布]

该分布近似于正态分布，均值也正确。

实验包括了 20 个耗时较短的 task 以及一个需要 100 倍时间的 task。我乐观地认为这可以展示出线程迁移的效果，因为调度器就可以有机会把 task 从那个包含了长期运行的计算的线程上移走，这正是线程迁移功能所希望改善的情况。至于那些各个 task 的计算资源需求很接近的计算场景则应该不会从迁移中得到什么好处。

在五次实验中，启用了线程迁移的 21 个任务的完成时间平均值为 0.71 秒，而禁用了迁移的测试中耗时平均值为 1.5 秒。仔细深入查看这些耗时数据就可以了解到线程迁移是如何使 job 完成的速度提高了一倍。下图显示了所有 10 个实验的完结时间（return time），并画了一条线来帮助人们可以看出最快的那个实验的耗时数据。

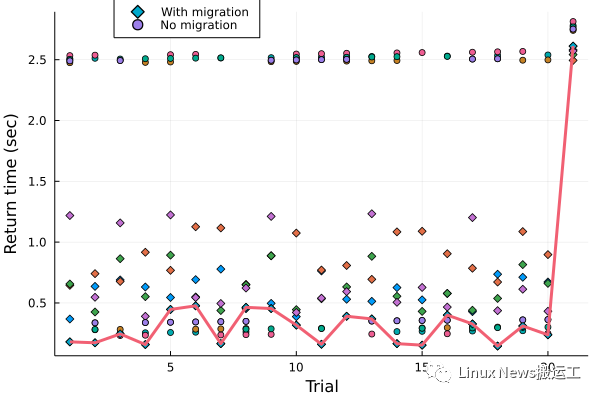
[任务迁移图]

数据显示，运行 darts(1e7) 需要 0.024 秒，darts(1e9) 需要 2.4 秒，这个数据符合我们期望的运行时间比例。编号为 21 的试验就是 darts(1e9) 的这个任务，它在并行运行时需要大约 2.5 秒。该图清楚地表明，在没有迁移的情况下大约有一半的 task 会被卡住，与那一个最繁重的 task 任务共用同一个线程。另一半任务则会很快完成，在此之后，这个线程就会无事可做，被浪费了。对比情况下，线程迁移则会将 task 转移到空闲线程上，从而得到更好的负载平衡，也就可以更快地完成整个工作。观察 Threads.threadid() 调用的返回值，也证实了大约一半的任务会进行迁移。

这个实验表明，新的线程迁移功能正在如预期的那样起到了效果。在任务的运行时间明显不平衡，或者有一些任务被阻塞在等待 I/O 或其他 event 的情况下，线程迁移功能可以加快异步多线程计算的速度。

在本节和上一节这种类似的计算任务中，任务之间是完全独立执行的，不需要协调。如果一个程序中有些地方必须要等待所有异步任务完成后才能进入下一阶段，那这里就可以使用 @sync 宏了，就会一直等到在宏出现的范围内所产生的 task 都完成。

Conclusion

并发（concurrency），本质上就是一件很困难的的事情。并发程序（concurrent program）更加难调试和理解。Julia 并没有消除这些困难，也就是说程序员仍然需要自己注意 race condition、一致性（consistency）和正确性（correctness）。但是 Julia 的宏以及那些用于 task 与数据并行处理的函数在许多情况下可以让简单的事情变得更容易，而更复杂的问题也可以变得可以实现出来了。

这个领域的开发也非常活跃，从 Folds 等软件包，到比如调度器操作的实现细节（这是近期实现的任务迁移功能的底层功臣）。我们可以期待 Julia 的并发计算的情况将会继续提高。也同样需要认识到，并发生态系统的一些更好的功能仍然未能加入标准库和官方文档，想要利用好这些产品的优势的程序员都需要努力跟上这个不断变化的世界。

全文完
LWN 文章遵循 CC BY-SA 4.0 许可协议。

长按下面二维码关注，关注 LWN 深度文章以及开源社区的各种新近言论～