肝了好多天-动态规划十连-超细腻解析
No.1
最简单的动态规划题目
侄女5岁现在开始学习加减法了,每次做数学都离不开她的小手指,超过5的就开始数另一个手的手指,真是汗颜啊
有一天,我问她
“1+1+1+1+1等于多少?”
“搬起小拇指,就开始数了,5!”
“那么再加一个1呢?”
“当然是6了” -脱口而出
“这次你怎么算这么快的?”
“刚刚不是5吗,加1就是6了啊”
“所以你不需要重新计算,因为你记得之前的答案是5!动态规划就是说:记住之前的东西可以节省时间”
玩归玩,闹归闹,别拿dp开玩笑!
来瞅一眼科普中国科学百科的词条解释
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。
看不完的童鞋跳过,咱整点简单点的
其实刚刚这道题应该算是最简单的动态规划题目了。
我们可以看出这道题有什么特点呢?
我们知道之所以最后一步加1会计算的那么快,大部分要归功于之前计算过答案是5,如果我们把问题归纳为一个子问题,我想要计算每一步的答案,就可以列出一个方程:f(x) = f(x -1) + 1, 大家别对f(x)发怵,就把它当做一个简单的方法。
其中,f(x)为第几步的值,设定一个初始值,x > 0, 则第一步
f(1) = 1;
f(2) = f(1) + 1;
...
f(6) = f(5) + 1
在程序的世界里,用什么东东来存一个可以记录之前结果值的数据结构呢?
显而易见:数组呗。直接利用下标来存,巴适, 这就是动态规划里的动态,规划就是限定一些边界和初始化。
看到这里,老铁,你就会动态规划了,来看第二题。
No.2
leecode 322: 你有三种硬币,2元、5元、7元,每种硬币足够多,买一本书需要27元,用最少的硬币组合

怎么感觉像是回到了小学应用题?
--简单分析一下:最小硬币组合 -> 尽量用大的硬币
这傻不拉几的题谁出的,这么简单
7+7+7=21,21+2+2+2=27, 6枚硬币
卧槽
7+5+5+5+5=27, 5枚硬币
我们可以很暴力的想一想,从大往小的算,可以加起来不超过27,比如
7+7+7+7 > 27 (排除)
7+7+7+5 或者 7 +7 +7+2+2+2 6枚
....
穷举太慢了,还会涉及到很多的重复计算,如果我想要27以内的任何值最小的硬币组合呢,想想都头大了吧。
既然计算机可以通过内存保存之前的内容,又快,很明显,我们开一个数组来保存之前的状态。
重点预警
1.1. 动态规划组成部分1:确定状态
简单的说,解动态规划的时候需要开一个数组,数组的每个元素f[i]或者f[i][j]代表什么,类似数学题中x, y, z代表什么
解动态规划需要两个意识:
最后一步
子问题
最后一步
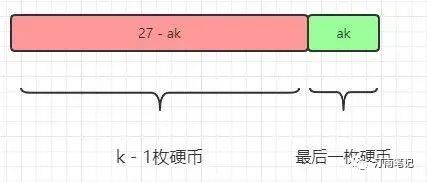
刚刚第一题不是说了嘛,最后一步的计算结果是5。对于这道题,虽然我们不知道最优策略是什么,但是最优策略肯定是K枚硬币,a1, a2, ....ak面值加起来是27
所以一定有一枚最后的硬币:ak.
除掉这么硬币,前面硬币的面值加起来是27-ak
关键点1:
我们不关心前面的k-1枚硬币是怎么拼出27-ak的(可能有一种拼法,也可能有100种拼法),而且我们现在甚至还不知道ak和K, 但是我们确定前面的硬币拼出了27-ak
关键点2:
因为是最优策略, 所以拼出27-ak的硬币数一定要最少,否则这就不是最优策略了
子问题
所以我们就要求:最少用多少枚硬币可以拼出27-ak
原问题是最少用多少枚硬币拼出27
我们将原问题转化了一个子问题,而且规模更小:27-ak
为了简化定义, 我们设状态f(x)=最少用多少枚硬币拼出x
等等,我们还不知道最后的那枚硬币ak是多少
很明显,最后的那枚硬币只能是2,5或者7
如果ak是2, f(27)应该是f(27-2)+1(1代表最后一枚硬币2)
如果ak是5, f(27)应该是f(27-5)+1(1代表最后一枚硬币5)
如果ak是7, f(27)应该是f(27-7)+1(1代表最后一枚硬币7)
所以使用最少的硬币数=f(27) = min{f(27-2)+1, f(27-5)+1, f(27-7)+1}
1.2. 动态规划组成部分2:转移方程
设状态f(x)=最少用多少枚硬币拼出x
对于任意的x : f(X) = min{f(X-2)+1, f(X-5)+1, f(X-7)+1}
1.3. 动态规划组成部分2:初始条件和边界情况
提出问题
x-2, x-5, x-7 小于0怎么办?
什么时候停下来?
1.3.1
如果不能拼出Y, 就定义f[Y] = 正无穷
例如f[-1], f[-2] = 正无穷
例如:拼不出f[1]=min{f(-1)+1, f(-3)+1, f(-6)+1}
初始条件:f[0] = 0
2.4. 动态规划组成部分2:计算顺序
计算:f[1], f[2], ... f[27]
当我们计算到f[x], f[x-2], f[x-5], f[x-7] 都已经得到结果了
如图:

上图7只需要一个硬币。
f[x] = 最少用多少枚硬币拼出x
f[x] = ∞ 表示无法用硬币拼出x
参考代码
public static int coinChange(int [] A, int M ) {
int[] f = new int[M+1];
int n = A.length;
f[0] = 0;
int i,j;
for (i = 1; i<=M; i++) {
f[i] = Integer.MAX_VALUE;
for (j = 0; j< n;j++) {
// 边界条件判断
if (i >= A[j] && f[i - A[j]] != Integer.MAX_VALUE) {
f[i] = Math.min(f[i - A[j]] + 1, f[i]);
// System.out.println(i + "=" +f[i]);
}
}
}
if (f[M] == Integer.MAX_VALUE) {
f[M] = -1 ;
}
return f[M];
}
@Test
public void isCoinChange() {
int xx = {1,2,3};
int b = 6;
int i = coinChange(xx, b);
Assert.assertNotNull(i);
}
😄
No.3
leecode 62 :不同路径
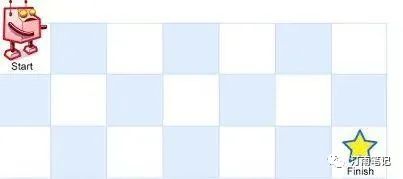
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
看了上面的解题步骤,按部就班的来
2.1. 动态规划组成部分1:确定状态
最后一步
无论机器人用何种方式到达右下角,总有最后挪动的一步:-向右或者向下
如果所示,我们设右下角的坐标为(m-1,n-1)
那么最后一步的前一步机器人的位置在(m-2,n-1)或者(m-1,n-2)
子问题
那么,如果机器人有x种方式从左上角走到(m-2,n-1), 有Y种方式从左上角走到(m-1,n-2), 则机器人有X+Y的方式走到(m-1,n-1)
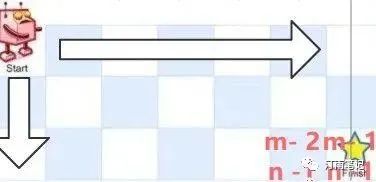
问题转化为,机器人有多少种 方式从左上角走到(m-2,n-1)或者(m-1,m-2)
如果走到是(m-2,n-1)如图:

我们可以直接干掉最后一列
同理如果是走到(m-1,n-2)行就减少一行。
状态:
设f[i][j]为机器人有多少种方式从左上角走到(i,j)
2.2. 动态规划组成部分2:转移方程
对于任意一个格子:
f[i][j] = f[i-1][j] + f[i][j-1]
1 2 3
1代表机器人有多少种方式走到[i][j]
2代表机器人有多少种方式走到f[i-1][j]
3代表机器人有多少种方式走到f[i][j-1]
2.3. 动态规划组成部分3:初始条件和边界情况
初始条件:f[0][0]=1,因为机器人只有一个方式到左上角
边界情况:i=0或j=0,则前一步只能有一个方向过来,也就是说第0行或者第0列,每走一步只有一种情况,则f[i][j] = 1,其他区域都满足转移方程。
3.4. 动态规划组成部分4:计算顺序
按行计算,为什么按行计算呢?
对于这道题来说,按行计算在计算到f[1][1]时,f[0][1]和f[1][0]都已经计算了,同样按列计算这两坐标也计算了,不用再次计算。
f[0][0] = 1
计算第0行:f[0][0],f[0][1],...,f[0][n-1]
计算第1行:f[1][0],f[1][1],...,f[1][n-1]
...
计算第m-1行:f[m-1][0],f[m-1][1],...,f[m-1][n-1]
时间复杂度:O(mn)
参考代码
public int uniquePaths(int m, int n) {
int[][] f = new int[m][n];
int i,j;
for (i = 0; i<m; i++) {
for (j = 0; j< n; j++) {
if (i == 0 || j == 0) {
f[i][j] = 1;
} else {
f[i][j] = f[i -1][j] + f[i][j-1];
}
}
}
return f[m-1][n-1];
}
@Test
public void isUniquePaths() {
int i = uniquePaths(3, 3);
Assert.assertNotNull(i);
}
能看到这里的朋友,你已经超过80%的人,可能现在你的脑袋开始有点晕了,刷题就是这样,刷几道就会头疼,休息下就好了,这玩儿意儿看得就是坚持.
总结一下
什么题可以选择动态规划来做?
1.计数
有多少种方式走到右下角
有多少种方法选出k个数是的和是sum
2.求最大值最小值
从左上角走到右下角路径的最大数字和
最长上升子序列长度
3.求存在性
取石子游戏,先手是否必胜
能不能选出k个数使得和是sum
好叻!接下来咱们整第四道题。
No.4
leecode 5. 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:输入: "babad"
输出: "bab" 注意: "aba" 也是一个有效答案。
示例 2:输入: "cbbd"
输出: "bb"
看了之前的文章,我们就四步走吧
1.1. 动态规划组成部分1:确定状态
简单的说,解动态规划的时候需要开一个数组,数组的每个元素f[i]或者f[i][j]代表什么,类似数学题中x, y, z代表什么
在这道题中,我们定义f[i][j] 表示字符串 s 的第 i 到 j 个字母组成的串是否为回文串
解动态规划需要两个意识:
最后一步
子问题
最后一步
我们用示例一来讲解,下图是第一步和第二步的判断过程,很明显最后一步为下标为4的字母b与前面所有元素进行比较,得出最长的回文子串。

子问题
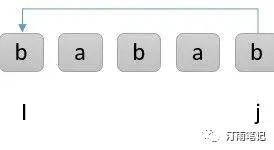
我们可以看到如果f[i] =f[j],要判定它是一个回文串,需要判定
f[i]j] = f[i+1]f[j-1] :从i到j是一个回文串,那么从i+1到j-1一定也是一个回文串
也就是如上图需要判定a=a
1.2. 动态规划组成部分2:转移方程
对于从i到j长度的字符串,判定它是一个回文串:
f[i]j] = f[i+1]f[j-1]
同时我们也知道,f[i+1][j-1]这是一个已知的,因为最后一步的上一步已经将结果保存,也就是f[i+1][j-1] = f[i+2]f[j-2]
1.3. 动态规划组成部分3:初始条件和边界情况
当剩余判定字母个数<3 并且 f[i] = f[j],它一定是回文串。
对于字母本身来说f[i][i],从i到i的字符串,它也是回文。
1.4. 动态规划组成部分4:计算顺序
如上图,我们用j去匹配0~i (i < j)
它的时间复杂度是On^2,由于是二维数据空间复杂度也是On^2
当然也有其他的解决办法如中心扩散和马拉车。
参考代码
// 动态规划
public String longestPalindrome(String s) {
// 特判
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i, j] 是否是回文串
boolean[][] dp = new boolean[len][len];
char[] charArray = s.toCharArray();
for (int i = 0; i < len; i++) {
dp[i][i] = true; // 对本身来说就是回文
}
for (int j = 1; j < len; j++) {
for (int i = 0; i < j; i++) {
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1]; // 要满足这个条件,必需先满足j - i > 3考虑边界
}
}
// 只要 dp[i][j] == true 成立,就表示子串 s[i..j] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
@Test
public void islongestPalindrome() {
String i = longestPalindrome("babaxaxab");
Assert.assertNotNull(i);
}
准备来一道非常实用的题目👍 👍 👍
No.5
leecode 10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aab" p = "c * a * b " (*号无空格)
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 2:
输入:s = "mississippi" p = "misisp*."
输出:false
解释:第二个*不能匹配si
2.1. 动态规划组成部分1:确定状态
wc,你倒是说说怎么确定要用动态规划来做啊?
看题目,需要逐步匹配
没有时间复杂度空间复杂度限制,你可以选择>On的
跟前面题很类似,这里需要考虑* 和 .的情况。
尝试根据步骤写出转移方程
在这道题中,我们定义f[i][j] 表示字符串 s 的前 i 个字符与 字符串p的前 j 个字符是否匹配
解动态规划需要两个意识:
最后一步
子问题
最后一步
我们用示例来讲解 :s = "aaab" p = "aa*b"
根据题目意思,我们知道s要被全匹配,我们直接用s去匹配p字符串的每一个字符,这样我们的最后一步就是用s字符串中的b字符去匹配p字符串的每一个字符,匹配最后一个字符为b是否相等。
子问题
有几种情况需要讨论,也就是用s去匹配p最后一个匹配的字符j
如果都是字符,只需要判断:f[i][j] = f[i-1][j-1]
如果是“.” ,说明可以匹配s的最后任意一个字符,也只需:
f[i][j] = f[i-1][j-1]
如果是“*”,分两种情况一种是匹配零个字符,一种是匹配1个或多个字符
如果是匹配零个字符:f[i][j] = f[i][j-2] ,因为如果j是*,我们就可以对p的j-1匹配任意次数,当然零次就是j-2了。
如果是匹配1个或多个字符:f[i][j] = f[i-1][j],匹配 s 末尾的一个字符,将该字符扔掉,而该组合还可以继续进行匹配,简单点说,零个我们判定了,如果是一个我们扔掉一个字符,如果能匹配则保存,如果匹配两个,我们是知道匹配s的上一个字符的结果的,直接匹配就行,同样匹配多个也是如此。(匹配多个是根据前一个的匹配结果得出来的)
2.2. 动态规划组成部分2:转移方程
在子问题中我们分析的几种情况就是转移方程
2.3. 动态规划组成部分3:初始条件和边界情况
因为要涉及到i-1和j-1,注意边界
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0]=true
2.4. 动态规划组成部分4:计算顺序
用s去匹配p字符串的每一个字符
它的时间复杂度是Onm,由于是二维数据空间复杂度是Onm
参考代码
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
f[i][j] = f[i][j - 2];
if (matches(s, p, i, j - 1)) {
f[i][j] = f[i][j] || f[i - 1][j];
}
} else {
if (matches(s, p, i, j)) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
public boolean matches(String s, String p, int i, int j) {
if (i == 0) {
return false;
}
if (p.charAt(j - 1) == '.') {
return true;
}
return s.charAt(i - 1) == p.charAt(j - 1);
}
@Test
public void isisMatch() {
boolean i = isMatch("aa", "a*");
Assert.assertNotNull(i);
}
No.6
继续干,继续干❤️❤️❤️❤️
leecode 32. 最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
提示:
0 <= s.length <= 3 * 104
s[i] 为 '(' 或 ')'
看了之前的文章,我们就四步走吧
1.1. 动态规划组成部分1:确定状态
简单的说,解动态规划的时候需要开一个数组,数组的每个元素f[i]或者f[i][j]代表什么,类似数学题中x, y, z代表什么
wc,你倒是说说怎么确定要用动态规划来做啊?
看题目,需要逐步验证最长长度
没有时间复杂度空间复杂度限制,你可以选择>=On的
跟前面题很类似,这里需要考虑生成括号的情况。
尝试根据步骤写出转移方程
在这道题中,我们定义d[i]表示以下标 ii字符结尾的最长有效括号的长度
解动态规划需要两个意识:
最后一步
子问题
最后一步
我们用下图来讲解,i作为最后一个括号判断,我们只对为左括号做判断,左括号分两种情况,具体看子问题拆分。 
子问题
第一种情况为:...()
因为括号前面可能还有有效的括号,之前我们定义了d[i] 表示下标i字符结尾的最长有效括号的长度,所以可以推导出:
d[i] = d[i-2] + 2
第二种情况为:...))
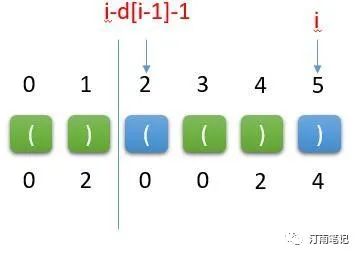
如图,下标为2:i - d[i-1] -1
提出一个疑问:在下标2和5之前可能存在多个有效括号,其实都是d[i-1],因为我们定义的:d[i-1] 表示下标i-1字符结尾的最长有效括号的长度
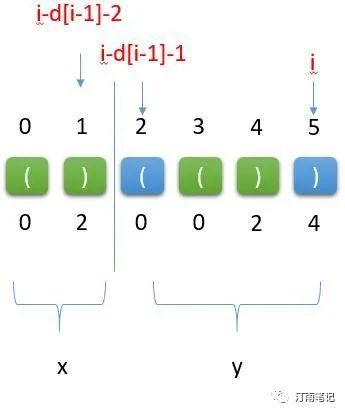
最长有效括号的长度 :
d[i] = x + y
这里x = d[i - d[i-1] -2]
这里y = d[i-1] + 2
因此 :d[i] = d[i - d[i-1] -2] + d[i-1] + 2
1.2. 动态规划组成部分2:转移方程
d[i] 表示下标i字符结尾的最长有效括号的长度
d[i] = d[i - d[i-1] -2] + d[i-1] + 2
1.3. 动态规划组成部分3:初始条件和边界情况
跟之前有些题一样,我们需要判断第i字符去判断第i-1个字符,所以i从1开始遍历,判断数组i-2需要考虑越界。
① ...() : i >=2
② ...)) : i - d[i-1] > 0 对应 :())
1.4. 动态规划组成部分4:计算顺序
从左往右
它的时间复杂度是On,空间复杂度也是On
当然也有其他的解决办法如栈
参考代码
public int longestValidParentheses(String s) {
int maxans = 0;
int[] dp = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]);
}
}
return maxans;
}
@Test
public void isLongestValidParentheses() {
String s = "()(())";
longestValidParentheses(s);
}
No.7
这道题相对于就简单一些啦---来自秃顶的工程师👥👥👥👥👥
leecode 42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
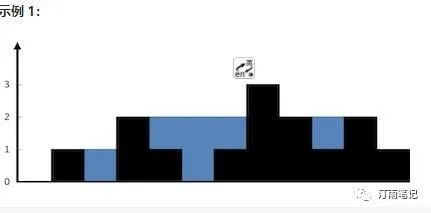
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
0 <= n <= 3 * 104
0 <= height[i] <= 105
看了之前的文章,我们就四步走吧
这道题相对而言,提升了难度,常规的题,我们的计算顺序一般是从左到右,或者从右到左,亦或是从上到下。
1.1. 动态规划组成部分1:确定状态
简单的说,解动态规划的时候需要开一个数组,数组的每个元素f[i]或者f[i][j]代表什么,类似数学题中x, y, z代表什么
wc,你倒是说说怎么确定要用动态规划来做啊?
看题目,需要逐步验证最长长度
没有时间复杂度空间复杂度限制,你可以选择>=On的
跟前面题很类似,这里需要考虑每一步最高的高度取低位高度,因为可能形成低洼
尝试根据步骤写出转移方程
在这道题中,我们定义d[i]表示以下标 i字符结尾的最多的有效雨水
解动态规划需要两个意识:
最后一步
子问题
最后一步
我们可以利用填满法来降低复杂度。去掉低洼的情况。
先从左到右来看,求出每个位置的最大高度(深度)
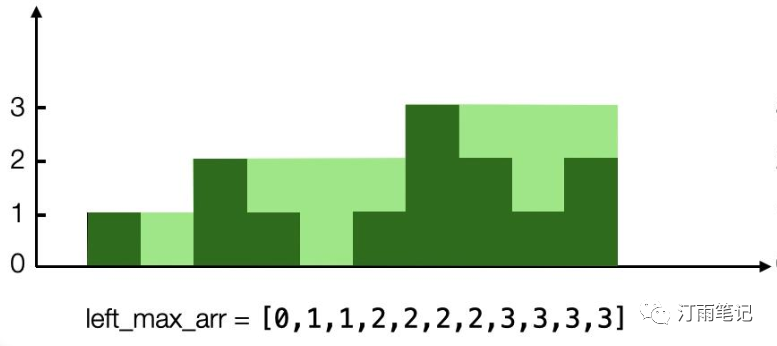
从右往左看,求出每个位置的最大高度
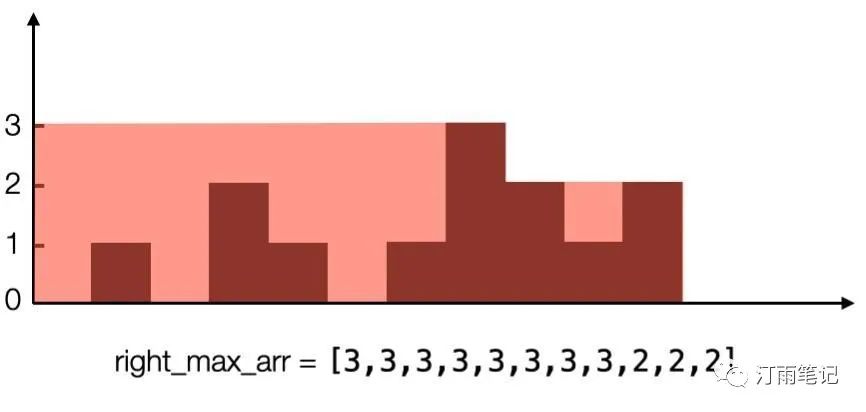
我们在来看它们重叠之后的效果
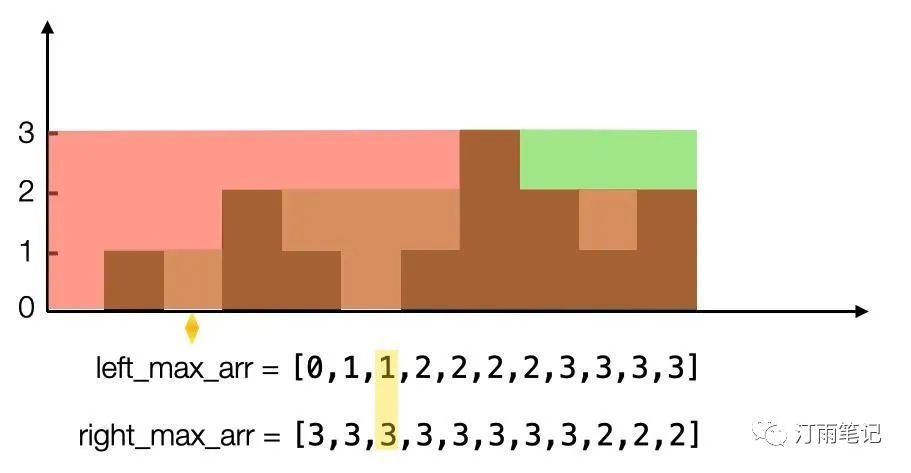
这样每个位置的最小值 - 高度就是每个位置的蓄水值。
子问题
我们存储了从左到右和从右到左每个位置的最大值
从重叠的图中可以看到最后一个位置的最小值为2,减去高度,蓄水值为0.
1.2. 动态规划组成部分2:转移方程
ans += Math.min(left_max[i], right_max[i]) - height[i];
1.3. 动态规划组成部分3:初始条件和边界情况
1.4. 动态规划组成部分4:计算顺序
从左到右 + 从右到左
它的时间复杂度是On,空间复杂度也是On
当然也有其他的解决办法如栈
参考代码
public int trap(int[] height) {
if (height == null || height.length == 0)
return 0;
int ans = 0;
int size = height.length;
int[] left_max = new int[size];
int[] right_max = new int[size];
left_max[0] = height[0];
for (int i = 1; i < size; i++) {
left_max[i] = Math.max(height[i], left_max[i - 1]);
}
right_max[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
right_max[i] = Math.max(height[i], right_max[i + 1]);
}
for (int i = 1; i < size - 1; i++) {
ans += Math.min(left_max[i], right_max[i]) - height[i];
}
return ans;
}
@Test
public void istrap() {
int[] candidates = {2, 0, 6, 1};
int i = trap(candidates);
Assert.assertNotNull(i);
}
No.8
这道题跟第五题很类似,如果看懂了第五题,那么这题肯定是信手拈来❤️❤️❤️❤️
leecode 44. 通配符匹配
给定一个字符串 (s) 和一个字符模式 (p) ,实现一个支持 '?' 和 '*' 的通配符匹配。
'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串(包括空字符串)。
两个字符串完全匹配才算匹配成功。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 ? 和 *。
示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:
s = "aa"
p = "*"
输出: true
解释: '*' 可以匹配任意字符串。
示例 3:
输入:
s = "cb"
p = "?a"
输出: false
解释: '?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。
示例 4:
输入:
s = "adceb"
p = "ab"
输出: true
解释: 第一个 '' 可以匹配空字符串, 第二个 '' 可以匹配字符串 "dce".
示例 5:
输入:
s = "acdcb"
p = "a*c?b"
输出: false
看了之前的文章,我们就四步走吧
1.1. 动态规划组成部分1:确定状态
简单的说,解动态规划的时候需要开一个数组,数组的每个元素f[i]或者f[i][j]代表什么,类似数学题中x, y, z代表什么
wc,你倒是说说怎么确定要用动态规划来做啊?
看题目,需要逐步验证最长长度
没有时间复杂度空间复杂度限制,你可以选择>=On的
跟前面题很类似,这里需要考虑* 和 ?的情况。
尝试根据步骤写出转移方程
在这道题中,我们定义f[i][j] 表示字符串 s 的前 i 个字符与 字符串p的前 j 个字符是否匹配
解动态规划需要两个意识:
最后一步
子问题
最后一步
我们用示例来讲解 :s = "aaab" p = "aa*b"
根据题目意思,我们知道s和p要全匹配,我们直接用s去匹配p字符串的每一个字符,这样我们的最后一步就是用s字符串中的b字符去匹配p字符串的每一个字符,匹配最后一个字符为b是否相等。
子问题
这是 ' 动态规划Day two - 正则表达式匹配' 的子问题分析
有几种情况需要讨论,也就是用s去匹配p最后一个匹配的字符j
如果都是字符,只需要判断:f[i][j] = f[i-1][j-1]
如果是“.” ,说明可以匹配s的最后任意一个字符,也只需:
f[i][j] = f[i-1][j-1]
如果是“*”,分两种情况一种是匹配零个字符,一种是匹配1个或多个字符
如果是匹配零个字符:f[i][j] = f[i][j-2] ,因为如果j是*,我们就可以对p的j-1匹配任意次数,当然零次就是j-2了。
如果是匹配1个或多个字符:f[i][j] = f[i-1][j],匹配 s 末尾的一个字符,将该字符扔掉,而该组合还可以继续进行匹配,简单点说,零个我们判定了,如果是一个我们扔掉一个字符,如果能匹配则保存,如果匹配两个,我们是知道匹配s的上一个字符的结果的,直接匹配就行,同样匹配多个也是如此。(匹配多个是根据前一个的匹配结果得出来的)
这道题基本上是如出一辙
有几种情况需要讨论,也就是用s去匹配p最后一个匹配的字符j
如果都是字符,只需要判断:f[i][j] = f[i-1][j-1]
如果是“?” ,说明可以匹配s的最后任意一个字符,也只需:
f[i][j] = f[i-1][j-1]
如果是“”,分两种情况,第一种是不需要使用,第二种是需要使用*
实例 :s = "abc" p = "a*"。
在对s串的a遍历p串的*时,刚好满足dp[i][j] = dp[i][j-1] 此时i=1,j=2,
dp[1][2] = dp[1][1]=true。---不需要使用*
在对s串的b遍历p串的时,刚好满足dp[i][j] = f[i-1][j],因为是可以匹配任意一个字母的。
dp[2][2] = dp[1][2]=true。---需要使用*
在对s串的c遍历p串的时,刚好满足dp[i][j] = f[i-1][j],因为是可以匹配任意一个字母的。
dp[3][2] = dp[2][2]=true。---不需要使用*
1.2. 动态规划组成部分2:转移方程
转移方程可以详见子问题分析
1.3. 动态规划组成部分3:初始条件和边界情况
因为要涉及到i-1和j-1,注意边界
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0]=true
当f[0][j]时,需要判断j是否为*,因为*可以匹配null串
1.4. 动态规划组成部分4:计算顺序
用s串的每一个字符去匹配p串的每一个字符
它的时间复杂度是Onm,空间复杂度也是Onm
参考代码
public boolean isWildcardMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true;
for (int i = 1; i <= n; ++i) {
if (p.charAt(i - 1) == '*') {
dp[0][i] = true;
} else {
break;
}
}
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
} else if (p.charAt(j - 1) == '?' || s.charAt(i - 1) == p.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
}
}
}
return dp[m][n];
}
@Test
public void isisWildcardMatch() {
boolean i = isWildcardMatch("123", "1*");
Assert.assertNotNull(i);
}
No.9
这道题就很简单了,放松一下~👍👍👍👍
63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
\1. 向右 -> 向右 -> 向下 -> 向下
\2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
本题与
---
我是怎么向5岁侄女解释动态规划的?
---
里的不同路径1,大致相同,只是增加了障碍物,我们做一下没有障碍物的判断就行了。
2.1. 动态规划组成部分1:确定状态
最后一步
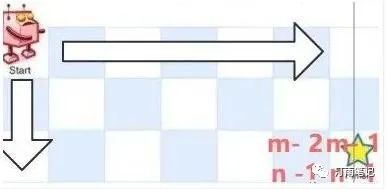
无论机器人用何种方式到达右下角,总有最后挪动的一步:-向右或者向下
如果所示,我们设右下角的坐标为(m-1,n-1)
那么最后一步的前一步机器人的位置在(m-2,n-1)或者(m-1,n-2)
子问题
那么,如果机器人有x种方式从左上角走到(m-2,n-1), 有Y种方式从左上角走到(m-1,n-2), 则机器人有X+Y的方式走到(m-1,n-1)
问题转化为,机器人有多少种 方式从左上角走到(m-2,n-1)或者(m-1,m-2)
如果走到是(m-2,n-1)如图:

我们可以直接干掉最后一列
同理如果是走到(m-1,n-2)行就减少一行。
状态:
设f[i][j]为机器人有多少种方式从左上角走到(i,j)
2.2. 动态规划组成部分2:转移方程
对于任意一个格子:
f[i][j] = f[i-1][j] + f[i][j-1]
1 2 3
1代表机器人有多少种方式走到[i][j]
2代表机器人有多少种方式走到f[i-1][j]
3代表机器人有多少种方式走到f[i][j-1]
2.3. 动态规划组成部分3:初始条件和边界情况
初始条件:f[0][0]=1,因为机器人只有一个方式到左上角
边界情况:i=0或j=0,则前一步只能有一个方向过来,也就是说第0行或者第0列,每走一步只有一种情况,则f[i][j] = 1,其他区域都满足转移方程。
如果遇到障碍物,f[i][j] = 0。
3.4. 动态规划组成部分4:计算顺序
按行计算,为什么按行计算呢?
对于这道题来说,按行计算在计算到f[1][1]时,f[0][1]和f[1][0]都已经计算了,同样按列计算这两坐标也计算了,不用再次计算。
f[0][0] = 1 如果第一个是障碍物f[0][0]=0
计算第0行:f[0][0],f[0][1],...,f[0][n-1]
计算第1行:f[1][0],f[1][1],...,f[1][n-1]
...
计算第m-1行:f[m-1][0],f[m-1][1],...,f[m-1][n-1]
时间复杂度:O(mn)
参考代码
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (obstacleGrid == null || obstacleGrid.length == 0) {
return 0;
}
// 定义 dp 数组并初始化第 1 行和第 1 列。
int m = obstacleGrid.length, n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
// 根据状态转移方程 dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 进行递推。
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
简单说一下滚动数组的版本,当我们知道当前位置的最多路径数时,我们去求下一个位置的路径数,只需要知道左边和上边的可以了,空间复杂度为o(m)
参考代码
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int n = obstacleGrid.length, m = obstacleGrid[0].length;
int[] f = new int[m];
f[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (obstacleGrid[i][j] == 1) {
f[j] = 0;
} else
if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
f[j] += f[j - 1];
}
}
}
return f[m - 1];
}
No.10
看到这次分享的最后一题啦,能看到这里的人呀,都是人才。❤️❤️❤️❤️
来一道比较简单的题目吧!!!
leecode 64. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。示例 2:
输入:grid = [[1,2,3],[4,5,6]] 输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
看了之前的题解,想想就明白了,这里用动态规划解题,考虑一下几点:
边界处理
中间的路径
这里的结果会有M*N次所以每个格子的结果都会作比较,我们取较小值就可以了
dp[i][j] 表示从左上角出发到 (i,j)(i,j) 位置的最小路径和 初始条件:dp[0][0]=grid[0][0]
当 i>0 j=0时dp[i][0]=dp[i-1][0] + grid[i][0]; // grid[i][0]为最后一个格子的值 当 i=0 j>0时dp[0][j-1]=dp[0][j-1] + grid[0][j]; 当 i>0 j>0时dp[i-1][j-1]=min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
参考代码:
class Solution {
public int minPathSum(int[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int rows = grid.length, columns = grid[0].length;
int[][] dp = new int[rows][columns];
dp[0][0] = grid[0][0];
for (int i = 1; i < rows; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int j = 1; j < columns; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (int i = 1; i < rows; i++) {
for (int j = 1; j < columns; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[rows - 1][columns - 1];
}
}
