图文并茂!动态规划热门题目剖析
作者 Chunel Feng,编程爱好者,阿里巴巴引擎开发工程师。
个人微信:ChunelFeng
个人博客:一面之猿网[1]
开源项目:Caiss 智能搜索引擎[2]
Doocs 开源社区的朋友们,你们好,我是 Chunel Feng[3]。今天,我们就来简单分析几道动态规划(Dynamic Programming,简称 DP)相关的热门面试题目,陪着大家一起熟悉或复习一下这一部分知识。
开始之前,我要首先声明我的态度:刷题绝不是为了进入大厂而必经的磨难,一个人的实力如何绝不可能仅通过几道算法题目得出结论。有目的的刷题,更多的为了提升对数据结构和算法的理解,扩宽编程的思路和方法。 这些经典的思路即便暂时无法受用在你的日常工作中,也可能在某个不经意的瞬间,在你的生活中熠熠生辉。
接下来我选的 4 道题目,分别代表 4 种类型:
•斐波那契数列•一维相邻动态规划•二维相邻动态规划•间隔动态规划
需要指出,有些题目我并没有给出最优解(我也会在题目后稍加说明),而是给出个人认为最容易理解、也最能契合特定 dp 类型的解法。个人水平有限,如果大家看出有什么不足,或者有更好的思路,希望随时交流指正。
一、爬楼梯
1. 题目链接:爬楼梯[4]
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数。示例1:输入:2输出:2解释:有两种方法可以爬到楼顶。1.1阶+1阶2.2阶
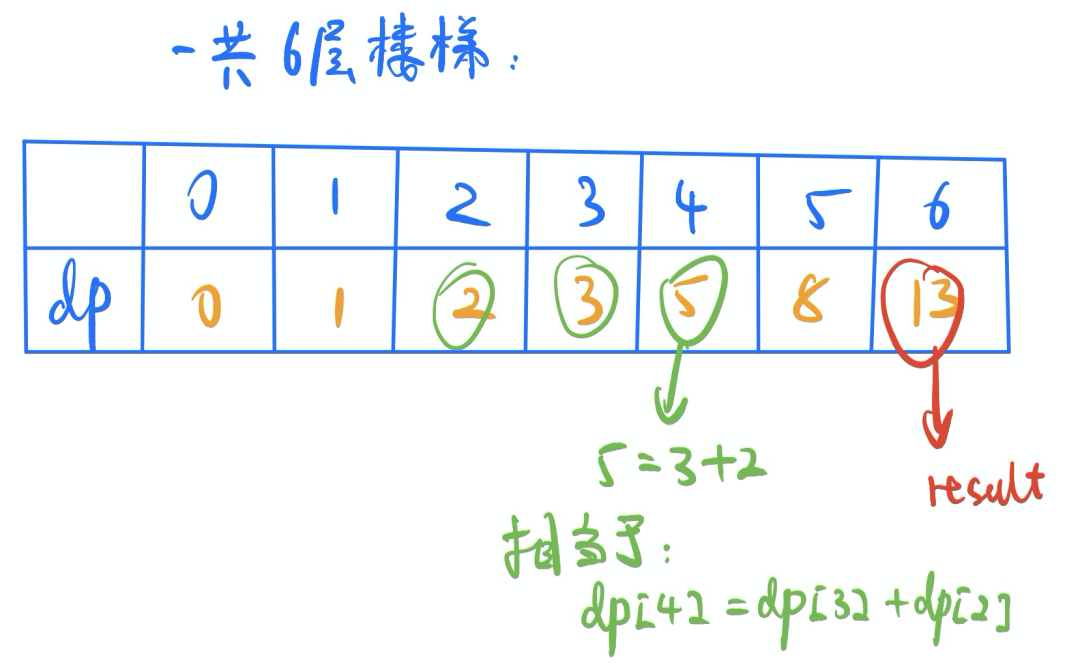
2. 解题思路
这是一个很典型的斐波那契数列问题,也是一个很适合dp入门的题目。爬到3楼,只有两种可能:先爬到1楼,然后再一步上两层;或者先爬到2楼,然后再一步上一层。故:爬到3楼的方法数,等于爬到【1楼】的方法数和爬到【2楼】的方法数之和。爬到4楼的方法数,等于爬到【2楼】的方法数和爬到【3楼】的方法数之和。从而很容易推到出: dp[i]= dp[i-1]+ dp[i-2]
3. 代码实现
classSolution{public:int climbStairs(int n){// 不考虑n小于2的临界值情况了vector<int> dp(n+1);dp[0]=0;dp[1]=1;dp[2]=2;for(int i =3; i <= n; i++){dp[i]= dp[i -1]+ dp[i -2];}return dp[n];}};
二、连续子数组的最大和
1. 题目链接:连续子数组的最大和[5]
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。示例1:输入:nums =[-2,1,-3,4,-1,2,1,-5,4]输出:6解释:连续子数组 [4,-1,2,1]的和最大,为 6。
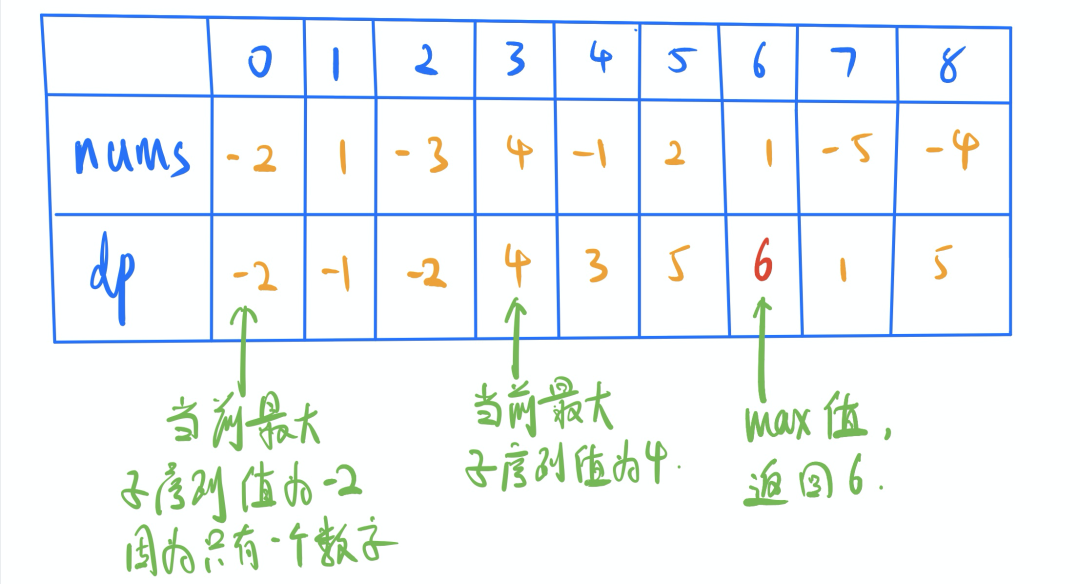
2. 解题思路
这一题更准确的说,应该是一个贪心的题目。在这里,用一维dp的方法来实现。也是在一定程度上,说明一维dp和贪心之间,有一定的关联关系。解题思路,主要就是设定一个一维dp数组,数组的每一位记录当前最大的子序列值。体现在图中,就是dp[3]= max(4,-2+4)=4;dp[6]= max(5,1+5)=6;dp[i]= std::max(dp[i-1]+ nums[i], nums[i]);如果有超过之前最大值的,则更新result值。
3. 代码实现
classSolution{public:int maxSubArray(vector<int>& nums){vector<int> dp(nums.size());dp[0]= nums[0];int result = dp[0];for(int i =1; i < nums.size(); i++){dp[i]= std::max(dp[i-1]+ nums[i], nums[i]);result = std::max(dp[i], result);}return result;}};
4. 补充说明
以上给出的解法,更偏向贪心和动态规划的结合。还有一种dp方法,是在dp数组中的每个值,均记录当前为止最大的子序列和是多少,然后返回dp[len-1]即可。
三、礼物的最大价值
1. 题目链接:礼物的最大价值[6]
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?示例1:输入:[[1,3,1],[1,5,1],[4,2,1]]输出:12解释:路径1→3→5→2→1可以拿到最多价值的礼物
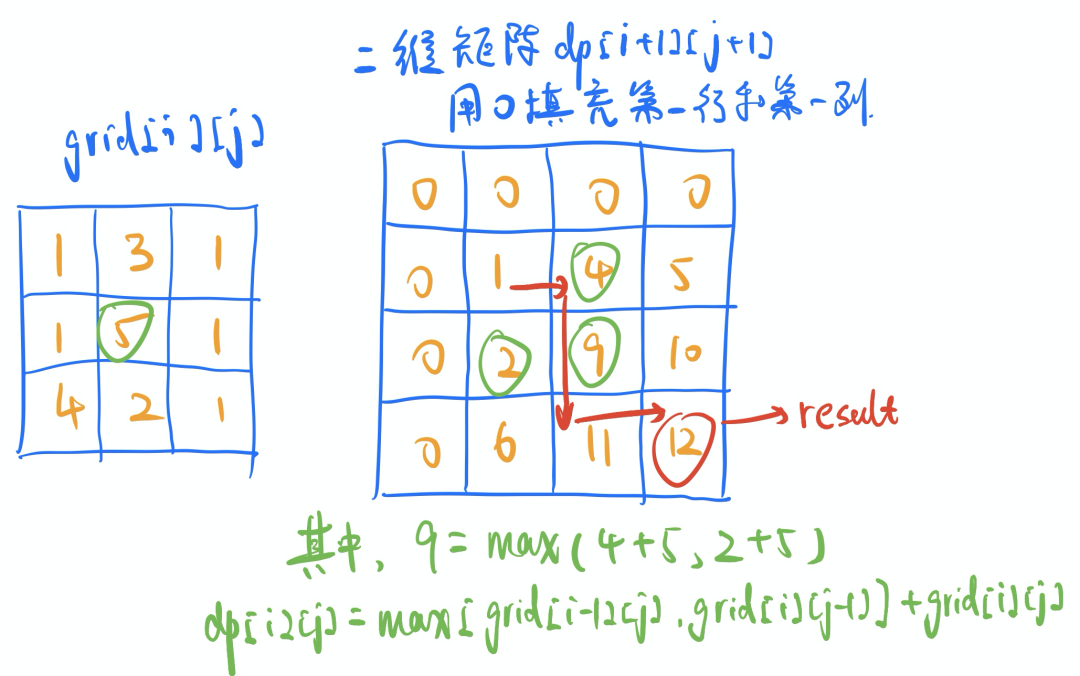
2. 解题思路
这是一道典型的二维动态规划的题目。dp[i][j]值表示的表示的就是,走到当前位置,最多可以拿到的礼物价值之和。在计算dp[i][j]的过程中,该值总是与grid[i-1][j-1]、dp[i-1][j]、dp[i][j-1]相关。dp[2][2]= max(dp[1][2], dp[2][1])+ grid[1][1];dp[2][3]= max(dp[1][3], dp[2][2])+ grid[1][2];dp[i][j]= max(dp[i-1][j], dp[i][j-1])+ grid[i-1][j-1];体现在图中,就是9= max(4+5,2+5)。依次计算下去,dp矩阵右下角的值(12),即为所求。而红色的箭头,表示的就是前进的方向。
3. 代码实现
classSolution{public:int maxValue(vector<vector<int>>& grid){int h = grid.size();// 行数int w = grid[0].size();// 列数if(h ==0|| w ==0){return0;}// 生成一个二维的dp数组vector<vector<int>> dp(h+1, vector<int>(w+1,0));for(int i =0; i < h+1; i++){for(int j =0; j < w+1; j++){if(i !=0&& j !=0){// 第0行和第0列值均为0,不参与计算。dp[i][j]= max(dp[i-1][j], dp[i][j-1])+ grid[i-1][j-1];}}}return dp[h][w];}};
4. 补充说明
需要说明的是,这种解法相对比较容易理解,但在空间复杂度上有一定的优化空间。当计算dp[i][j]的值的时候,其实仅用到了i行和i-1行的数据。故计算的时候,可以仅保留上一行数据,甚至是上一行中涉及到的个别数据。具体方法,大家可以自己百度一下,当做一个知识点扩展了吧。
5. 相似推荐
类似的问题,给大家推荐 leetcode中【72.编辑距离】。需要说明的一点是,编辑距离的计算过程中,还有一些可以减少时间复杂度的彩蛋哦,大家自己去发掘哈。
四、零钱兑换
1. 题目链接:零钱兑换[7]
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。你可以认为每种硬币的数量是无限的。示例 1:输入:coins =[1,2,5], amount =11输出:3解释:11=5+5+1
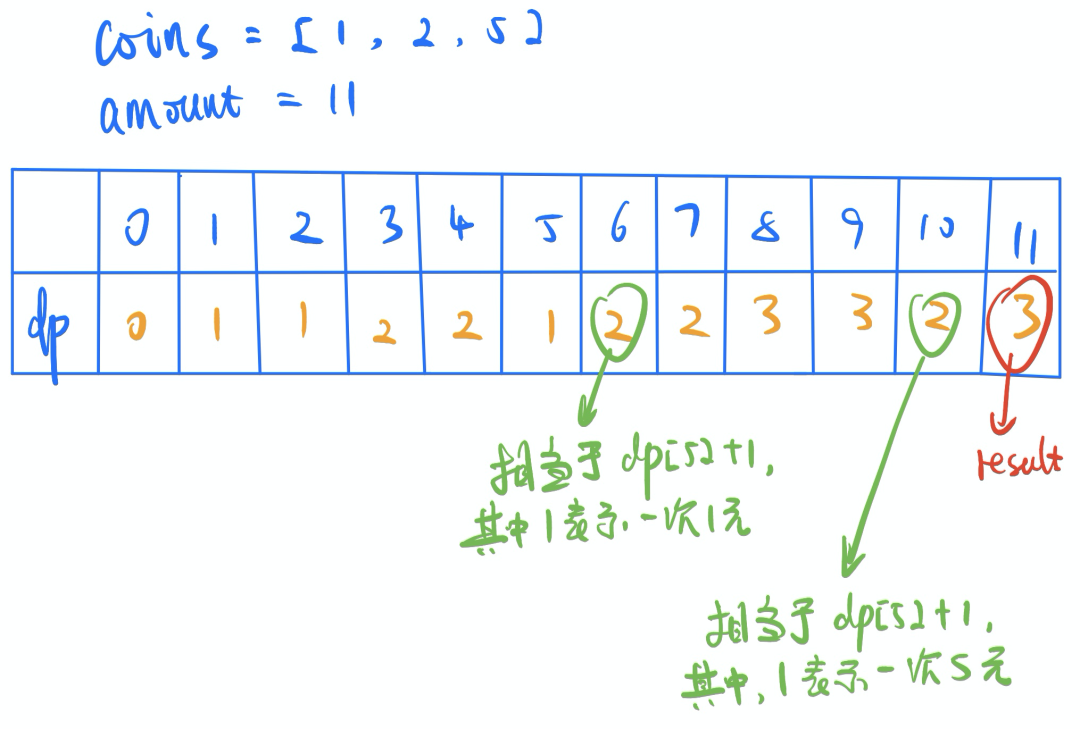
2. 解题思路
找零问题,也是属于比较经典的一种 dp 问题。相比于上面几道题目,这一题的不同点在于,这里的 dp[i]并不是与自己相邻的 dp[i-1]产生关系。需要根据零钱的面额,向前找k个值(体现在 dp[i]= dp[i-coins[j]]+1这一句代码里)。
3. 代码实现
classSolution{public:int coinChange(vector<int>& coins,int amount){vector<int> dp(amount+1,-1);// 所有数据,默认用-1占位,表示没有被计算过dp[0]=0;for(int i =1; i <= amount; i++){for(int j =0; j < coins.size(); j++){/* 如果当前面值小于i,并且i-coins[j]面额的钱也可以被拼出。比如dp[7]和2块钱面额,并且 dp[7-2]!=-1*/if(coins[j]<= i && dp[i-coins[j]]!=-1){/* 内部循环,如果dp[i]未被计算过,或者出现更低的值,则更新dp[i]的值 */if(dp[i]==-1|| dp[i]> dp[i-coins[j]]+1){dp[i]= dp[i-coins[j]]+1;}}}}return dp[amount];}};
4. 补充说明
上面是的解法,如果提前将coins中的值进行排序,还可以进行一些剪枝逻辑。比如,当一旦发现 coins[j]>i,则结束内部的循环。这个主要是为了说明,动态规划中合理的加入剪枝方法,可以一定程度的降低计算的时间复杂度。
5. 相似推荐
类似的问题,给大家推荐:背包问题。背包问题,更像是找零问题的二维版本,加入了重量和价值两个影响因素。具体问题就不给大家罗列了,自行百度一下或者去B站上搜,会有很多。记得要看哦。
结束语
由于工作性质的关系,我时而会需要去实现或优化一些相对复杂的算法和数据结构。每每这个时候,之前刷 Leetcode 的一些经验和心得,就会让我觉得受益匪浅。所以,即便没有换工作的诉求,我也会偶尔抽一点时间尝试去写几道题目。现在比较流行的一些深度学习算法,本质上也就是通过动态调整参数的方式去求最优解的过程。
动态规划应该属于 Leetcode 中相对比较难的题目了,没有做过的小白,无从下手是很正常的。从上面几道题目可以看出,dp 相关的题目代码量一般都不大,如果能抽象出其中关系,保持清晰思路,coding 起来并不难。不过,写了几道题并不代表就学通了 dp 的精髓,出现“今天刷了明天忘”的情况也都是很正常的。学着感受动态规划的思路,学着把一个复杂的问题拆解成一些简单且有关联问题的,然后逐个击破并获取最优解,这才是重点。
其实,不仅在刷题中,在日常的工作中,在面对生活中的各种复杂事情时,我们更应该有这种化繁为简、并且一步一个脚印的去做的思路才对啊。
引用链接
[1] 一面之猿网: http://www.chunel.cn[2] Caiss 智能搜索引擎: https://github.com/ChunelFeng/caiss[3] Chunel Feng: https://github.com/ChunelFeng[4] 爬楼梯: https://leetcode-cn.com/problems/climbing-stairs/[5] 连续子数组的最大和: https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/[6] 礼物的最大价值: https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/[7] 零钱兑换: https://leetcode-cn.com/problems/coin-change/
长按识别下图二维码,关注公众号「Doocs 开源社区」,第一时间跟你们分享好玩、实用的技术文章与业内最新资讯。
