动态规划:特朗普怎样才能赢?
美国大选正在如火如荼进行当中,假如你是特朗普的竞选助手,大选前要去各州开展竞选宣传活动,但是现在你只有10天时间,没有办法每个州都去,需要根据各州的重要性和时间花费拿出一套方案,否则就将被特朗普fire掉。

假设每个州初始情况都是中立的,只要去开展宣传活动就能获得选票,每个州的选举人票数是不一样的,但是票数越多的州需要花费的时间也越多,在时间有限的情况下,你该怎么安排行程,让竞选的胜算更大呢?
下面是每个州的选举人票数:
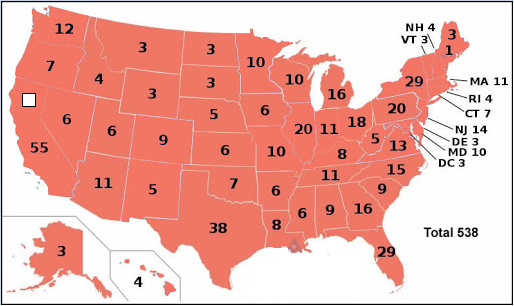
为了把问题简化,我们这里只考虑取选票数前10的州,time字段表示去这个州宣传活动所需的时间,单位是天:
all_states = [
{'name':'加利福尼亚州', 'votes':55, 'time':5},
{'name':'德克萨斯州', 'votes':38, 'time':3},
{'name':'佛罗里达州', 'votes':29,'time':2},
{'name':'纽约州', 'votes':29, 'time':2},
{'name':'伊利诺伊州', 'votes':20, 'time':1},
{'name':'宾西法利亚州', 'votes':20,'time':1},
{'name':'俄亥俄州','votes':18,'time':1},
{'name':'密歇根州','votes':16,'time':1},
{'name':'乔治亚州', 'votes':16,'time':1},
{'name':'北卡罗来纳州', 'votes':15,'time':1}
]
递归求解
第一种办法,递归求解。
对于每一个州,你有两种选择:去或者不去。
如果去,则获得的选票是:这个州的选票 + 剩下时间里去剩下州能获得的最多票数
如果不去,则获得的选票是:剩下时间(这一次不去就没花时间)里去剩下州能获得的最多票数。
最后,比较去或者不去的结果,选择更优的方案。
这里,把剩下时间里去剩下州能获得的最多票数定义为一个函数,随着上面问题的拆解,不断递归:
# 递归解决
# 在指定索引后的州中,剩余时间内,能获得的最多选票
def recurse_solution(states, index, time):
if len(states) == 0 or index >= len(states) or time <= 0:
return 0
# 去这个州(时间还够的话)
a = 0
if states[index]['time'] <= time:
a = states[index]['votes'] + recurse_solution(states, index + 1, time-states[index]['time'])
# 不去这个州
b = recurse_solution(states, index + 1, time)
return max(a, b)
def main():
print("max votes: %d" % recurse_solution(all_states, 0, 10))
记忆化搜索
上面的递归过程,如同一个二叉树,从根节点不断分叉成:去 / 不去 两个分支,直到叶子节点(剩下州或剩下时间为0)。
然后选出各个路径中和最大的那一条。
递归求解会有很多重叠子问题,就如同那个二叉树中会有很多重叠的子树,重复计算浪费很多时间。
新的方案中引入一个记忆存储memo,定义为指定索引后的州中,剩余时间内,能获得的最多选票,每次计算完后将其记录在案,后续遇到直接查表,不再重复计算:
# 引入记忆化搜索
# memo[index][time]: 在指定索引后的州中,剩余时间内,能获得的最多选票
memo = [[0 for i in range(100)] for j in range(100)]
def memo_search_solution(states, index, time):
if len(states) == 0 or index >= len(states) or time <= 0:
return 0
# 如果记忆表中存有历史结果,直接使用
if memo[index][time] != 0:
return memo[index][time]
# 去这个州(时间还够的话)
a = 0
if states[index]['time'] <= time:
a = states[index]['votes'] + memo_search_solution(states, index + 1, time-states[index]['time'])
# 不去这个州
b = memo_search_solution(states, index + 1, time)
# 记录这次结果,供下次使用
memo[index][time] = max(a, b)
return max(a, b)
def main():
print("max votes: %d" % memo_search_solution(all_states, 0, 10))
动态规划
上面的递归和引入记忆化搜索后的递归,都是自顶向下的思考这个问题:在去与不去两种方案中选择。接着再继续在子问题中再次思考去与不去。
而动态规划则调转枪头,自下而上。
先解决只有1个州,只有1天时间,能获得的最大选票
再解决有2个州,只有1天时间,能获得的最大选票
···
再解决全部州,只有1天时间,能获得的最大选票
再解决全部州,有2天时间,能获得的最大选票
···
最后解决全部州,有10天时间,能获得的最大选票
如同正在进行的人口普查,下面每个街道的数据知道了,想知道这个区县的数据就容易了。
知道了每个区县的数据,想知道这个市的数据就容易了。
知道了每个市的数据,想知道这个省的就容易了。
以此类推。
## 动态规划解决
def dp_solution(states, time):
# memo[index][time]: 在指定索引后的州中,剩余时间内,能获得的最多选票
memo = [[0 for i in range(time+1)] for j in range(len(states)+1)]
for i in range(1, len(states) + 1):
for j in range(1, time+1):
if states[i - 1]['time'] <= j:
# 如果时间还够
# 选择不去
a = memo[i-1][j]
# 选择去
b = memo[i-1][j-states[i-1]['time']] + states[i-1]['votes']
# 记录去和不去两种选择的最优值
memo[i][j] = max(a, b)
else:
# 如果时间不够
memo[i][j] = memo[i-1][j]
return memo[len(states)][time]
def main():
print("max votes: %d" % dp_solution(all_states, 10))
执行上面的代码输出:
max votes: 157
通过上面的代码能够知道特朗普能够获得的最多选票数:157张。
你高高兴兴的告诉特朗普:“Hi,Trump,这10天的宣传活动,你最多能获得157张选票”
但是现在特朗普问你:“去哪些州?行程怎么安排”
你支支吾吾半天没答出来。
特朗普见状说到:“还是让我亲自来,没有人比我更懂动态规划”
