【数据挖掘】特征相关性挖掘神器-线性非线性关系一键挖掘！

简 介

很多时候，我们在计算特征之间相关性或者绘制相关性矩阵的时候习惯性地会使用Pearson相关性，这在诸多问题中确实可以为模型预测等方面带来很多帮助，但它却存在着下面三个比较大的问题：

1. 考虑的是特征之间的线性关系，如果绝对值越大，那么两个变量之间的线性相关性就越强，反之线性关系就越低；如果两个变量之间存在极强的非线性关系，也会因为线性关系较低，而被误以为没什么关系；

2. 没法同时适用于类别变量和数值变量的关系计算，或者计算得到的分数价值也不大；
3. 相关性系数矩阵是对称的，而在许多问题中我们特征变量之间的关系并不一定是对称的；

那么有没有一种方法可以同时缓解上面的几个问题呢？有的！就是本文介绍的PPS(Predictive Power Score)。

Predictive Power Score

假设我们有两个变量，想要计算变量预测的能力，我们通过下面的方式进行计算：

• 将变量作为目标变量，将作为特征；
• 使用决策树进行交叉验证，并依据评估指标计算得到分数cross_score;
• 当变量为数值型，我们使用Decision Tree Regressor并计算MAE);
  
• 当变量为类别型，我们使用Decision Tree Classifier并计算weighted F1);
  
• 计算的值作为我们最终的分数;
• 分类问题：final_score = (cross_score - naive_score)/(1-naive_score)，这里naive_score是出现最多的类作为最终预测结果计算得到的分数；，使用中位数作为最终预测结果计算得到的分数；
• 回归问题：final_score = 1 - (cross_score / naive_mae)，这里naive_score是使用中位数作为最终预测结果计算得到的分数；

代码

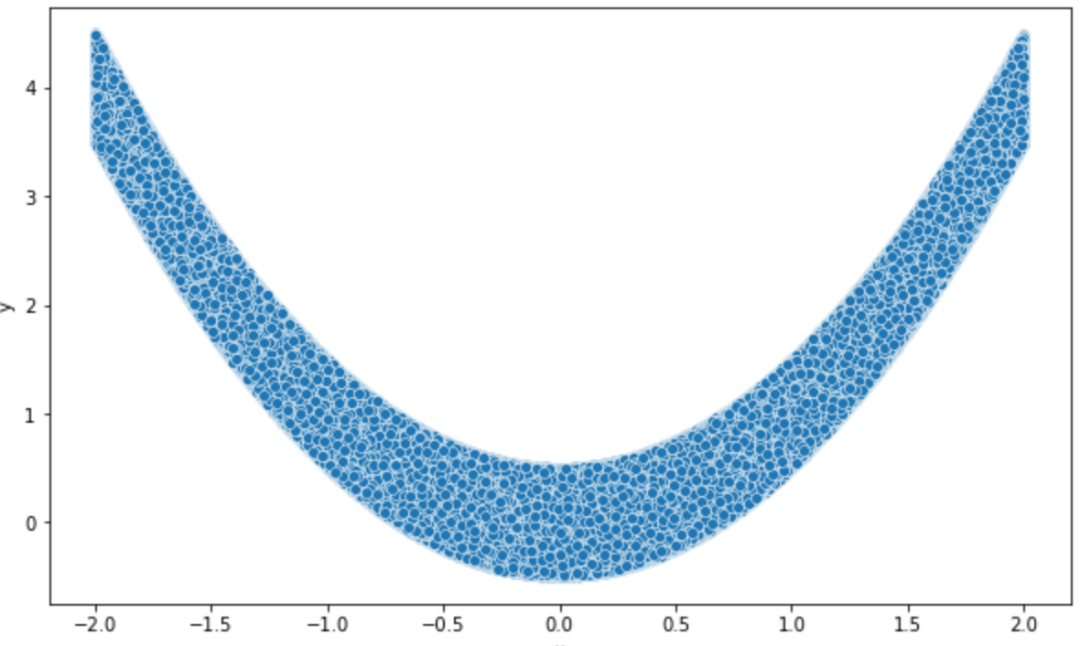
此处我们构建一个二次关系：特征从-2到2的均匀变量，目标是的平方加上一些误差,perfect是的平方。

import pandas  as pd
import numpy   as np
# !pip install -U ppscore
import ppscore as pps
import matplotlib.pyplot as plt
import seaborn as sns
df          = pd.DataFrame()
df["x"]     = np.random.uniform(-2, 2, 1_000_000)
df["error"] = np.random.uniform(-0.5, 0.5, 1_000_000)
df["y"]     = df["x"] * df["x"] + df["error"]
df["y_perfect"]     = df["x"] * df["x"] 

plt.figure(figsize=[10,6])
sns.scatterplot(x = 'x', y ='y', data=df) 

<AxesSubplot:xlabel='x', ylabel='y'>

1.对称性分析

• 变量的分数是不一样的，非对称的；

pps.score(df, "x", "y")

{'x': 'x',
 'y': 'y',
 'ppscore': 0.6698987690580689,
 'case': 'regression',
 'is_valid_score': True,
 'metric': 'mean absolute error',
 'baseline_score': 1.0177846519084408,
 'model_score': 0.3359719664287812,
 'model': DecisionTreeRegressor()}

pps.score(df, "y", "x")

{'x': 'y',
 'y': 'x',
 'ppscore': 0,
 'case': 'regression',
 'is_valid_score': True,
 'metric': 'mean absolute error',
 'baseline_score': 1.0030129309668745,
 'model_score': 1.0892163726367778,
 'model': DecisionTreeRegressor()}

2.可视化

• 基于PPS的相关性矩阵

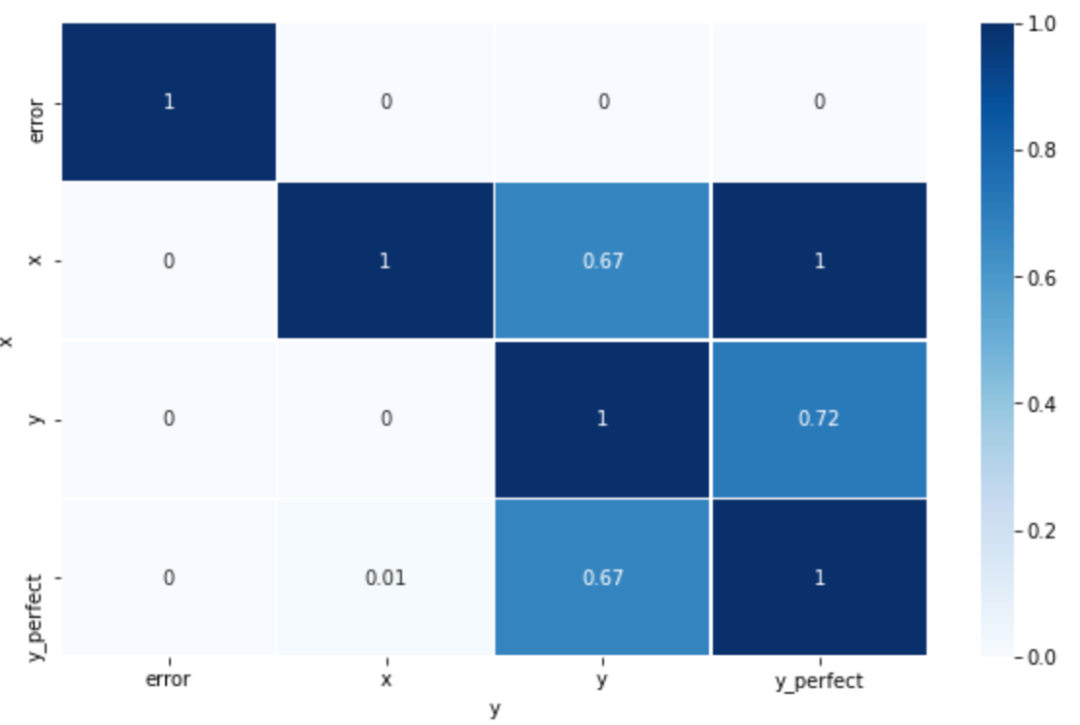
plt.figure(figsize=[10,6])
matrix_df = pps.matrix(df)[['x', 'y', 'ppscore']].pivot(columns='y', index='x', values='ppscore')
sns.heatmap(matrix_df, vmin=0, vmax=1, cmap="Blues", linewidths=0.5, annot=True)

<AxesSubplot:xlabel='y', ylabel='x'>

• 基于Person相关系数的相关性矩阵

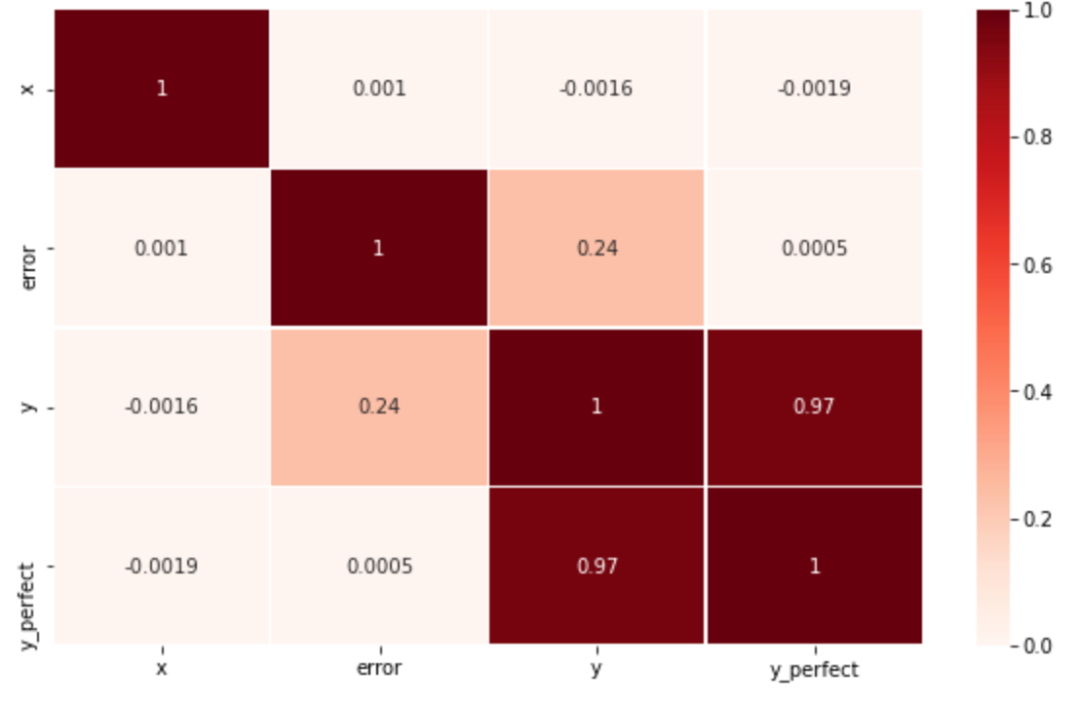
plt.figure(figsize=[10,6])
sns.heatmap(df.corr(), vmin=0, vmax=1, cmap="Reds", linewidths=0.5, annot=True)

<AxesSubplot:>

3.小结

从上面的分析我们可以发现：

• 基于Person相关系数的方法完全没有找到与的潜在关系；
• 给予PPS的方法则完美的找到了与以及perfect的关系。

适用问题

PPS的方法适用的问题非常多，应用的方面也很广，此处我们将其归纳为下面几点：

• 数据分析：PPS的方式可以表示两个数据之间的潜在关系（线性的非线性的），PPS的相关性图是非常好的一种可视化的解释方式；
• 特征筛选，其特征筛选的方式和Pearson相关性的方式类似，如果我们变量与标签之间的PPS分数很低的话，那么该特征可能和我们的目标变量并不存在任何关系，包括线性的和非线性的关系，可以考虑直接删除处理；
• 信息泄漏：使用PPS矩阵检测变量之间的信息泄漏-信息泄漏是通过其他变量导致的。

当然因为PPS是基于模型(目前主要是决策树相关的模型)计算得到的，所以它也带来了一些劣势：

• 计算时间更高；
• PPS的分数无法像相关性那样容易解释（线性相关性的PPS可能为1，二次关系的PPS也可能为1），所以PPS更适合于发现模式；
• 无法用严格的数学方法比较不同目标变量的得分，它们是使用不同的评估指标计算得到的；
• 目前的PPS是基于决策树为主的模型进行计算的，所以决策树的劣势也会在PPS计算中存在；

参考文献

1. Predictive Power Score vs Correlation
2. Correlation Vs Predictive Power Score
3. RIP correlation. Introducing the Predictive Power Score
4. https://github.com/8080labs/ppscore