2022年11月温州一模第15题解析
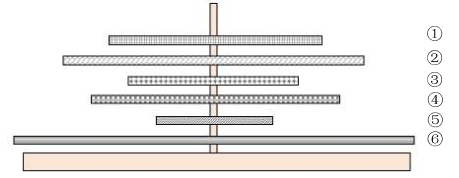
队列和栈是非常重要的两种数据结构,教材也安排了大量的篇幅来介绍这两种数据结构的基本特征和基本操作,因此它们的基本特征和操作肯定是要考的。
但是如何在编程题中考查队列和栈的应用?它会考到何种难度?我们该教到何种程度?这就让老师们犯了难。因为涉及到队列和栈的算法题都不简单,一不小心就会进入到广搜和深搜等较为复杂的领域。
命题老师们一直在模糊的边界摸索,试图找到一些既能考查队列和栈的基本操作,又不涉及复杂算法的案例,绞尽脑汁、用心良苦,为大家在前方趟雷,逐步拓展命题的边界。
2022年11月温州一模第15题



数组、字典、栈的基本操作,自定义函数和查找最值算法。要求学生理解字典的表示方法,熟练掌握栈的基本操作。
题目的问题是计算拿走几片圆盘后,能看到的圆盘颜色种数最多?但程序实现并没有模拟拿走圆盘的过程,而是逆向思维,观察从下往上逐渐堆叠圆盘时,最多能看到几种颜色。
为了找到最优解,程序构造了一个栈,用来存储能够被看到的圆盘编号,因为圆盘入栈的顺序是从下往上,为了确保栈中圆盘都能被看到,则其半径值必须是一个递减序列。所以每次将编号为i的圆盘入栈时,必须先将半径小于r[i]的元素退栈。
此外,因为题目要求的不是最多能看到的圆盘数量,而是最多能看到的颜色种类,故相同颜色的圆盘只能算1个。为此程序创建了一个字典f,用来存储某种颜色对应的圆盘数量。当有元素退栈时,当前可见颜色数量cnum不一定会减少,只有当某种颜色的圆盘数量为0时,才将cnum的值减1。这就是第①空的算法原理。
新圆盘入栈后,cnum的值不一定会加1,只有当f中不包含栈顶圆盘颜色时,才将cnum的值加1,否则只让该颜色对应的圆盘数量加1。接下来判断cnum是否为最优解,若为最优解,则更新存储最优解的变量cmax、res和m——它们分别存储了最大可见颜色数量、可见颜色种类及其对应圆盘数量(注意不能写作res=f,否则res与f会指向同一对象)和拿走圆盘的数量。
搞清楚算法原理以后,各问题的答案就呼之欲出了:
圆盘i入栈前,先要将半径小于r[i]的圆盘出栈,以保持栈中元素的递减特性。故函数pop()的作用是将半径小于rad的圆盘出栈,返回新的栈顶指针(top)和可见的颜色数量(cnum)。
color[z[top]]表示栈顶圆盘的颜色,圆盘出栈后,其所属颜色的圆盘数量要减1,即f[color[z[top]]] -= 1。当该种颜色的圆盘数量为0时,需要将cnum的值减1。由此得到第①空的答案f[color[z[top]]] == 0。
第②空语句的功能是将编号为i的圆盘入栈,即z[top] = i。
第③空是计算被拿走圆盘的数量,因为此时叠放的圆盘数量为(i+1),故m=n-(i+1)。
为代码添加注释如下图所示:
(1)将半径小于rad的圆盘出栈,返回新的栈顶指针(top)和可见的颜色数量(cnum)。
(2)① f[color[z[top]]] == 0
② z[top] = i
③ m=n-(i+1)
此题程序采用逆序思维,逐个叠加圆盘数量,并通过维护一个递减栈来记录可见圆盘编号,以便快速计算可见颜色数量,使用字典f来记录当前可见颜色种类及其对应圆盘数量信息,构思非常巧妙。
正因为程序的技巧性太强,引入了较多的变量,代码实现蜿蜒曲折,不够直观,增加了阅读难度,学生得分率很低。
我们也可以采用正向思维,直接模拟拿走圆盘的过程。计算有哪些圆盘可以看到,就好比寻找一个递增序列。我们通过遍历r[i:],寻找以r[i]为首元素的递增序列;并创建列表c,用c[i]存储以圆盘i为顶盘时的可见颜色字符串,每当递增序列中出现一种新颜色的圆盘,将该颜色添加到c[i]中。
当出现最优解时,可设置m = i,则不仅可以用m表示拿走圆盘的数量,还可以用c[m]表示最大可见颜色字符串。
实现相关功能的程序代码如下,请将缺失的代码补充完整:
r = [5, 8, 4, 6, 3, 9] # 从上向下依次给圆盘编号0,1,2,...
color = ['红', '橙', '绿', '蓝', '紫', '红']
n = len(r)
print("序号\t半径\t颜色\t")
for i in range(1, n+1):
print(f"{i}\t{r[i-1]}\t{color[i-1]}\t")
c = [] # c[i]是一个字符串,记录了以盘子i为顶盘时的可见颜色
m = 0
for i in range(n):
c.append(color[i]) # 记录能看见的盘子颜色
p = i # 当前能看见的盘子下标
for j in range(i+1, n): # 寻找以r[i]为首元素的递增序列
if r[j] > r[p]:
p = ①
if ②:
c[i] += color[j]
if len(c[i]) > len(c[m]):
m = ③
print("拿走", m, "片后,可看到圆盘的颜色种数最多,分别为: ", c[m])
① j
② color[j] not in c[i]
③ m = i
为了保证解析的原创性和思维的独特性,我都是独立解题后,先不看答案(除非题目不会做),直接把解析写好,再去看答案。
当然,如果发现参考答案有更好的思路,我还是很乐于学习和借鉴的。同时,由于本人水平有限,解析中难免出现疏漏甚至错误之处,敬请谅解。
无论是赞同还是反对我的看法,都请你给我留言。如果你有新的想法,千万不要憋在心里,请发出来大家一起讨论。让我们相互学习,共同进步!
需要本文word文档、源代码和课后思考答案的,可以加入“Python算法之旅”知识星球参与讨论和下载文件,“Python算法之旅”知识星球汇集了数量众多的同好,更多有趣的话题在这里讨论,更多有用的资料在这里分享。
我们专注Python算法,感兴趣就一起来!
相关优秀文章:
