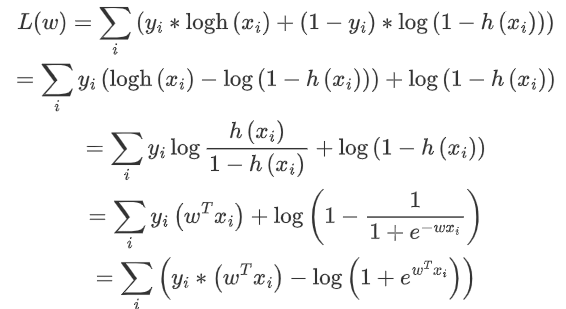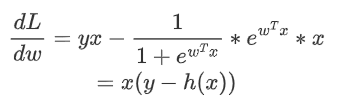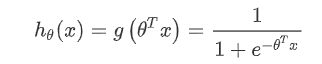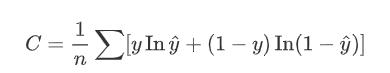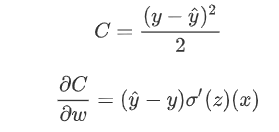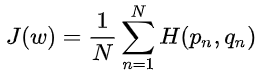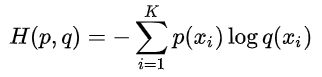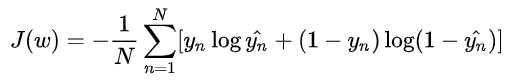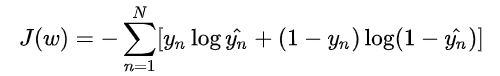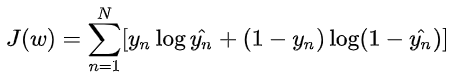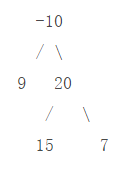21年7月底，字节推荐算法（DATA-EDU）面试题10道

问题1：bert蒸馏了解吗

知识蒸馏的本质是让超大线下  teacher model来协助线上student model的training。

bert的知识蒸馏，大致分成两种。

第一种，从transformer到非transformer框架的知识蒸馏

这种由于中间层参数的不可比性，导致从teacher model可学习的知识比较受限。但比较自由，可以把知识蒸馏到一个非常小的model，但效果肯定会差一些。

第二种，从transformer到transformer框架的知识蒸馏

由于中间层参数可利用，所以知识蒸馏的效果会好很多，甚至能够接近原始bert的效果。但transformer即使只有三层，参数量其实也不少，另外蒸馏过程的计算也无法忽视。
所以最后用那种，还是要根据线上需求来取舍。


问题2：给你一些很稀疏的特征，用LR还是树模型
参考：很稀疏的特征表明是高维稀疏，用树模型（GBDT）容易过拟合。建议使用加正则化的LR。
假设有1w 个样本， y类别0和1，100维特征，其中10个样本都是类别1，而特征 f1的值为0，1，且刚好这10个样本的 f1特征值都为1，其余9990样本都为0(在高维稀疏的情况下这种情况很常见)，我们都知道这种情况在树模型的时候，很容易优化出含一个使用 f1为分裂节点的树直接将数据划分的很好，但是当测试的时候，却会发现效果很差，因为这个特征只是刚好偶然间跟 y拟合到了这个规律，这也是我们常说的过拟合。但是当时我还是不太懂为什么线性模型就能对这种 case 处理的好？照理说 线性模型在优化之后不也会产生这样一个式子：y = W1*f1 + Wi*fi+….，其中 W1特别大以拟合这十个样本吗，因为反正 f1的值只有0和1，W1过大对其他9990样本不会有任何影响。
现在的模型普遍都会带着正则项，而 lr 等线性模型的正则项是对权重的惩罚，也就是 W1一旦过大，惩罚就会很大，进一步压缩 W1的值，使他不至于过大，而树模型则不一样，树模型的惩罚项通常为叶子节点数和深度等，而我们都知道，对于上面这种 case，树只需要一个节点就可以完美分割9990和10个样本，惩罚项极其之小.
这也就是为什么在高维稀疏特征的时候，线性模型会比非线性模型好的原因了：带正则化的线性模型比较不容易对稀疏特征过拟合。


问题3：LR的损失函数推导
 逻辑回归损失函数及梯度推导公式如下：

求导：


问题4：为什么分类用交叉熵不用MSE（从梯度的角度想一下）
LR的基本表达形式如下：
使用交叉熵作为损失函数的梯度下降更新求导的结果如下：

首先得到损失函数如下：
如果我们使用MSE作为损失函数的话，那损失函数以及求导的结果如下所示：
使用平方损失函数，会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。使用交叉熵的话就不会出现这样的情况，它的导数就是一个差值，误差大的话更新的就快，误差小的话就更新的慢点，这正是我们想要的。

在使用 Sigmoid 函数作为正样本的概率时，同时将平方损失作为损失函数，这时所构造出来的损失函数是非凸的，不容易求解，容易得到其局部最优解。如果使用极大似然，其目标函数就是对数似然函数，该损失函数是关于未知参数的高阶连续可导的凸函数，便于求其全局最优解。（关于是否是凸函数，由凸函数的定义得，对于一元函数，其二阶导数总是非负，对于多元函数，其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵）


问题5：BERT和Roberta的区别
RoBERTa 模型在 Bert 模型基础上的调整：
训练时间更长，Batch_size 更大，（Bert 256，RoBERTa 8K）
训练数据更多（Bert 16G，RoBERTa 160G）
移除了 NPL（next predict loss）
动态调整 Masking 机制
Token Encoding：使用基于  bytes-level 的 BPE

简单总结如下：



问题6：分词方法BPE和WordPiece的区别
BPE与Wordpiece都是首先初始化一个小词表，再根据一定准则将不同的子词合并。词表由小变大

BPE与Wordpiece的最大区别在于，如何选择两个子词进行合并：BPE选择频数最高的相邻子词合并，而WordPiece选择能够提升语言模型概率最大的相邻子词加入词表。
 


问题7：残差网络有哪些作用？除了解决梯度消失？
解决梯度消失和网络退化问题。

残差网络为什么能解决梯度消失？

残差模块能让训练变得更加简单，如果输入值和输出值的差值过小，那么可能梯度会过小，导致出现梯度小时的情况，残差网络的好处在于当残差为0时，改成神经元只是对前层进行一次线性堆叠，使得网络梯度不容易消失，性能不会下降。
 
什么是网络退化？

随着网络层数的增加，网络会发生退化现象：随着网络层数的增加训练集loss逐渐下降，然后趋于饱和，如果再增加网络深度的话，训练集loss反而会增大，注意这并不是过拟合，因为在过拟合中训练loss是一直减小的。

残差网络为什么能解决网络退化？

在前向传播时，输入信号可以从任意低层直接传播到高层。由于包含了一个天然的恒等映射，一定程度上可以解决网络退化问题。


问题8：交叉熵损失，二分类交叉熵损失和极大似然什么关系？
什么是交叉熵损失？

机器学习的交叉熵损失函数定义为：假设有N个样本，
其中：
从一个直观的例子感受最小化交叉熵损失与极大似然的关系。
去掉 1/N 并不影响函数的单调性，机器学习任务的也可以是最小化下面的交叉熵损失：
等价于最大化下面这个函数：
 不难看出，这其实就是对伯努利分布求极大似然中的对数似然函数(log-likelihood)。
也就是说，在伯努利分布下，极大似然估计与最小化交叉熵损失其实是同一回事。

可参考：https://zhuanlan.zhihu.com/p/51099880


问题9：二叉树最大路径和（路径上的所有节点的价值和最大）
方法一：递归

首先，考虑实现一个简化的函数 maxGain(node)，该函数计算二叉树中的一个节点的最大贡献值，具体而言，就是在以该节点为根节点的子树中寻找以该节点为起点的一条路径，使得该路径上的节点值之和最大。
具体而言，该函数的计算如下。
空节点的最大贡献值等于 00。
 
非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和（对于叶节点而言，最大贡献值等于节点值）。
 
例如，考虑如下二叉树。
叶节点 99、1515、77 的最大贡献值分别为 99、1515、77。


得到叶节点的最大贡献值之后，再计算非叶节点的最大贡献值。节点 2020 的最大贡献值等于 20+max(15,7)=35，节点 -10 的最大贡献值等于 -10+max(9,35)=25。
上述计算过程是递归的过程，因此，对根节点调用函数 maxGain，即可得到每个节点的最大贡献值。
 
根据函数 maxGain 得到每个节点的最大贡献值之后，如何得到二叉树的最大路径和？对于二叉树中的一个节点，该节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值，如果子节点的最大贡献值为正，则计入该节点的最大路径和，否则不计入该节点的最大路径和。维护一个全局变量 maxSum 存储最大路径和，在递归过程中更新 maxSum 的值，最后得到的 maxSum 的值即为二叉树中的最大路径和。



问题10：写题：找数组中第k大的数，复杂度
三种思路：一种是直接使用sorted函数进行排序，一种是使用小顶堆，一种是使用快排（双指针 + 分治）。
 
方法一：直接使用sorted函数进行排序
 
代码如下：


方法二：

维护一个size为 k 的小顶堆，把每个数丢进去，如果堆的 size > k，就把堆顶pop掉（因为它是最小的），这样可以保证堆顶元素一定是第 k 大的数。
 
代码如下：
时间复杂度：O(nlogk)
空间复杂度：O(k)
 
方法三：双指针 + 分治
 
partition部分
定义两个指针left 和 right，还要指定一个中心pivot（这里直接取最左边的元素为中心，即 nums[i]）

不断将两个指针向中间移动，使得大于pivot的元素都在pivot的右边，小于pivot的元素都在pivot的左边，注意最后满足时，left是和right相等的，因此需要将pivot赋给此时的left或right。

然后再将中心点的索引和 k - 1 进行比较，通过不断更新left和right找到最终的第 k 个位置。
 
代码如下：


时间复杂度：O(n)，原版快排是O(nlogn)，而这里只需要在一个分支递归，因此降为O(n)
空间复杂度：O(logn)