下一次国庆、中秋同一天要到哪一年？

先了解两个概念，回归年和朔望月。

• 回归年，又称为太阳年，指太阳连续两次通过春分点的时间间隔。

• 朔望月，是指月球连续两次合朔的时间间隔。但由于摄动，朔望月的长度有波动。

1 回归年 平均 = 365.2421990741 日 = 365 天 5 小时 48 分 46 秒。

1 朔望月 平均 = 29.530588 日 = 29 天 12 小时 44 分 2.8 秒（长度在 29.27 至 29.83 天之间变动）。

月有阴晴圆缺，人们习惯看月亮计日子，或者遥寄相思。但是一年有四季却是看太阳的脸色。总之，在制定历法时两者都得考虑进来。地球公转与月球公转相对地球自转来说，回归年和 12 个朔望月之间有差距，该怎么办呢？

经过简单计算可以发现， 19 个回归年的时间长度和 235 个朔望月几乎相同。所以阴阳历若采 19 年 7 闰法，即每 19 年加入 7 个闰月，就可以大致协调回归年（太阳的周期）与朔望月（月亮的周期）间的时间差距，以较为简易的方式制历。

在这种简单处理方式中，19 年中 12 年是 12 个阴历月，7 年是 13 个阴历月。可以将这 7 年放入一个六边形蜂窝阵列中，边上刚好 12 个围绕它们。

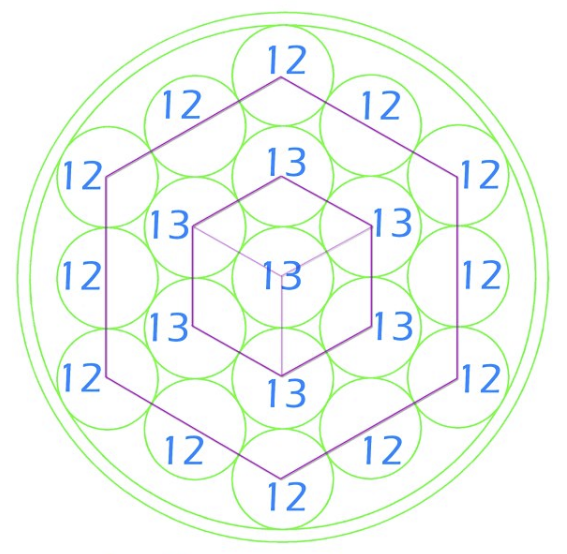
当然，全世界的各大文明都会遇到这个问题并想办法解决它。例如，默冬是古希腊天文学家，他在公元前 432 年的奥林匹克运动会上宣布他的发现: 即 19 个太阳年与 235 个朔望月的天数相等。因此阴历中，19 年置 7 个闰年就形成一个周期，在国外称为默冬周期。

另外，现在采用的公历是基于儒略历（Julian calendar）的。儒略历是由罗马共和国恺撒采纳数学家兼天文学家索西琴尼的计算后，于公元前 45 年 1 月 1 日起执行的取代旧罗马历法的一种历法。

儒略历中，一年被划分为 12 个月，大小月交替，四年一闰，平年 365 日，闰年 366 日为在当年二月底增加一闰日，年平均长度为 365.25 日。由于实际使用过程中的累积误差越来越大，1582 年教皇格里高利十三世颁布、推行了以儒略历为基础改善而来的格里历，即公历。

可见，即使只使用回归年，也还是有类似的问题。

好了，回到本文的主题，下一次国庆中秋双节同一天会是什么时候呢？我们先回顾下上两次确认一下，分别是 2001 年和 1982 年，相差十九年，完美。

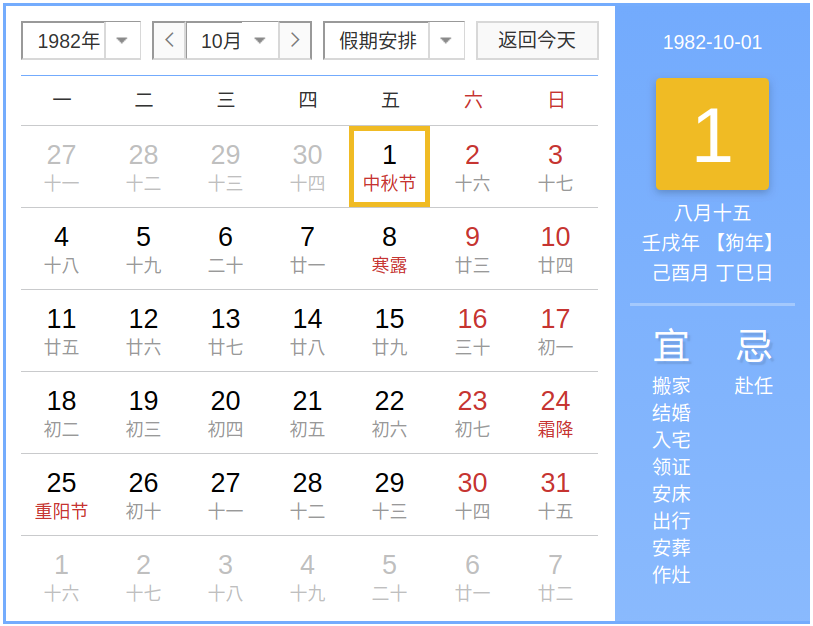
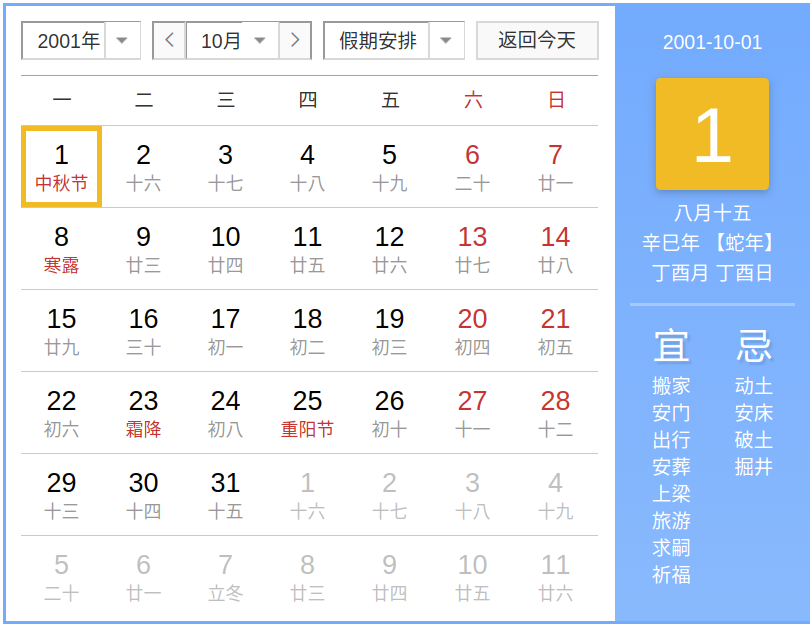
那么下一次会不会是 2039 年咯，结果一查，发现差了一天，

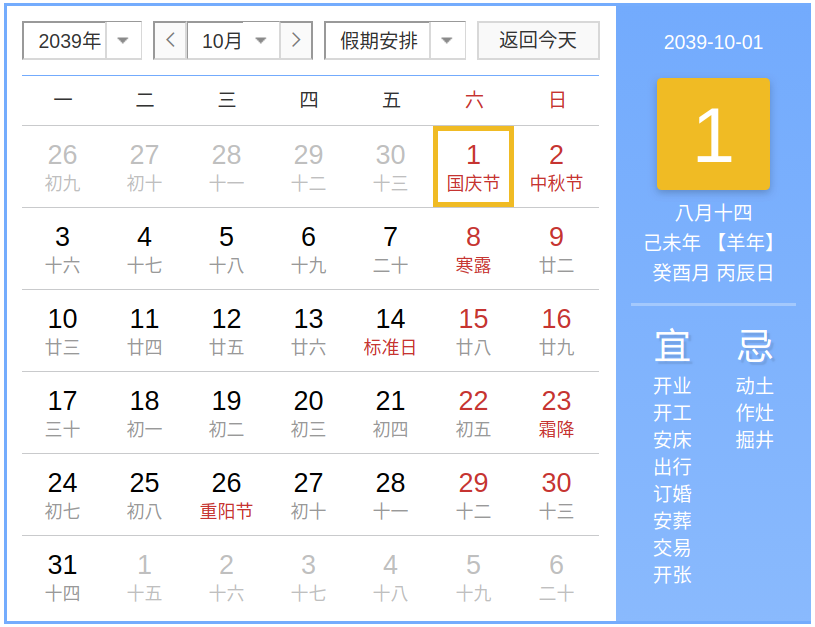
阴历跑快了一天，那就往前翻，发现提前到 2031 年了。

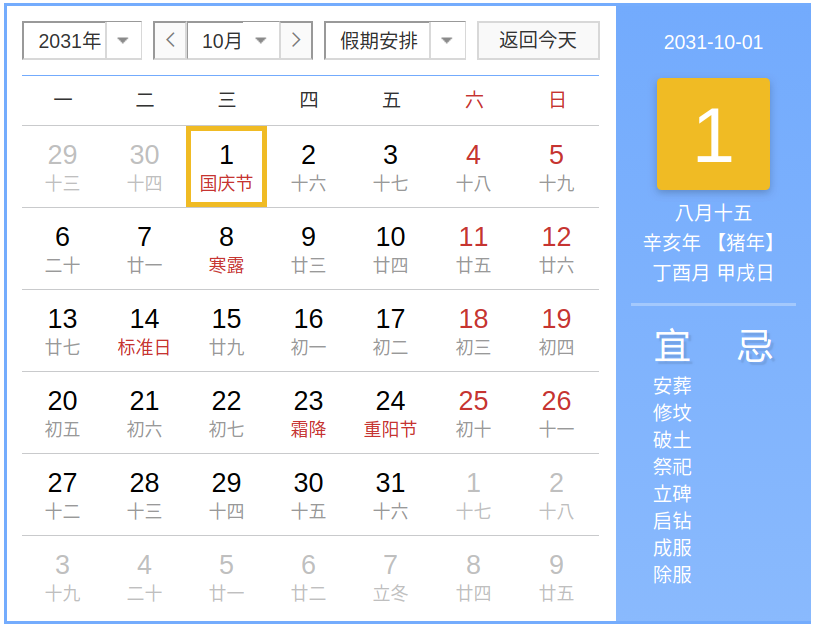
实际上 235 个朔望月约比 19 个回归年还是多了 1 h 27 m 33 s，所以仍然有一定误差。因此 19 年 7 闰也只是大概，还可以其他更精确的玩法。例如我国古代祖冲之（对，就是那个第一次将圆周率算到 3.1415926 和 3.1415927 之间的人）制定的《大明历》采用了更大的周期，在 391 年中插入 144 个闰月。他老人家那会儿算出的回归年是 天。

但实际上不管怎么个玩法，两个周期间始终有误差，19 年 7 闰法并不保证每过 19 年阴历和阳历就能精确循环了。因此，后期的平朔历法多会采取更精确而复杂的计算。

而本世纪最后一次双节重逢要到 2077 年了。希望各位保重身体，再次历经。