Python-数据特征分析-(统计量分析)

概要
用统计指标对定量数据进行统计描述，常从【集中趋势】和【离中趋势】两个方面进行分析。
平均水平的指标是对个体【集中趋势】的度量，使用最广泛的是均值和中位数；
反映变异程度的指标则是对个体【离开平均水平的度量】，使用较为广泛的指标是标准差（方差）、四分位间距。
1、集中趋势的度量
（1）均值：均值为所以数据的平均值。若计算n个观察数据的平均数，计算公式为：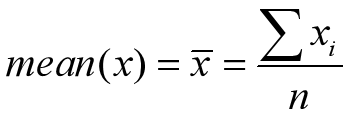

有时，为了反映在均值中不同成分的重要程度，为每个观察值 赋予 可以得到加权平均值：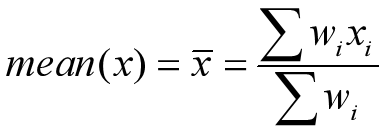

若每个数值出现概率为 ，则均值（期望）为：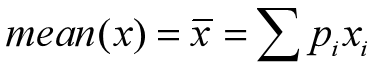

为了消除少数极端值的影响，可以使用截断均值或者中位数来度量数据的集中趋势。截断均值就是去除高低极端值之后的平均值。
（2）中位数：将所有数据值从小到大排好序，位于序列中间（位置）的那个数。即在全部数据中，小于和大于中位数的数据个数一样多
（3）众数：众数是数据集中出现最频繁的数值。众数并不经常用来度量定性变量的中心位置，更适合于定性变量。当然，众数一般用于离散型变量而非连续型变量。
2、离中趋势度量
（1）极差
极差=最大值-最小值
极差对数据集的极端值非常敏感，并且忽略了位于最大值于最小值直接的数据分布情况。
（2）标准差
标准差度量数据偏离均值的程度，计算公式为: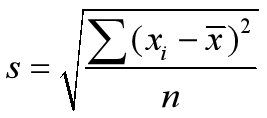

（3）变异系数
变异系数度量标准差相对于均值的离中趋势，主要用来比较两个或多个具有不同单位或者不同波动幅度的数据集的离中趋势。计算公式为：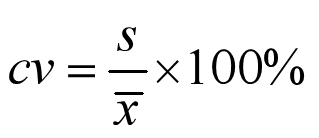

（4）四分位间距
四分位数包括上四分位数和下四分位数。将所有数值从小到大排序并分成四等份，处于第一个分割点位置的数值是上四分位数。
四分位数间距是上四分位数 与下四分位数 之差，其间包含了全部观察值的一半。其值越大，说明数据的变异程度越大；反之说明变异程度越小。

公众号推荐：数据思践

数据思践公众号记录和分享数据人思考和践行的内容与故事。

《数据科学与人工智能》公众号推荐朋友们学习和使用Python语言，需要加入Python语言群的，请扫码加我个人微信，备注【姓名-Python群】，我诚邀你入群，大家学习和分享。

关于Python语言，有任何问题或者想法，请留言或者加群讨论。