BN，Batch Normalization，就是在深度神经网络训练过程中使得每一层神经网络的输入保持相近的分布。

BN训练和测试时的参数是一样的吗？

对于BN，在训练时，是对每一批的训练数据进行归一化，也即用每一批数据的均值和方差。

而在测试时，比如进行一个样本的预测，就并没有batch的概念，因此，这个时候用的均值和方差是全量训练数据的均值和方差，这个可以通过移动平均法求得。

对于BN，当一个模型训练完成之后，它的所有参数都确定了，包括均值和方差，gamma和bata。

BN训练时为什么不用全量训练集的均值和方差呢？

因为在训练的第一个完整epoch过程中是无法得到输入层之外其他层全量训练集的均值和方差，只能在前向传播过程中获取已训练batch的均值和方差。那在一个完整epoch之后可以使用全量数据集的均值和方差嘛？

对于BN，是对每一批数据进行归一化到一个相同的分布，而每一批数据的均值和方差会有一定的差别，而不是用固定的值，这个差别实际上也能够增加模型的鲁棒性，也会在一定程度上减少过拟合。

但是一批数据和全量数据的均值和方差相差太多，又无法较好地代表训练集的分布，因此，BN一般要求将训练集完全打乱，并用一个较大的batch值，去缩小与全量数据的差别。

Dropout 是在训练过程中以一定的概率的使神经元失活，即输出为0，以提高模型的泛化能力，减少过拟合。

Dropout 在训练和测试时都需要吗？

Dropout 在训练时采用，是为了减少神经元对部分上层神经元的依赖，类似将多个不同网络结构的模型集成起来，减少过拟合的风险。

而在测试时，应该用整个训练好的模型，因此不需要dropout。

Dropout 如何平衡训练和测试时的差异呢？

Dropout ，在训练时以一定的概率使神经元失活，实际上就是让对应神经元的输出为0

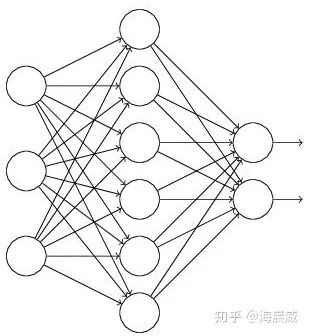
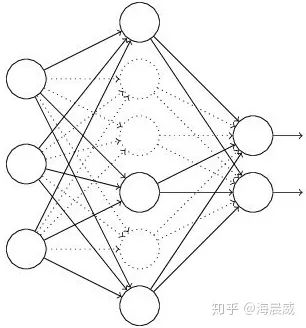
假设失活概率为 p ，就是这一层中的每个神经元都有p的概率失活，如下图的三层网络结构中，如果失活概率为0.5，则平均每一次训练有3个神经元失活，所以输出层每个神经元只有3个输入，而实际测试时是不会有dropout的，输出层每个神经元都有6个输入，这样在训练和测试时，输出层每个神经元的输入和的期望会有量级上的差异。

因此在训练时还要对第二层的输出数据除以（1-p）之后再传给输出层神经元，作为神经元失活的补偿，以使得在训练时和测试时每一层输入有大致相同的期望。

dropout部分参考：

https://blog.csdn.net/program_developer/article/details/80737724

BN和Dropout共同使用时会出现的问题

BN和Dropout单独使用都能减少过拟合并加速训练速度，但如果一起使用的话并不会产生1+1>2的效果，相反可能会得到比单独使用更差的效果。

相关的研究参考论文：

Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift

https://arxiv.org/abs/1801.05134

本论文作者发现理解 Dropout 与 BN 之间冲突的关键是网络状态切换过程中存在神经方差的（neural variance）不一致行为。试想若有图一中的神经响应 X，当网络从训练转为测试时，Dropout 可以通过其随机失活保留率（即 p）来缩放响应，并在学习中改变神经元的方差，而 BN 仍然维持 X 的统计滑动方差。这种方差不匹配可能导致数值不稳定（见下图中的红色曲线）。而随着网络越来越深，最终预测的数值偏差可能会累计，从而降低系统的性能。简单起见，作者们将这一现象命名为「方差偏移」。事实上，如果没有 Dropout，那么实际前馈中的神经元方差将与 BN 所累计的滑动方差非常接近（见下图中的蓝色曲线），这也保证了其较高的测试准确率。

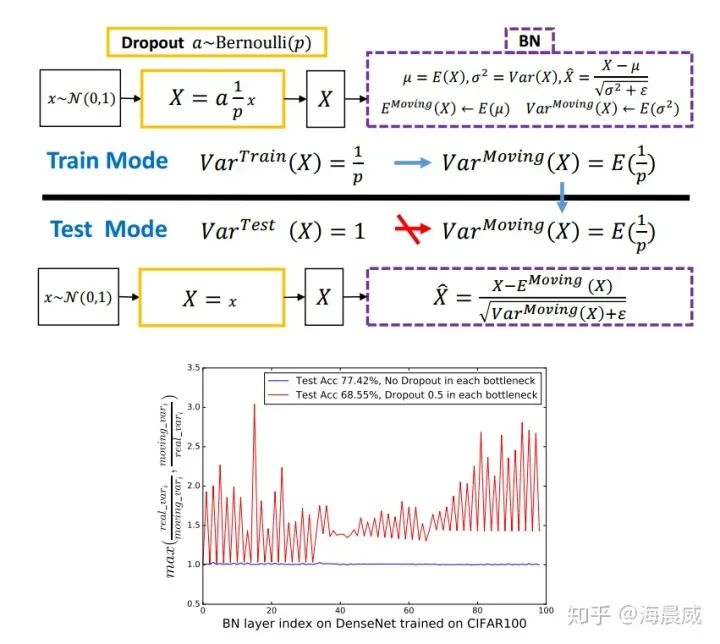
作者采用了两种策略来探索如何打破这种局限。一个是在所有 BN 层后使用 Dropout，另一个就是修改 Dropout 的公式让它对方差并不那么敏感，就是高斯Dropout。

第一个方案比较简单，把Dropout放在所有BN层的后面就可以了，这样就不会产生方差偏移的问题，但实则有逃避问题的感觉。

第二个方案来自Dropout原文里提到的一种高斯Dropout，是对Dropout形式的一种拓展。作者进一步拓展了高斯Dropout，提出了一个均匀分布Dropout，这样做带来了一个好处就是这个形式的Dropout（又称为“Uout”）对方差的偏移的敏感度降低了，总得来说就是整体方差偏地没有那么厉害了。

该部分参考：

https://www.jiqizhixin.com/articles/2018-01-23-4

https://zhuanlan.zhihu.com/p/33101420