5种解法的算法面试题 来看看你是青铜还是王者?
作者:xindoo
来源:SegmentFault 思否社区
先来详细描述下这道题。在一个全为正整数的数组中找到总和为给定值的子数组,给出子数组的起始下标(闭区间),举个例子:
在[3 2 1 2 3 4 5]这个数组中,和为10的子数组是[1 2 3 4],所以答案应该是[2,5]。
和为15的子数组是[1 2 3 4 5],答案为[2,6]。
这是一道非常有意思的题,为什么这么说?最简单的解法只要具备基本的编程知识就能写出,更优的解法需要你有数据结构和算法能力,越高效的解法越巧妙,可能你一下子无法想出所有的解法,但我相信你看完这篇博客一定会感叹算法的神奇。
回到这道题上来,实际上它有着O(n^3) 、O(n^2) 、O(nlogn) 、O(n) 4种时间复杂度的解法,如果算上空间复杂度的差异的话总共5种解法,我觉得还是比较能考察到一个人的算法水平的。接下来让我带领大家由简入难看下从青铜到王者的5种解法,带大家吊打面试官。
这里我们设输入参数为(arr[],target),后续代码中我会用s和e来分别表示起始和终止位置。另外为了简化代码思路,我们假设给定的参数里最多只有一个解(实际上多个解也不难,但会让代码变长,不利于描述思路,多解的情况就留给你当课后作业了)。
青铜-暴力求解
首先当然是最简单的暴力求解了,遍历起始位置s和结束位置e,然后求s和e之间所有数字的和。三层循环简单粗暴,不需要任何的技巧,相信你大一刚学会编程就能解出来。
public int[] find(int[] arr, int target) {
for (int s = 0; s < arr.length; s++) {
for (int e = s+1; e < arr.length; e++) {
int sum = 0;
for (int k = s; k <= e; k++) { // 求s到e之间的和
sum += arr[k];
}
if (target == sum) {
return new int[]{s, e};
}
}
}
return null;
}
我们来分析下时间复杂度,很明显是O(n^3),当n超过1000时就会出现肉眼可见的慢,想想如何优化?
白银-空间换时间
上面代码中,我们每次都需要算从s到e之间的数组的和sum[s,e],假设我之前已经求过了[1,10]之间的和sum[1,10],现在要求[2,10]之间的和sum[2,10],显然这中间有很大一部分是重叠的(sum[2,10]),能不能把这部分重复扫描给消除掉?这里就需要做下巧妙的变换了。
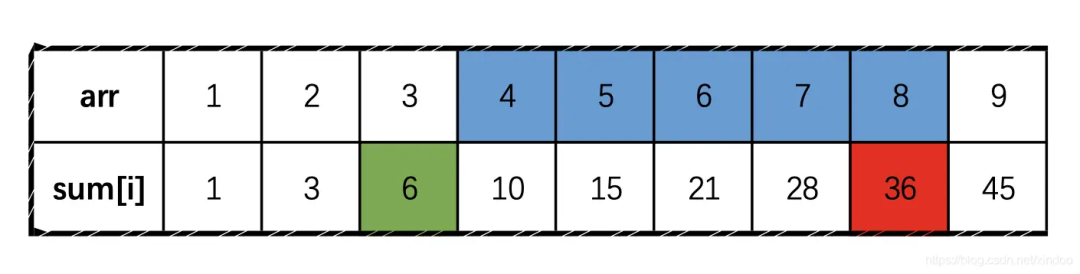
sum[s, e] = sum[0, e] - sum[0, s-1], sum[0,i]我们可以预先保存下来,然后重复使用。实际上sum数组我们可以通过一遍数据预处理获取到。上图中,arr蓝色区域的和正好等于sum数组中红色减去绿色,即sum(arr[3]-arr[7]) = sum[7]-sum[2]。 public int[] find(int[] arr, int target) {
int[] sumArr = new int[arr.length + 1];
for (int i = 1; i < sumArr.length; i++) {
sumArr[i] = sumArr[i-1] + arr[i-1]; // 预处理,获取累计数组
}
for (int s = 0; s < arr.length; s++) {
for (int e = s+1; e < arr.length; e++) {
if (target == sumArr[e+1] - sumArr[s]) {
return new int[]{s, e};
}
}
}
return null;
}
O(n^3) 降低到O(n^2)。黄金-二分查找
public int[] find(int[] arr, int target) {
int[] sumArr = new int[arr.length + 1];
for (int i = 1; i < sumArr.length; i++) {
sumArr[i] = sumArr[i-1] + arr[i-1];
}
for (int s = 0; s < arr.length; s++) {
int e = bSearch(sumArr, sumArr[s] + target);
if (e != -1) {
return new int[]{s, e};
}
}
return null;
}
// 二分查找
int bSearch(int[] arr, int target) {
int l = 1, r = arr.length-1;
while (l < r) {
int mid = (l + r) >> 1;
if (arr[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
if (arr[l] != target) {
return -1;
}
return l - 1;
}
钻石-HashMap优化
public int[] find(int[] arr, int target) {
int[] sumArr = new int[arr.length + 1];
Map<Integer, Integer> map = new HashMap<>();
for (int i = 1; i < sumArr.length; i++) {
sumArr[i] = sumArr[i-1] + arr[i-1];
map.put(sumArr[i], i-1);
}
for (int s = 0; s < arr.length; s++) {
int e = map.getOrDefault(sumArr[s]+target, -1);
if (e != -1) {
return new int[]{s, e};
}
}
return null;
}
王者-尺取法

public int[] find(int[] arr, int target) {
int s = 0, e = 0;
int sum = arr[0];
while (e < arr.length) {
if (sum > target) {
sum -= arr[s++];
} else if (sum < target) {
sum += arr[++e];
} else {
return new int[]{s, e};
}
}
return null;
}
总结

评论
