Python与Tableau相结合,万字长文搞定传统线下连锁店数据分析


来源:凹凸数据
1 分析背景:
这是kaggle上的一份巴西传统线下汽车服务类连锁店的实际销售数据,大小约3.43G,包含了从2017年3月31日到2020年4月1日大约2600万多的销售数据。
分析该数据集可以探究该连锁店的销售情况,产品的分布,可以对客户进行细分,精细化销售,对员工的生产力进行分析。
这里是利用Python结合Tableau来进行分析,可视化用的Tableau,部分分析用的Python。
数据解读:
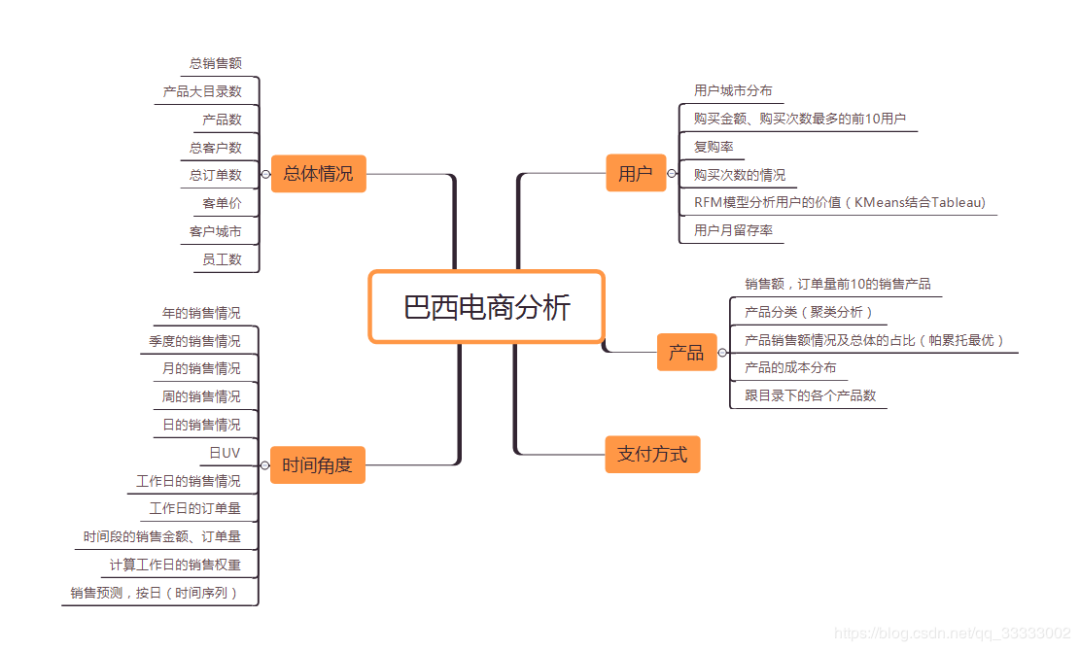
2 分析框架
3 数据清洗
3.1 读取数据,看看总体情况
这里的数据集比较大,Anaconda加载的数据都暂时存在内存里,笔者刚开始用的8G内存,一下子就满了,这里建议8-12G的内存左右,或者关闭一些暂时不用先的软件。
# 导入相关包
import numpy as np
import pandas as pd
# 读取数据,设置分割符号
file_path = r'F:\ales Report.csv\Sales Report.csv'
df = pd.read_csv(file_path, iterator=True, sep=';')
data = df.get_chunk(30000000)
data.info()
输出:
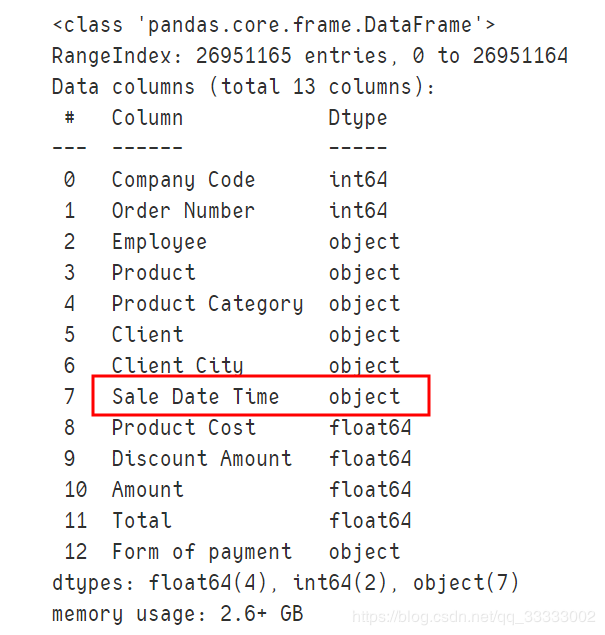
这里的销售时间是object类型,要转换成datetime类型,先记录下。
# 查看NULL的数据:
data.isnull().sum()
输出:
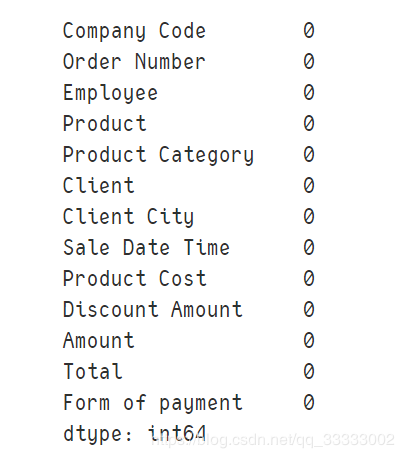
这里的数据比较干净,都没有NULL值这些。
查看数据的标准差,最大,最下值这些:
data.describe()
输出:
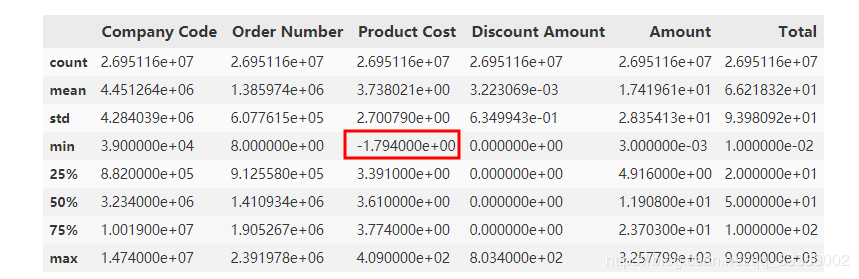
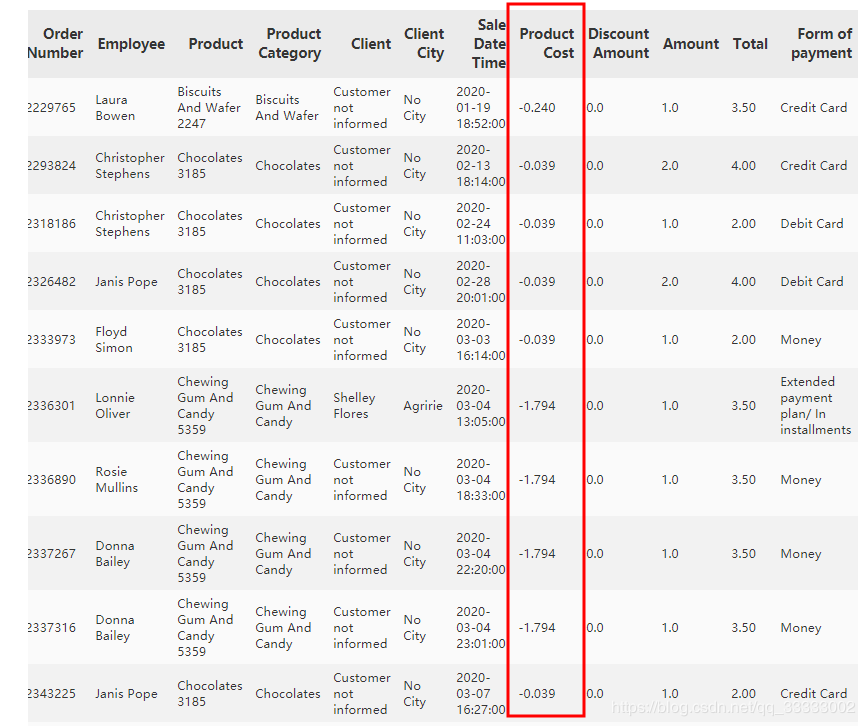
这里的数据量比较多,数据相对比较大,这里很明显可以看出的Product Cost这里有个负数,查看这些数据:
data[data['Product Cost'] <= 0]
输出:
len(data[data['Product Cost'] < 0])
输出:
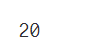
这里按照字面的意思理解是每销售出一个该产品的成本,这里为负数,暂且这里当异常数据去处理,这里的数据量也不多,只有20条,直接删除处理。实际,得和业务进行沟通,查看该指标的具体意思,和该负数情况的发生是出于什么情况来进行分析。
删除这些数据:
data.drop(index=data[data['Product Cost'] < 0].index, inplace=True)
3.2 删除重复的数据
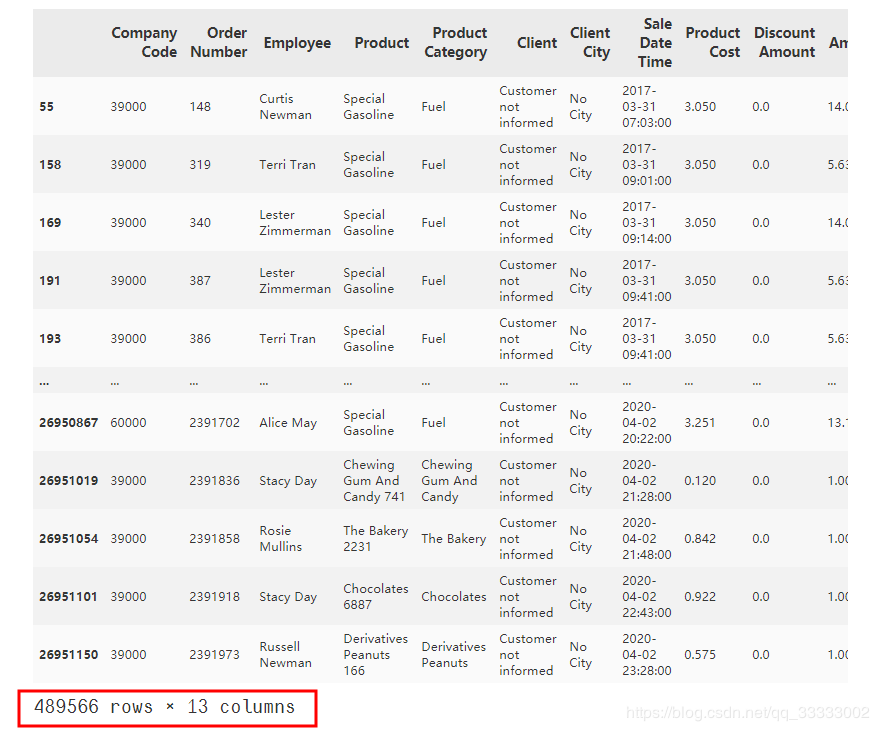
# 数据清洗,这里有489567条数据是重复的,删除这些数据
data[data.duplicated()]
输出:
# 删除重复的数据
# 这里的重复的数据是完全重复的,所有的值都是相同的,
# 这里只能判断为异常数据,直接删除掉
data.drop(index=data[data.duplicated()].index, inplace=True)
3.3 日期转换格式
data['Sale Date Time'] = pd.to_datetime(data['Sale Date Time'])
data.info()
输出:
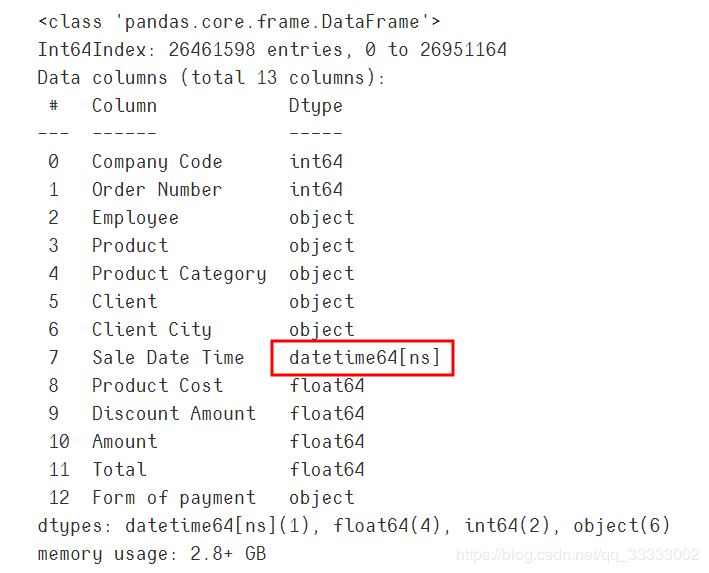
至此,数据清洗完毕,可以进行分析。
4 分析
4.1 总体情况
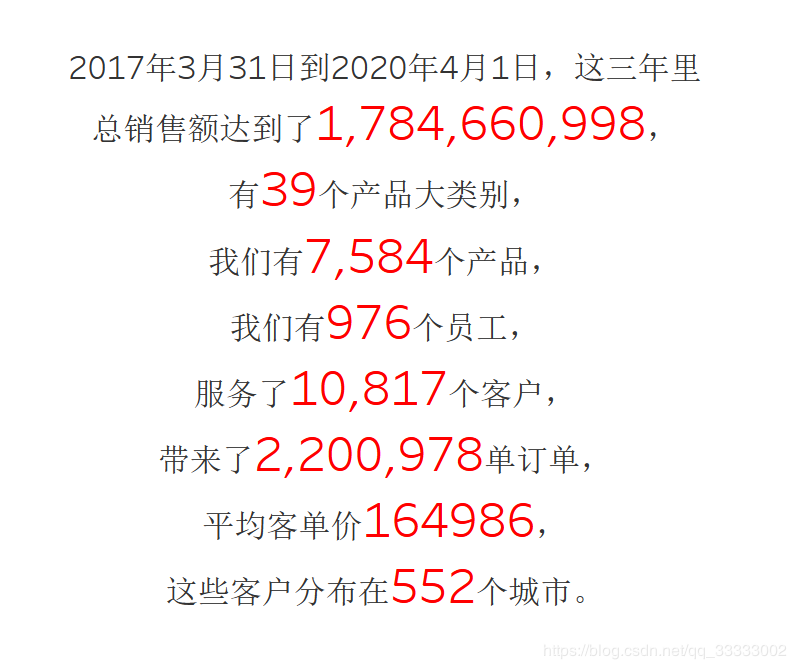
4.2 时间角度
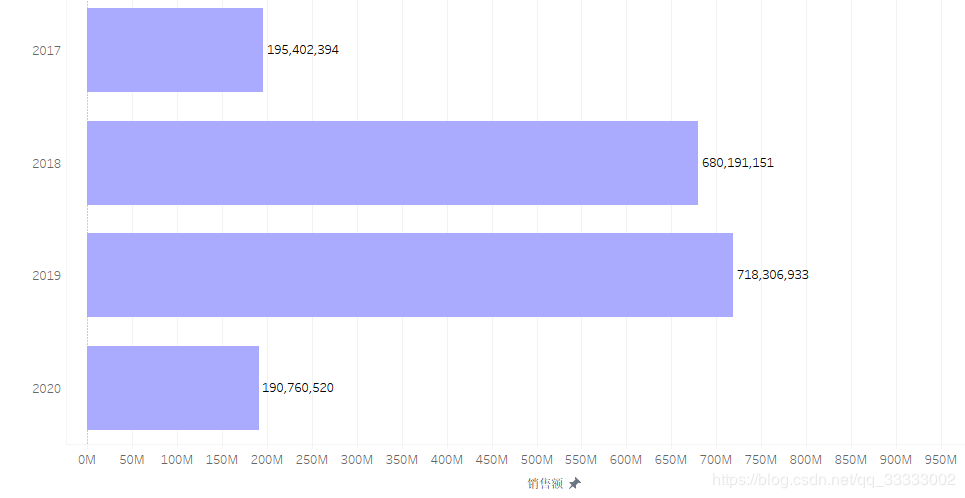
4.2.1 年销售额情况
2017年只有前9个月的销售额,2020年只有前4个月的销售额。
2019年总销售额达到718306933,环比2018年的680191151,增长5.6%。
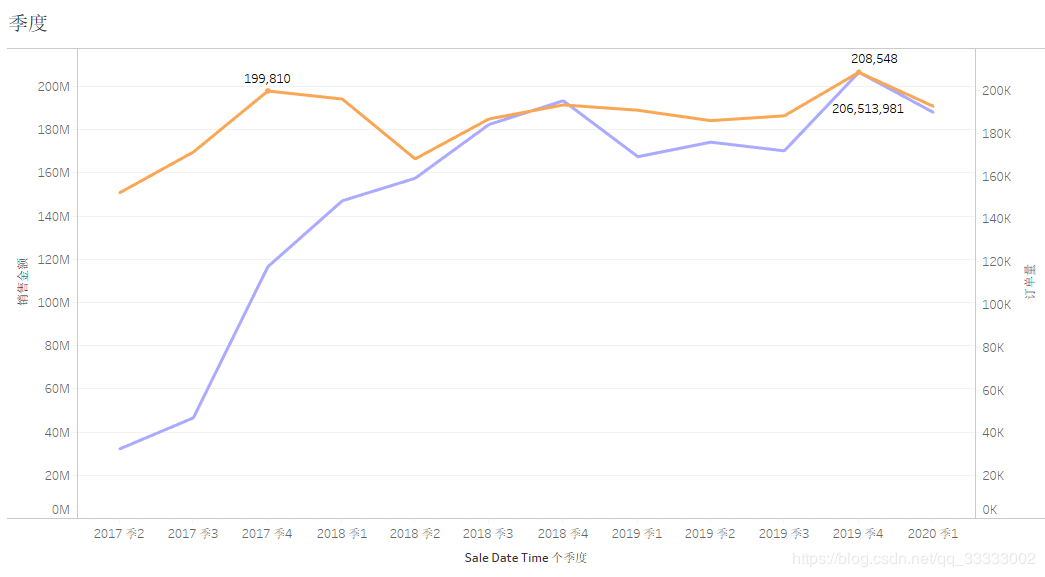
4.2.2 季度的销售额情况
2017第二季度开始到2018年底订单量成直线式上涨,2019年较平稳。
2017年该连锁店出于疯狂生长期,订单量、销售额均呈现直线上升趋势。
2019年第四季度订单量:208548,销售额达到206513981,订单量、销售金额均达到历史峰值。
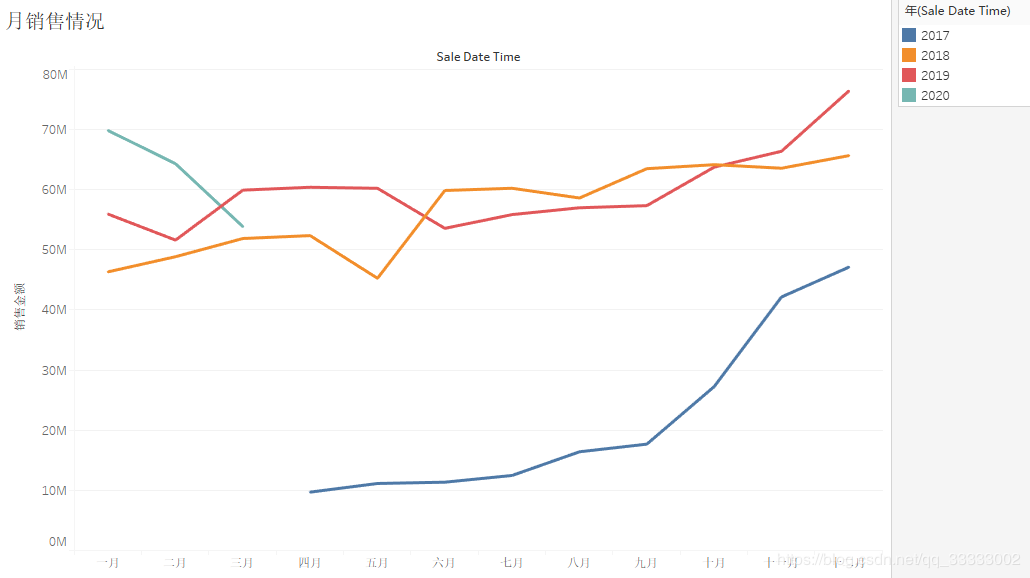
4.2.3 月的销售情况
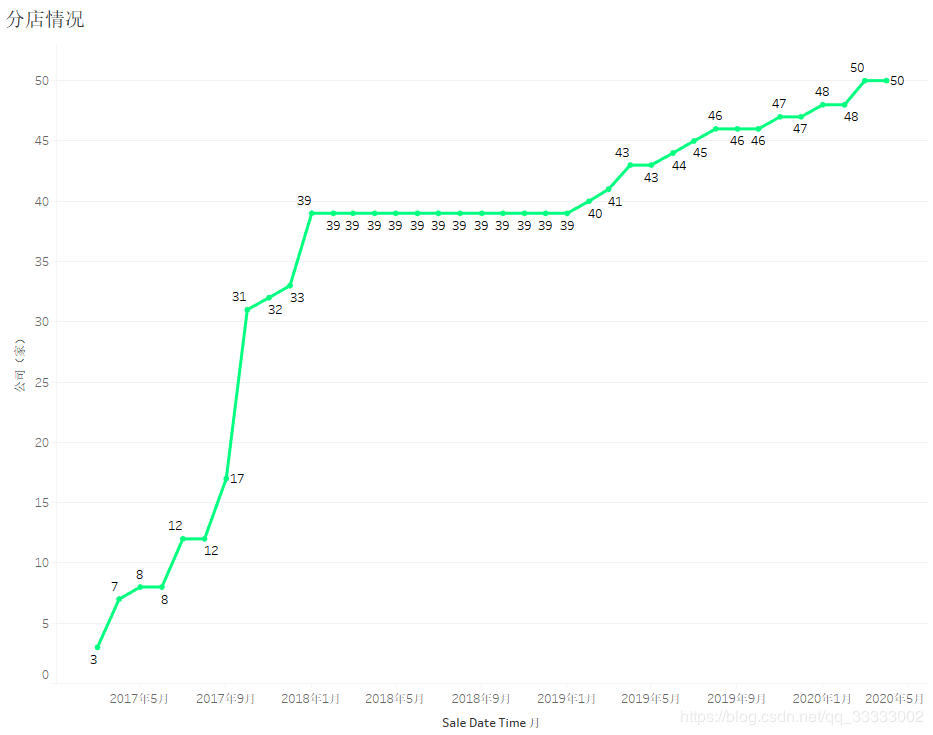
2017年各月份的销售金额,呈上涨趋势,其中17年下半年上涨趋势较明显,18、19年呈现较稳定的状态;结合各月份,连锁店的数量。
可以得出结论:2017年下半年连锁店数量的增加带动销售金额明显的上涨。
结合2018、2019年对比,该连锁店的销售额不受季节的影响,12月为了冲业绩,销售额会上涨一些。
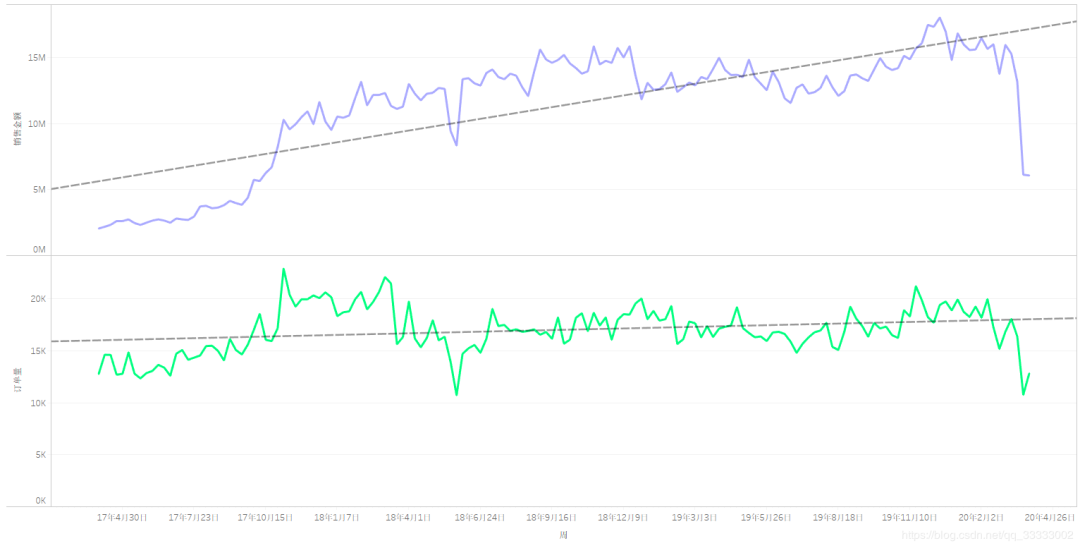
4.2.4 周的销售情况
周的销售金额总体上先呈现上升,然后趋向于较稳定的状态。
周的订单量处于动态的平衡当中,可以看出随着时间的增长,每张订单的购买金额逐渐增加。
4.2.5 日的销售情况
总体来说,这里只有2018年6月1日左右时间段的销售金额有异常,这段时间既有极大值,也有极小值。具体原因可以深入查明一下。
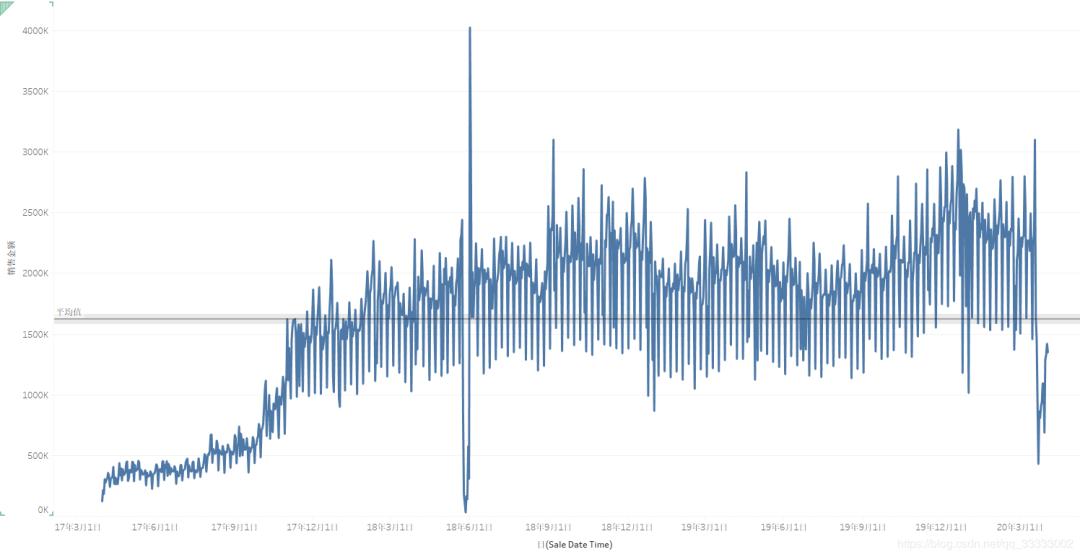
这里的日销售额呈现周期性规律,也就是有6天销售额处于较高的,有一天的销售额是处于最低的,结合工作日权重,可以看出,巴西人民再周日的购买欲望较低,或者该商圈处于写字楼附近。
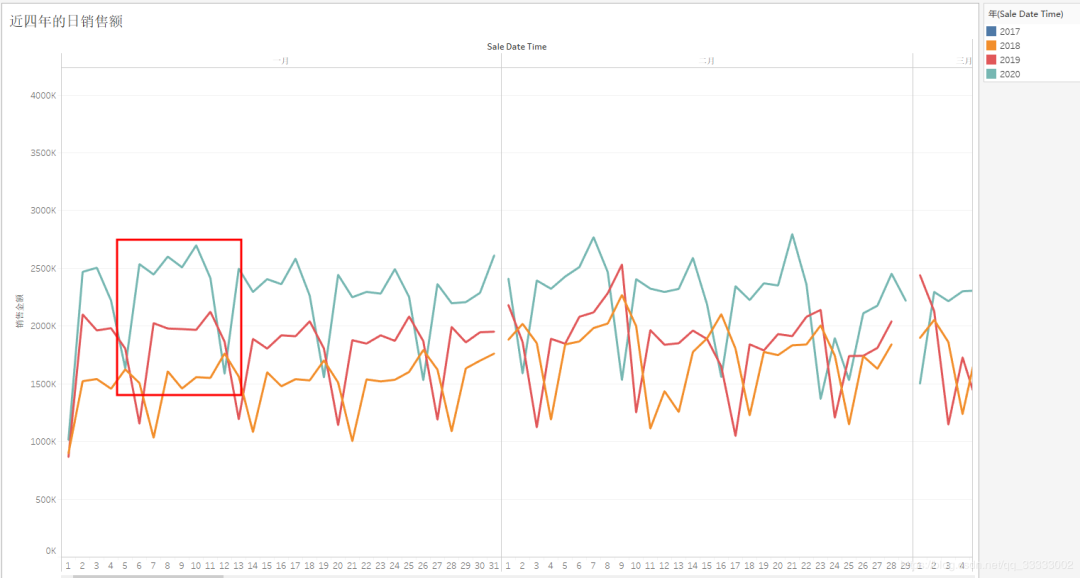
4.2.6 近四年的日UV
纵向对比每年的日UV,都有上升的趋势。
横向对比当年的日UV,呈现周期性的规律,这里按7天为一周期,前后一天都是最低的,中间五天相对来说较高。
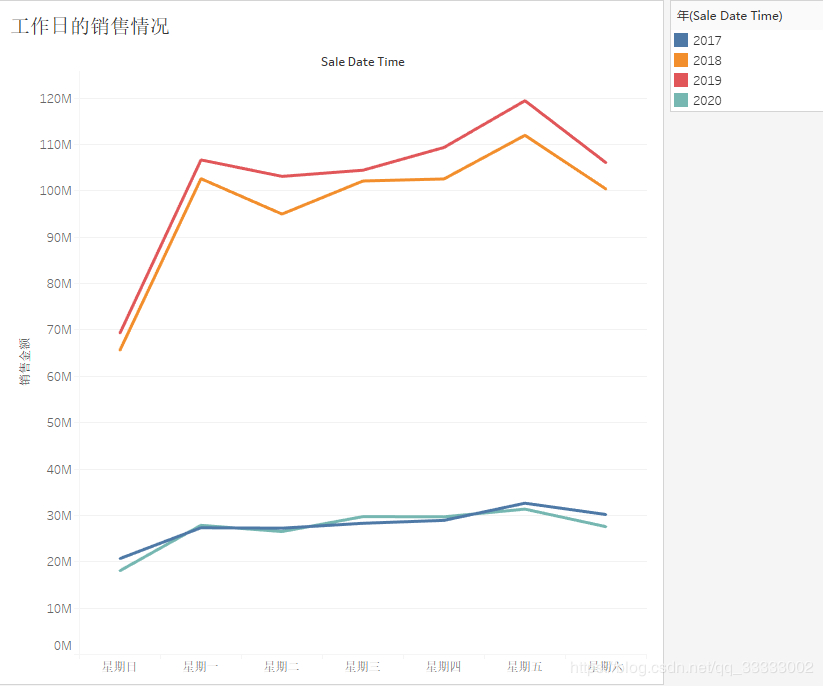
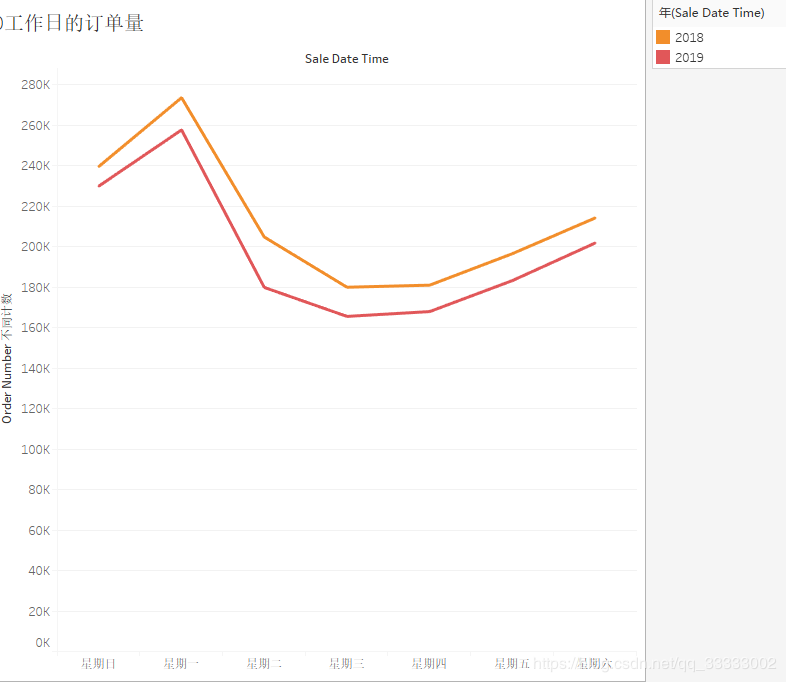
4.2.7 工作日的销售情况
周日的销售金额最少。
4.2.7 工作日的订单量
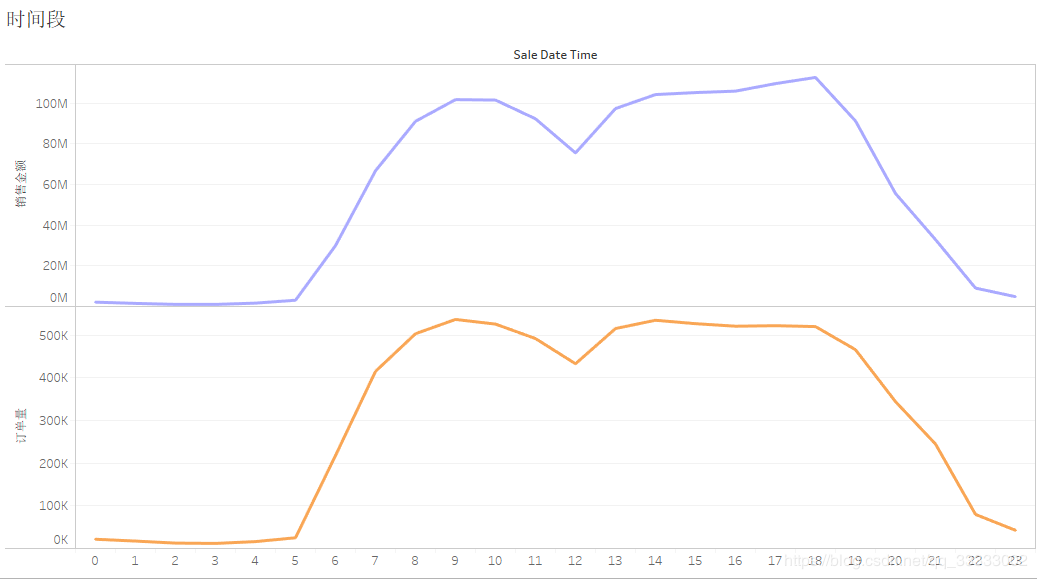
4.2.8 时间段的销售金额、订单量
该商城销售额、订单量在7-20点这个时间段较高,12点有个谷底。
4.2.9 工作日的销售权重
这里只挑选了2019年全年的数据来进行统计。
在Tableau里实现: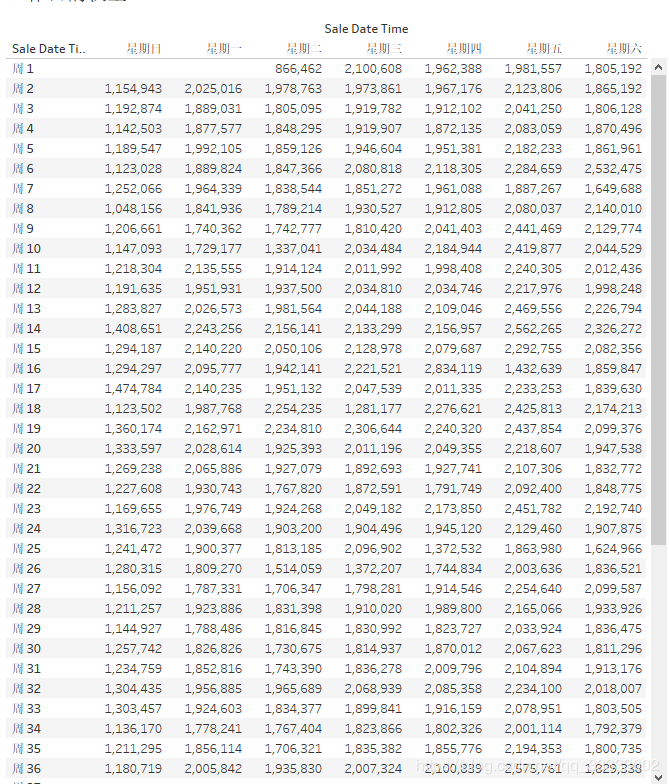
导出数据到Excel里计算。
计算公式方式:
全年周日的平均值=全年的周日的总销售额/全年周日的天数,其他工作日类推。 挑选1中计算到的最小值 权重=某个工作日的平均值 / 2中选出的最小值
这里的权重越大,表明当日的销售额越多。

可视化:
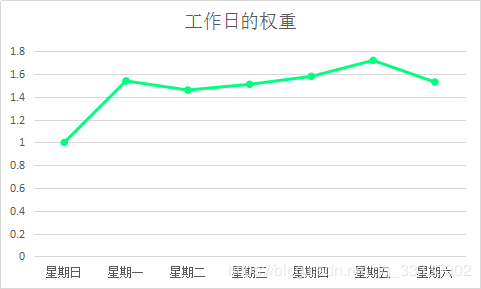
这里可得出的结论:周五的销售权重最大,周日的销售权重最小。
4.2.10 销售预测按日
这里只挑选2019年1月1日到2020年2月29的数据,其中2020年2月份的数据用来做预测和对比。
# 将销售时间设置成索引
data.set_index('Sale Date Time', inplace=True, drop=True)
# 将数据重新整理成以天来统计每天销售额的汇总
day_data = data.resample('d').sum()['Total']
day_data
输出:
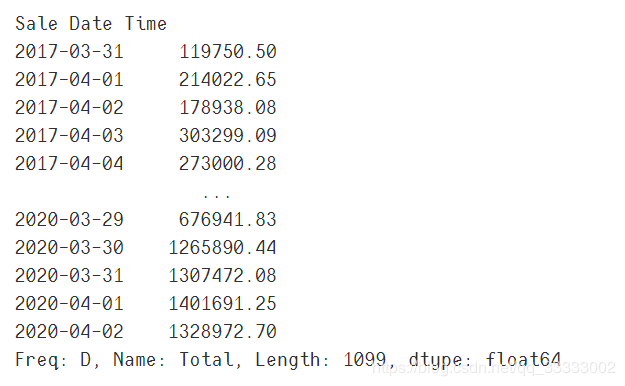
# 挑选2019年1月1日到2020年2月29的数据
train_day_data = day_data[day_data.index >= '2019-01-01']
train_day_data = train_day_data[train_day_data.index <= '2020-02-29']
# 保存数据到Excel
train_day_data.to_excel('./日销售数据.xlsx')
# 读取数据
data = pd.read_excel('./日销售数据.xlsx')
# 重新命名列
data.rename(columns={'Sale Date Time': 'date1'}, inplace=True)
data
输出:
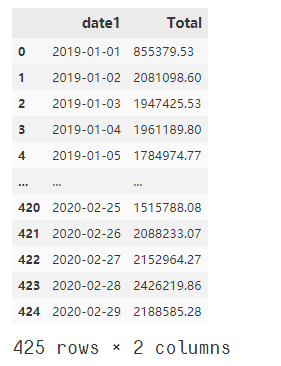
# 将销售额进行缩放,预测的只是大概的值,不可能太精确,这里直接根据数据的情况,以10万作为基本的单位。
data['Total'] = round(data['Total'] / 100000, 4)
进行平稳性检验
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
%matplotlib inline
# 时序图
plt.figure(figsize=(18, 8), dpi=256)
data['Total'][:-30].plot()
输出:
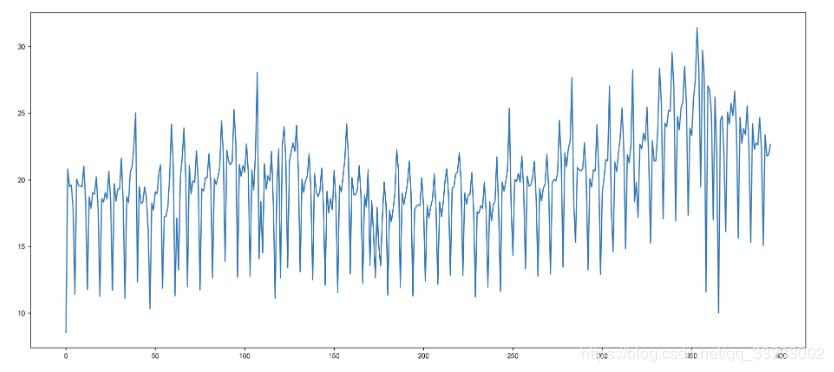
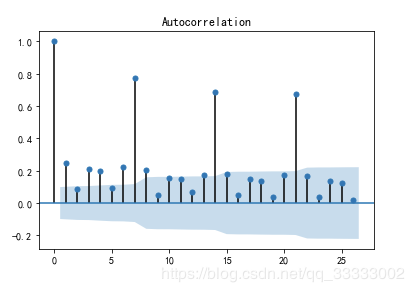
# 自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data['Total'][:-30])
plt.figure(figsize=(18, 8), dpi=256)
输出:
# 偏自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(data['Total'][:-30])
plt.figure(figsize=(18, 8), dpi=256)
输出:
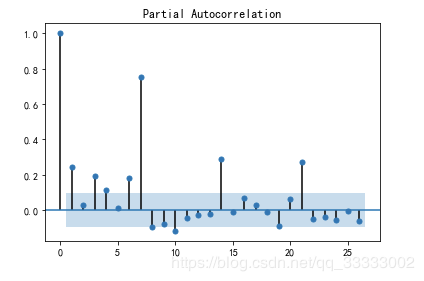
# 单位跟检验
from statsmodels.tsa.stattools import adfuller as ADF
print(ADF(data['Total'][:-30]))
输出:
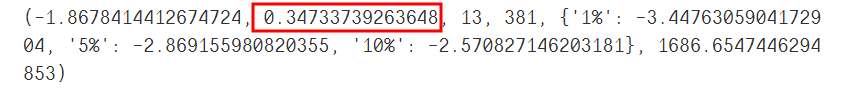
这里的p值等于0.347多,大于0.05,属于不平稳序列,需要进行差分后,再检验是否属于平稳序列。
# 一阶差分
D_data = data['Total'][:-30].diff().dropna()
print('一阶段差分检验结果:', ADF(D_data))
输出:

一阶差分后的序列,属于平稳序列,这里可以使用差分后平稳序列的模型ARIMA进行预测,预测前还得进行白噪声检验。
from statsmodels.stats.diagnostic import acorr_ljungbox
print('白噪声检验结果:', acorr_ljungbox(D_data, lags=1))
输出:
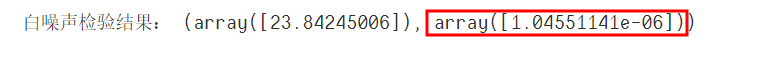
白噪声检验的p值远小于0.05,一阶差分后的时间序列属于平稳非白噪声的时间序列,下面可以利用ARIMA模型进行预测。
from statsmodels.tsa.arima_model import ARIMA
from datetime import datetime
from itertools import product
# 设置p阶,q阶范围
# product p,q的所有组合
# 设置最好的aic为无穷大
# 对范围内的p,q阶进行模型训练,得到最优模型
ps = range(0, 5)
qs = range(0, 5)
parameters = product(ps, qs)
parameters_list = list(parameters)
best_aic = float('inf')
results = []
for param in parameters_list:
try:
model = ARIMA(data['Total'][:-30], order=(param[0], 1, param[1])).fit()
except ValueError:
print("参数错误:", param)
continue
aic = model.aic
if aic < best_aic:
best_model = model
best_aic = model.aic
best_param = param
results.append([param, model.aic])
results_table = pd.DataFrame(results)
results_table.columns = ['parameters', 'aic']
print("最优模型", best_model.summary())
输出:
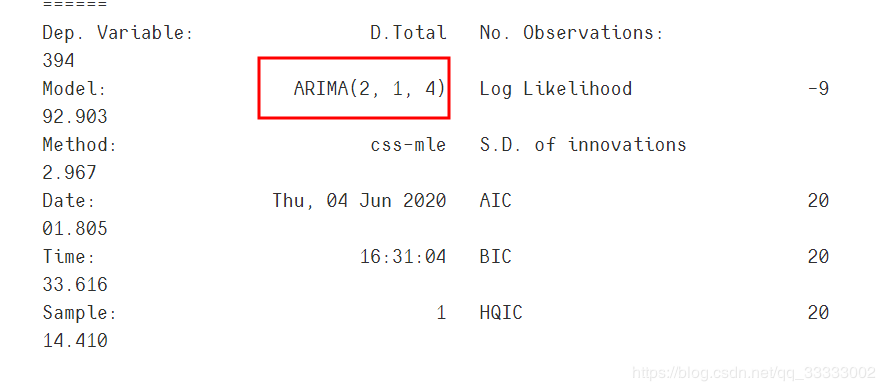
利用最好的模型进行预测。
best_model.forecast(30)[0]

模型评价:
from sklearn.metrics import mean_absolute_error
# pred_y 预测值
# test_y 实际值
pred_y = best_model.forecast(30)[0]
test_y = data['Total'][-30:].values
mean_absolute_error(test_y, pred_y)
输出:
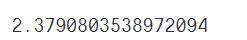
这里的平均绝对误差为2.38,这里要根据实际的业务确定误差阈值。再来进行模型的评价。小于阈值的,模型就是稍微好的,大于阈值的,说明模型的准确率还有待提高,模型还需重新训练等。
画折线图,对比下实际和预测值之间的差距。
plt.figure(figsize=(14, 7), dpi=256)
plt.plot(data['date1'][-30:], test_y, label='实际')
plt.plot(data['date1'][-30:], pred_y, label='预测')
plt.xticks(data['date1'][-30:], rotation=70)
plt.legend(loc=3)
输出:
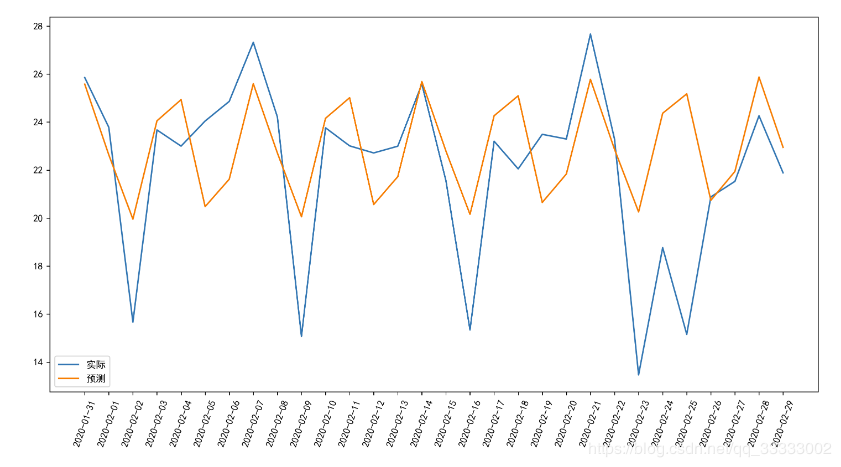
这里可以看出,模型预测的结果还是稍微好点的。
4.3 用户角度
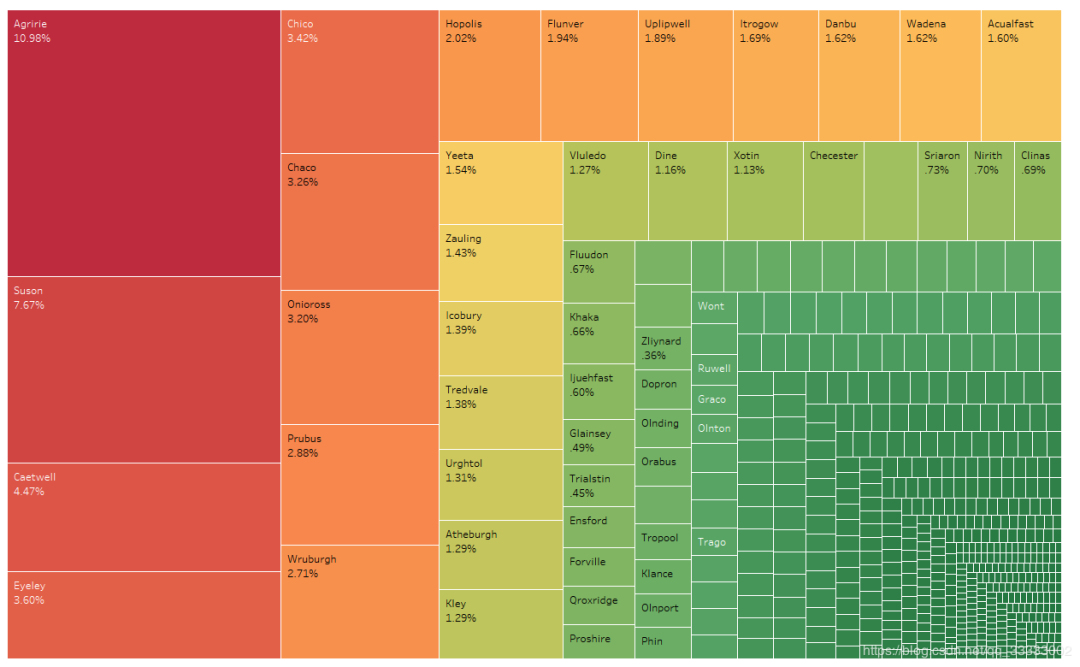
4.3.1 用户城市分布
10.98%的用户集中在Agirrie这个城市,用户居住城市相对较分散。
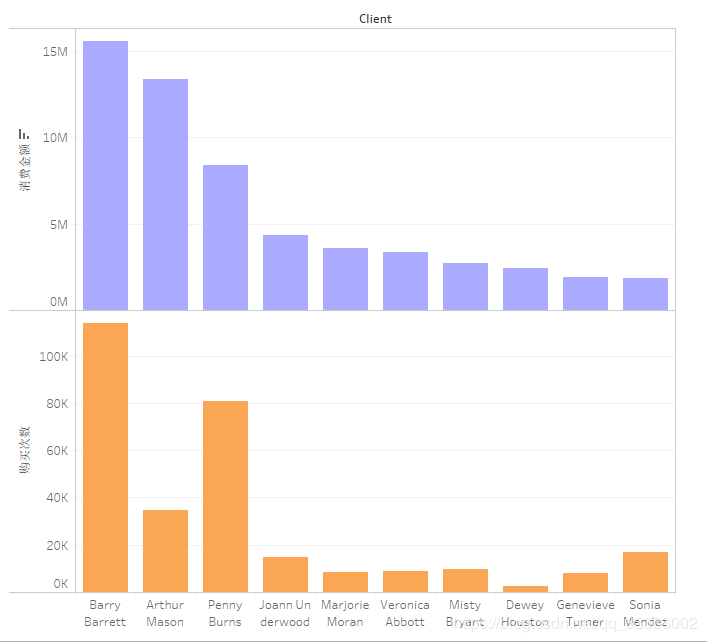
4.3.2 用户购买金额,购买次数前10的用户
用户Barry Barrett总购买金额达到15M以上,消费次数也达到了100K以上,属于高价值的客户。
4.3.3 复购率
总体复购率:
这里是按这份数据所在的时间段,计算购买次数大于2次的用户,再除于总的用户数,这里得排除的一个数据是用户Client这里,有一个数据是Customer not informed(客户没有提供名字的情况),这条数据得排除了,所以计算购买次数大于2的用户和总用户数对应减去1,这是个人的想法,实际是得和业务沟通,得到实际的计算方法。查看Customer not informed这条数据:
# 计算每个客户的购买次数,这里使用了nunique(),统计不同订单号的个数
client_data = data.groupby('Client').nunique()['Order Number']
# 重命名列
client_data = client_data.reset_index().rename(columns={'Order Number':
'user_num'})
client_data.sort_values('user_num', ascending=False)

# 总复购率
print('总复购率:',
round(
(len(client_data[client_data['user_num'] > 1])-1) /
(len(client_data) - 1), 4) * 100, "%")
输出:
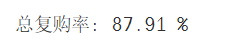
该数据所在的时间段的总体复购率达到了87.91%,用户黏性较高。
这里再细分下,看下一个月内的复购的情况。
一个月内复购率
这里的一个月内复购率的定义是:从月初的1号到月底这段时间内,用户复购的比率。
# 这里的销售时间是datetime格式,增加个辅助列,转换成2017-01这样的年月显示
def parse_year_month(x):
if x.month >= 10:
return str(x.year) + "-" + str(x.month)
else:
return str(x.year) + "-0" + str(x.month)
data['year_month'] = data['Sale Date Time'].apply(parse_year_month)
统计每个月用户的购买次数
y_m_data = data.groupby(['year_month',
'Client']).nunique()['Order Number'].reset_index()
y_m_data
输出:
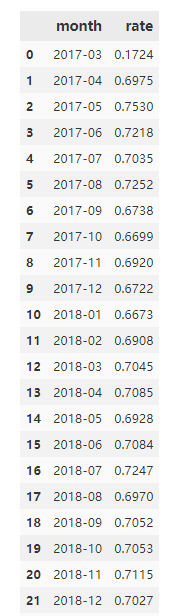
每个月的复购率
# 保存临时数据,用于构建每月的复购率的DataFrame
month_list = []
rate_list = []
# 循环计算每个月的复购率,这里直接遍历每个月
for every_m in y_m_data['year_month'].unique():
# 获取每个月用户的购买次数的数据
temp = y_m_data[y_m_data['year_month'] == every_m]
# print(every_m, "复购率:",
# round((len(temp[temp['Order Number'] > 1])-1) / (len(temp) -1),4))
month_list.append(every_m)
# 选出购买次数>1的数据,获取数据的长度(用户数)- 1 再除以
# 当月的总用户数 -1
rate_list.append(round((len(temp[temp['Order Number'] > 1])-1) / (len(temp) -1), 4))
#将数据转换成DataFrame
t_1 = {'month': month_list, 'rate': rate_list}
rate_data = pd.DataFrame(t_1)
rate_data
输出:
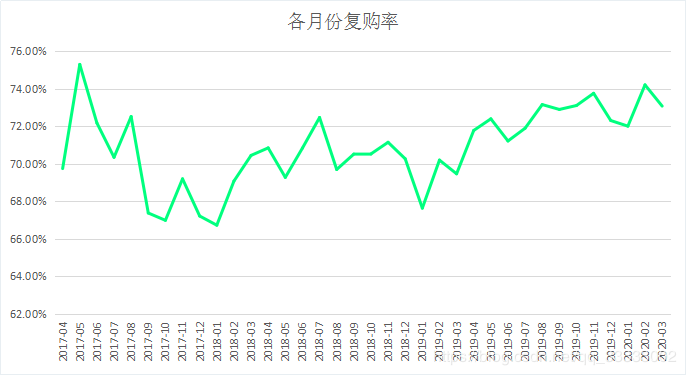
导出数据,用Excel做可视化:
rate_data.to_excel('./rate_data.xlsx', index=False)
月复购率都在66%以上,用户的黏性较大。
4.3.4 购买次数的情况
这里只挑选了2018年4月这个月的购买次数来做分析,其他月份的可以类推。
data_201804 = y_m_data[y_m_data['year_month'] == '2018-04']
#重命名Order Number为购买次数buy_frequency
data_201804.rename(columns={'Order Number': 'buy_frequency'}, inplace=True)
data_201804
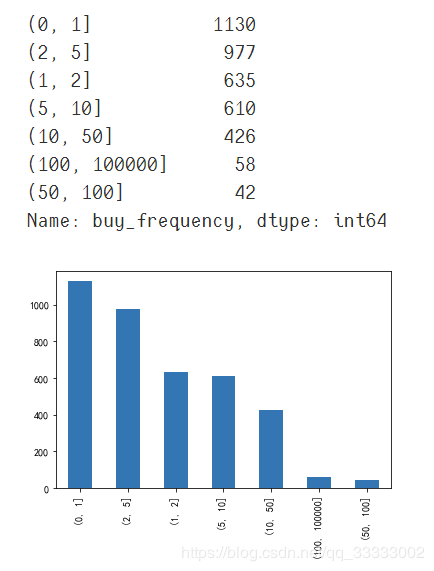
# 设置数据的区间
bins = [0, 1, 2, 5, 10, 50, 100, 100000]
per_frequency = pd.cut(data_201804['buy_frequency'], bins)
per_frequency.value_counts()
per_frequency.value_counts().plot(kind='bar')
4.3.5 RFM模型分析用户的价值
这里只针对2018年4月份的用户价值进行分类,其他可以类推。
# 按月份提取每个月用户的R、F、M值
RFM_data_all = data.groupby(['year_month',
'Client']).agg({'Order Number': 'nunique',
'Sale Date Time': 'max',
'Total': 'sum'})
RFM_data_all.reset_index(inplace=True)
# 保存一份数据,下次直接读取该数据集就可以,省时间
RFM_data_all.to_excel('RFM_data_all.xlsx', index=False)
# 提取2018年4月份的数据
RFM_data_201804 = RFM_data_all[RFM_data_all['year_month'] == '2018-04']
RFM_data_201804
输出:
# 参考时间,这里随便设置里2018-05-01 23:59:59,不让R值为0,这里的R以天作为单位
import datetime
reference_time = datetime.datetime.strptime('2018-05-01 23:59:59',
"%Y-%m-%d %H:%M:%S")
# 构建R指标
RFM_data_201804['R'] = RFM_data_201804['Sale Date Time'].apply(lambda x: (
reference_time - x).days)
# 重新命名列
RFM_data_201804.rename(columns={'Order Number': 'F', 'Total': 'M'}, inplace=True)
# 排序查看异常值
RFM_data_201804.sort_values('M', ascending=False)
输出:
这里有个异常值,标记为客户没有提及姓名的,直接删除处理。
RFM_data_201804.drop(index=26015, inplace=True)
提取RFM指标
RFM_data = RFM_data_201804[['R', 'F', 'M']]
数据规范化,进行聚类
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
#数据规范化
ss = StandardScaler()
train = ss.fit_transform(RFM_data)
# 模型进行训练,这里直接聚类成5类。
kmeans_model = KMeans(n_clusters=5)
kmeans_model.fit(train)
#查看聚类中心
test = pd.DataFrame(kmeans_model.cluster_centers_, columns=['R', 'F', 'M'])
test
输出:
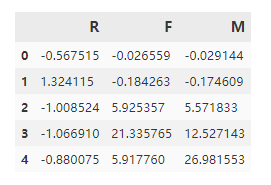
分析:
分群0:R小,F小,M小,这类属于一般价值客户。分群1,R大,F小,M小,这类属于一般发展客户。分群2,R小,R大,M大,这类属于重点保持客户。分群3、4 这类,R小,F、M大,这类都属于高价值客户。
将分群的结果合并到RFM_data数据里看下原数据。
RFM_data['sk5_label'] = kmeans_model.labels_
这里挑出分群3、4的数据来看看。
RFM_data[RFM_data['sk5_label'] == 3]
输出:
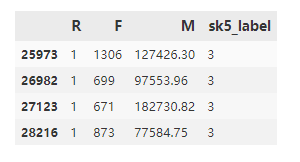
分群3的用户的购买次数F在670-1300之间,消费金额M在7.7W-18W之间,且R小,属于高价值客户。
RFM_data[RFM_data['sk5_label'] == 4]
输出:
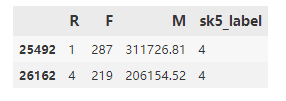
分群4的用户购买次数在210-280之间,购买金额在20W以上,这类是属于高价值客户。
Tableau实现的客户分群:
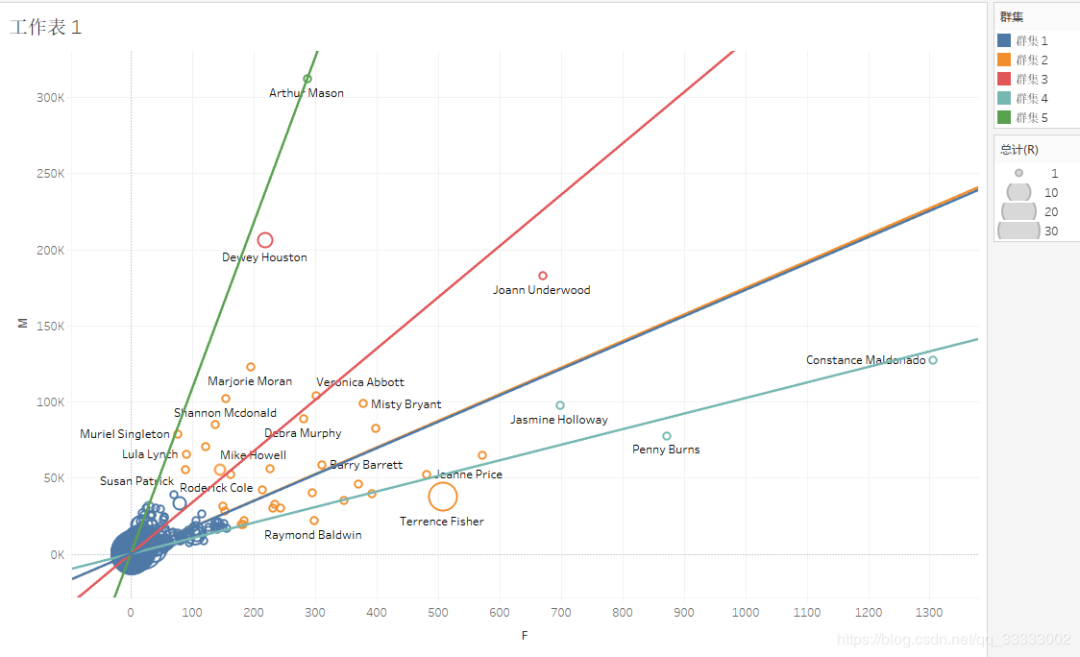
客单价=M/F。这里可以看出群集5的客单价最高,其次是群集3,最低的是群集4。
4.3.6 用户月留存率
这里统计用户月存留率是上个月与当前月都有购买的用户的数量/(除以)上个月的总用户数(去重)。类似流失率,这里不同的是都是上月流向下月的,不是1->2->3这样的流向,而是1->2, 2->3这样的流向。
# 提取每个月的用户(去重)
every_month_user = data.groupby(['year_month',
'Client']).nunique()['Order Number'].reset_index()
every_month_user
输出:
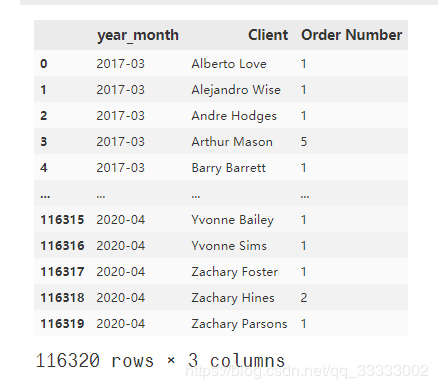
# 获取每个月份的列表,循环遍历计算上个月与当前月的留存率
year_month = every_month_user['year_month'].unique()
# 保存月留存率的列表
list_month_rate = []
for i, month in enumerate(year_month):
# 计算上个月与当前月的留存率
if i>= 1:
# 获取当前月的用户(上面groupby已去重)
this_month_client = every_month_user[every_month_user['year_month'] == month]['Client']
# 获取上个月的用户(上面groupby已去重)
previous_month_client = every_month_user[every_month_user['year_month'] == year_month[i-1]]['Client']
# 计算留存率,这里用的是上个月与当前月用户的交集个数/上个月的用户数(去重)
rate = round(len (set(this_month_client) & set(previous_month_client))
/ len(previous_month_client),2)
# 用列表保存数据,并构建DataFrame用户绘图
b = [month, rate]
list_month_rate.append(b)
# 构建DataFrame
rate_data = pd.DataFrame(list_month_rate, columns=['year_month', 'rate'])
rate_data
输出:
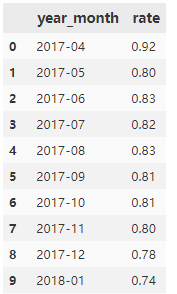
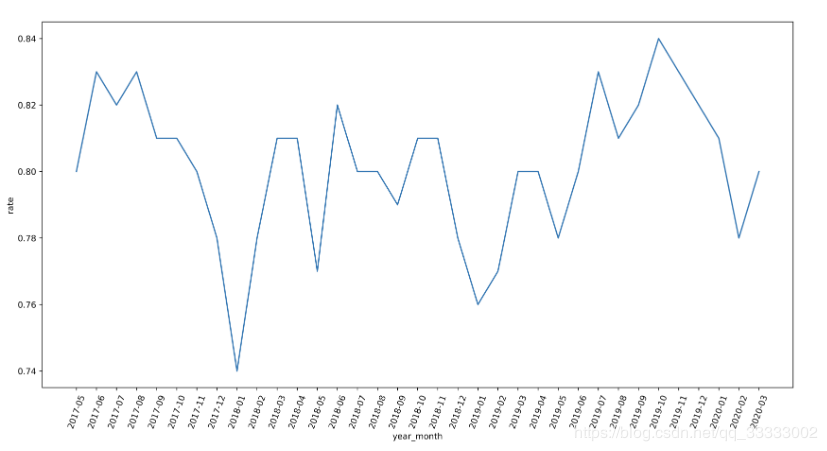
可视化:
结论:
月的用户留存率达到74%以上,用户黏性高。
4.4 产品角度
4.4.1 销售额,订单量前10的销售产品
产品Special Gasoline、Gasoline汽油类的产品的销售金额、订单量位居前列;其次是Diesel Auto Clean这个清洁类的产品。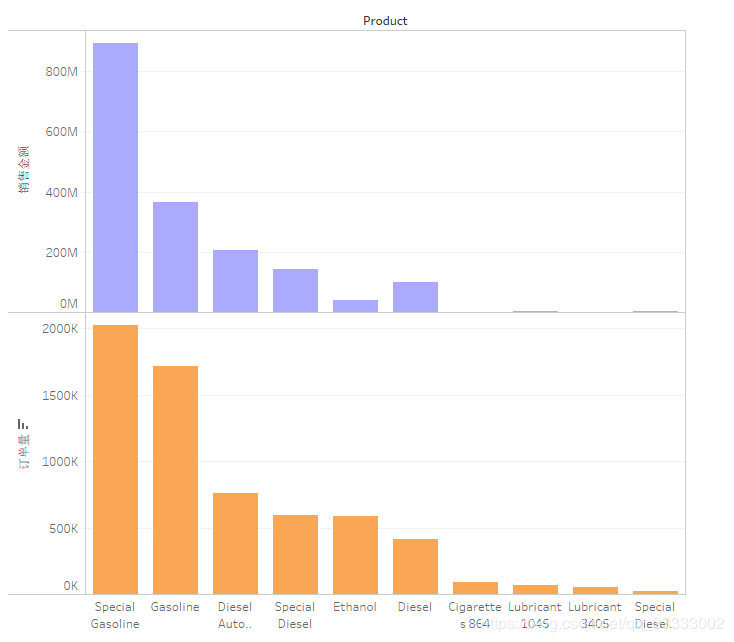
4.4.2 产品分类(聚类分析)
这里先获取每个月的产品的成本C,订单量F,销售总金额M,这里只挑选了2018年4月一个月的产品数据来分析
month_product_data = data.groupby(['year_month',
'Product']).agg({
'Product Cost': 'mean',
'Order Number': 'nunique',
'Total': 'sum'
}).reset_index()
# 重命名
month_product_data.rename(columns={'Product Cost': 'C', 'Order Number': 'F',
'Total': 'M'}, inplace=True)
# 导出数据到Excel,结合Tableau一起分析下。
month_product_data.to_excel('./month_product_data.xlsx', index=False)
# 选择2018年4月的数据
# 这里只取一个月的产品进行聚类
month_product_201804 = month_product_data[month_product_data['year_month'] == '2018-04']
month_product_201804
输出:
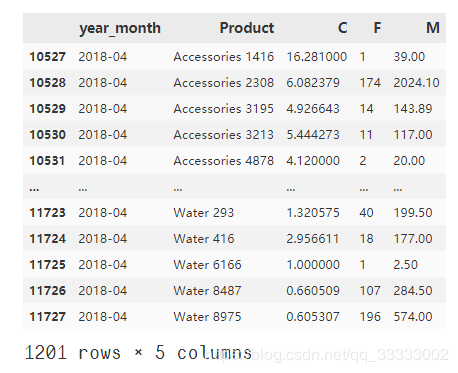
模型训练,进行聚类
# 导入包
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
ss = StandardScaler()
# 获取需要的数据
X = month_product_201804[['C', 'F', 'M']]
# 数据规范化
train_X = ss.fit_transform(X)
# 设置聚类数4个
dbscan_model = DBSCAN(min_samples=4)
# 模型训练
dbscan_model.fit(train_X)
# 将聚类的结果合并到原数据集上。
month_product_201804['labels'] = dbscan_model.labels_
# 查看聚类的分布情况
month_product_201804['labels'].value_counts()
输出:

这里标记为-1的数据集都是异常的数据,查看下。
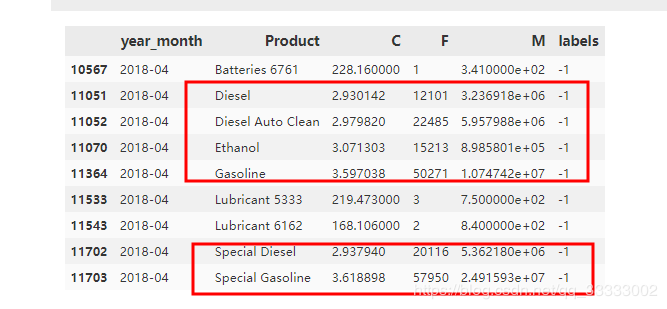
这里结合Tableau可视化看下。
这里可以看出模型标记出来为-1数据的分成两类。
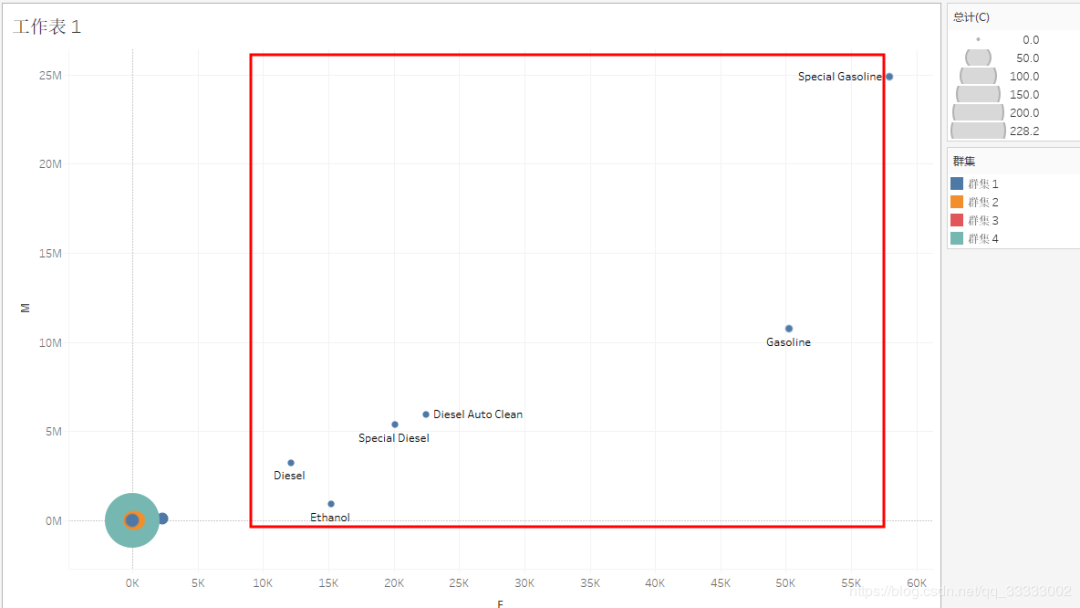
A类(上图和下图截红框):成本低,订单量多,购买金额多的,这类属于重点开发的产品。
B类:成本高,订单量少,购买金额少的,这类属于低价值的产品,应该砍掉。
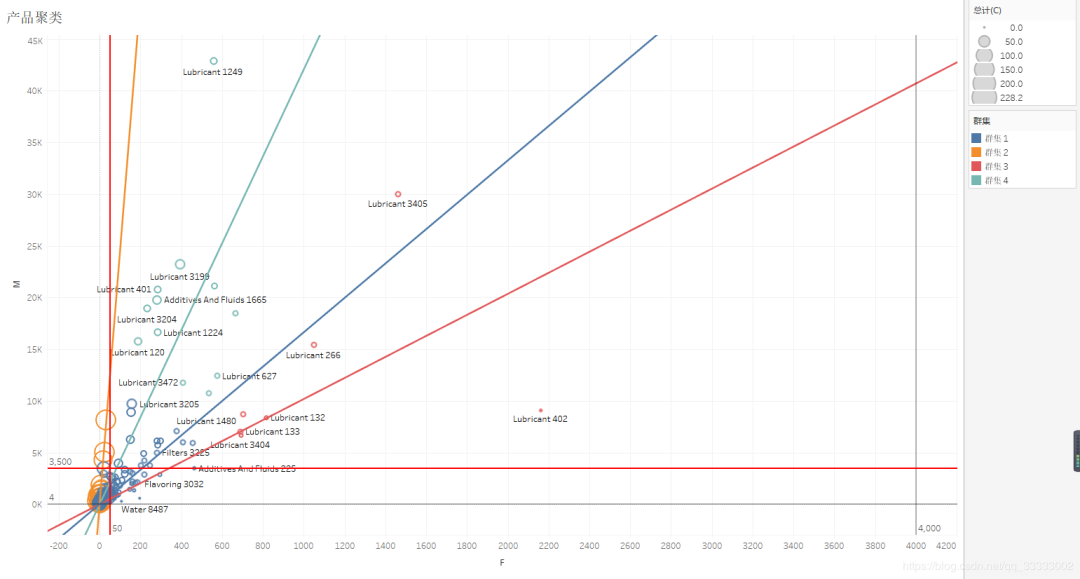
Tableau排除上图截红框的一个教特殊的产品再进行产品的聚类。
这里的圆圈的大小表示成本C的大小。
针对群集1:
这里利用二分法为订单量F分为50以下,50以上。针对F为50以下的群集1,这类购买次数较少,总的销售金额也在5K以下,这类的产品,可以采取部分下架。针对F为50以上的产品,这类产品购买次数稍多,采取维持的状态。
针对群集2:
这里也利用二分法将其分为销售金额M在3500以上,和3500以下的。3500以下的这类的产品成本高,且销售额也在3500以下,购买次数也低于50,这类产品应该采取放弃策略。3500以上的则采取先保持策略,再下一阶段再继续深入观察,分析,做进一步的决策。
针对群集3:
这类产品的购买次数F在600以上,销售金额M也在6k以上,成本C也较小,这类产品采取继续扩大。
针对群集4:
成本C较小,购买次数F在200-600之间,销售金额在10K以上,这类产品属于重点保持的产品,该类产品应给与较大的重视,进一步发挥这类产品的价值。
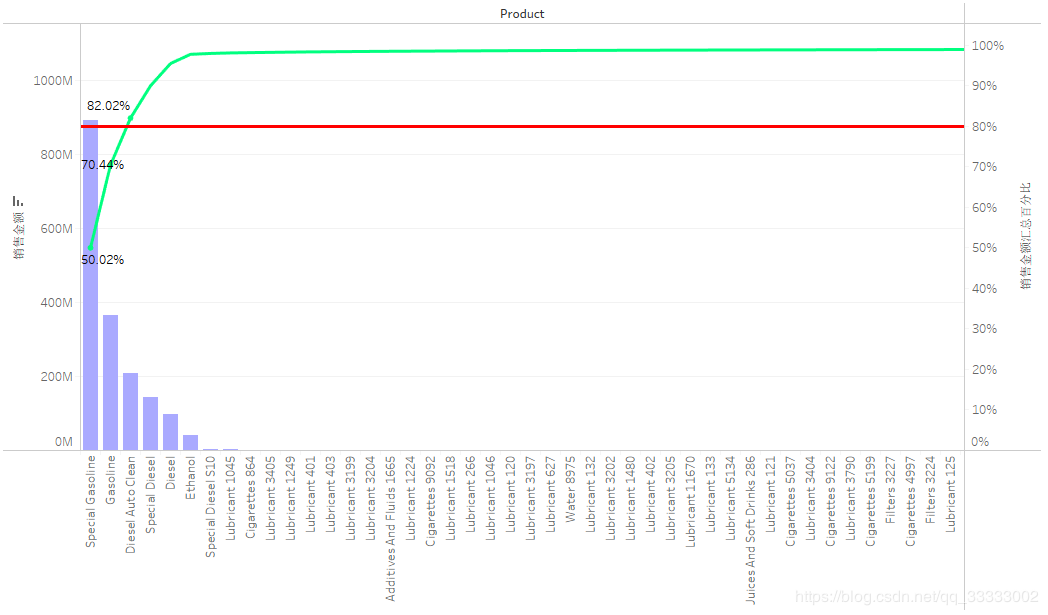
4.4.3 产品销售额情况及总体的占比(帕累托最优)
产品的头部的效应明显,前三产品的总销售金额达到总销售金额的82%以上,符合二八定律。
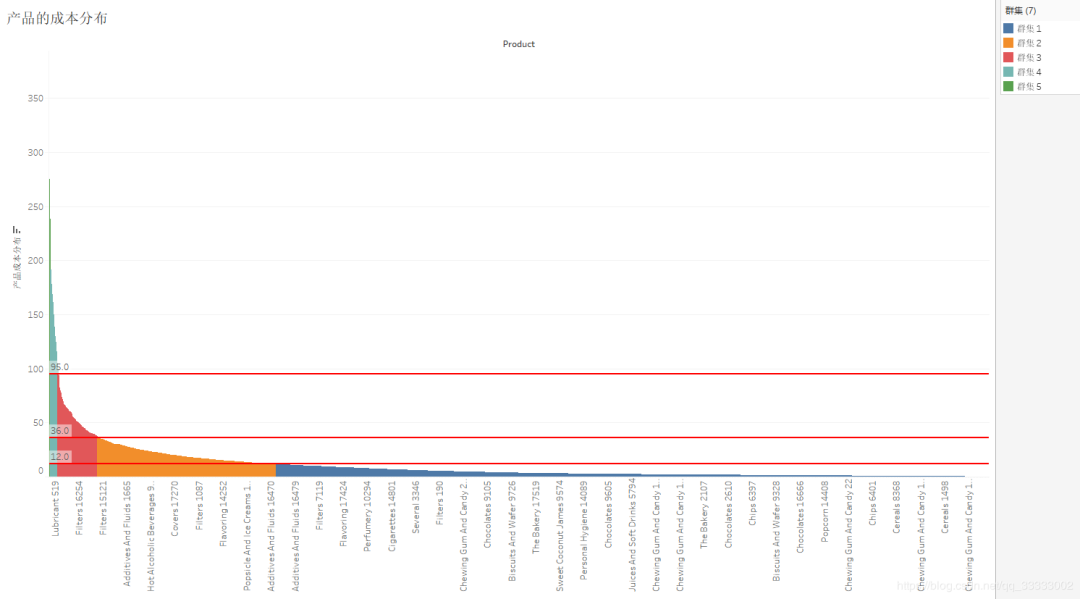
4.4.4 产品的成本分布
较大一部分产品的成本在12以下,其次是在12-36区间,接着是36-95的区间,95以上的产品较少。
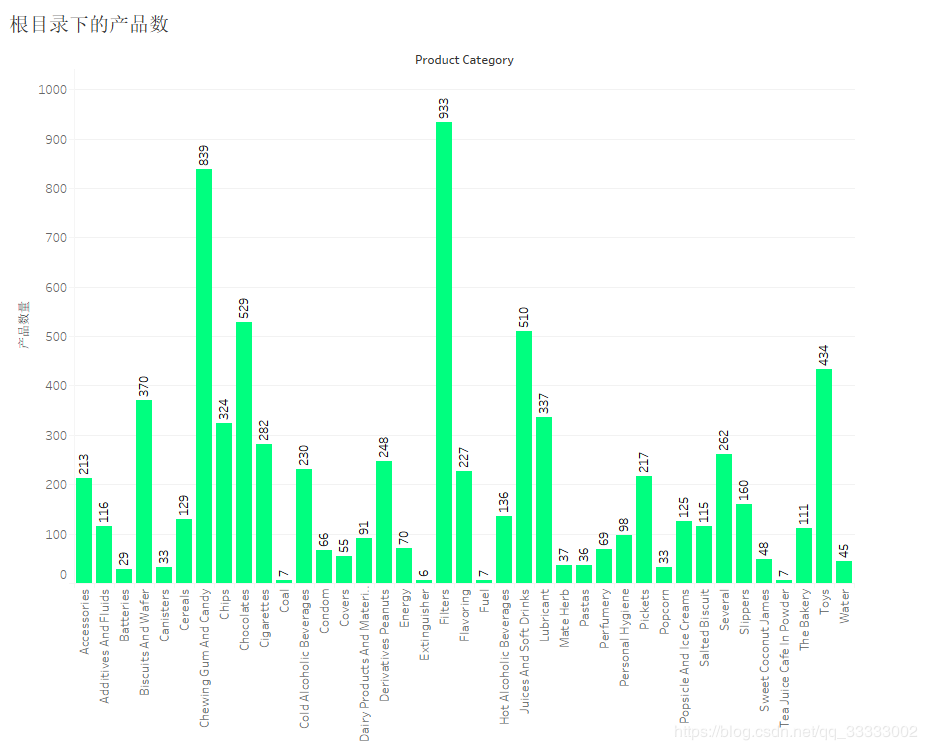
4.4.5 跟目录下的各个产品数
Filters产品类别下的产品数最多,达到933。其次是839的Chewing Gum And Candy。最少的产品数的是类别Extinguisher,只有6个。
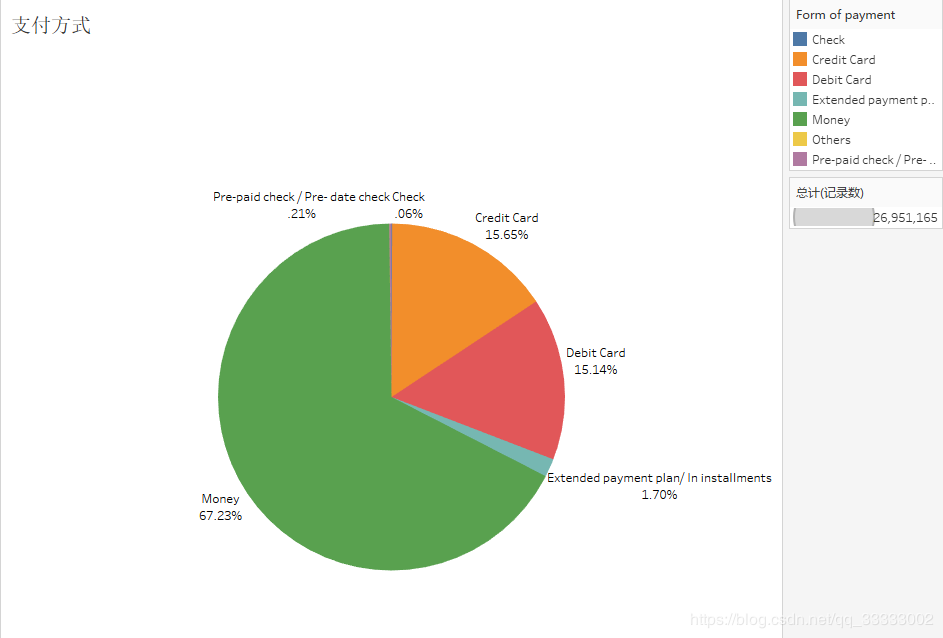
5 支付方式
近7成的用户选择现金支付。