八十二、归并排序求取复杂的逆序数
「@Author:Runsen」
逆序数,我在很多的面试题都见过,本质上来说难度是比较大,因为如果使用暴力法当数据量一大,必然就会爆掉。你现在就要记住逆序数就是考归并排序。
逆序数
给定一个数组array[0,...,n-1], 若对于某两个元素array[i],array[j],若i
则认为array[i],array[j]是逆序对。一个数组中包含的逆序对的数目称为该数组的逆序数。设计一个算法求一个数组的逆序数
比如给出数组nums = [11, 8, 3, 9, 7, 1, 2, 5],我可以求出[(11, 8), (8, 3), (11, 3), (11, 9), (7, 1), (7, 2), (7, 5), (3, 1), (8, 1), (9, 1), (11, 1), (3, 2), (8, 2), (9, 2), (11, 2), (8, 5), (9, 5), (11, 5), (8, 7), (9, 7), (11, 7)]
采用暴力破解的话,代码非常简单。
r = []
def reversePairs(nums):
size = len(nums)
if size < 2:
return 0
res = 0
for i in range(0, size - 1):
for j in range(i + 1, size):
if nums[i] > nums[j]:
res += 1
r.append([nums[i],nums[j]])
return res
print(reversePairs([11, 8, 3, 9, 7, 1, 2, 5]))
print(r)
21
[[11, 8], [11, 3], [11, 9], [11, 7], [11, 1], [11, 2], [11, 5], [8, 3], [8, 7], [8, 1], [8, 2], [8, 5], [3, 1], [3, 2], [9, 7], [9, 1], [9, 2], [9, 5], [7, 1], [7, 2], [7, 5]]
归并排序
「下面说下归并排序的思路。」 我们可以在归并排序的基础上, 完成对逆序对的个数统计.
归并排序的过程:
将数组拆分成左右两个部分 对左边进行归并排序 对右边进行归并排序 合并左右两边
我们可以发现一点, 完成第三步操作之后,并不会改变这样的逆序对(一个数在左边,另一个数在右边)的个数.
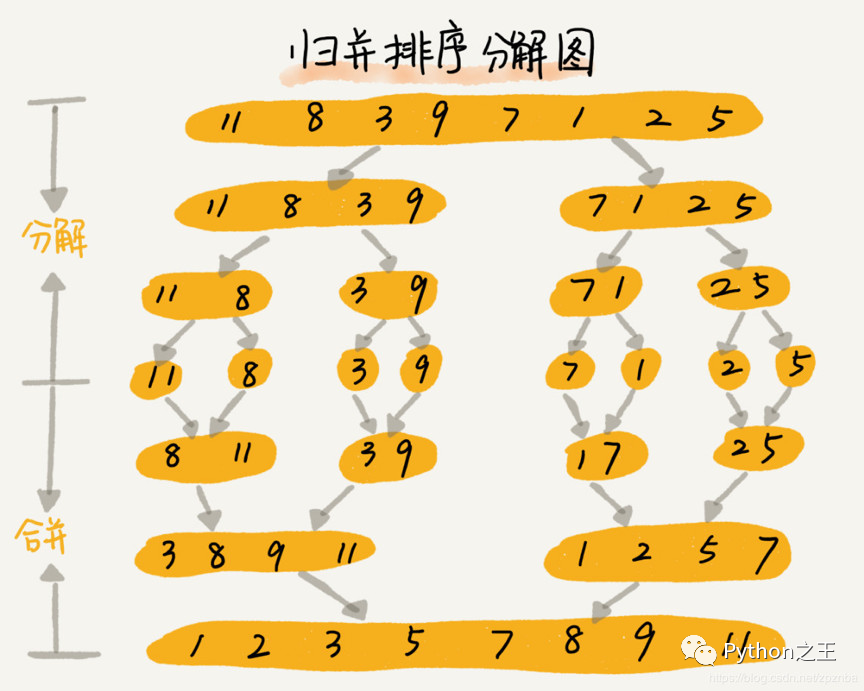
因此逆序对统计的过程为:
将数组拆分成左右两个部分 对左边进行归并排序,并返回左边的逆序对个数leftCount 。比如,11和8是一个,3和9不是,继续,8和3是一个,8和9不是一个,11和3是一个,11和9也是一个,因此leftCount = 4 对右边进行归并排序,并返回右边的逆序对个数rightCount=3 。 合并左右两边,并计算这样的逆序对(一个数在左边,另一个数在右边)个数crossCount 14. 数组的逆序对个数为: leftCount + rightCount + crossCount = 21.
利用归并排序计算逆序数对的方法太巧妙了,但是只要提醒你一下使用分治思想,或者使用归并排序思想解决这道问题你可能就有思路了。归并排序实际上会把数组分成两个有序部分,我们不妨称其为左和右,归并排序的过程中会将左右两部分合并成一个有序的部分,对于每一个左右部分,我们分别计算其逆序数,然后全部加起来就是我们要求的逆序数,详细的思路在代码中注释了。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公众号:Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/12/25
'''
temp = [0] * 100
count = [0]
pairs = []
def Merge(nums, low, mid, high):
i = low
j = mid + 1
size = 0
while i <= mid and j <= high:
if nums[i] < nums[j]:
temp[size] = nums[i]
i += 1
else:
# 除了以下三行代码,其余代码与归并排序一模一样
count[0] += (mid - i + 1)
for h in range(i, mid + 1):
pairs.append((nums[h], nums[j]))
temp[size] = nums[j]
j += 1
size += 1
while i <= mid:
temp[size] = nums[i]
size += 1
i += 1
while j <= high:
temp[size] = nums[j]
size += 1
j += 1
for i in range(size):
nums[low + i] = temp[i]
def Merge_sort(nums, low, high):
if low >= high:
return
mid = (low + high) >> 1
Merge_sort(nums, low, mid)
Merge_sort(nums, mid + 1, high)
# 此时是排好序
Merge(nums, low, mid, high)
if __name__ == '__main__':
nums = [11, 8, 3, 9, 7, 1, 2, 5]
Merge_sort(nums, 0, len(nums) - 1)
print(pairs)
print(count)
[(11, 8), (8, 3), (11, 3), (11, 9), (7, 1), (7, 2), (7, 5), (3, 1), (8, 1), (9, 1), (11, 1), (3, 2), (8, 2), (9, 2), (11, 2), (8, 5), (9, 5), (11, 5), (8, 7), (9, 7), (11, 7)]
[21]
该题对标的是Leetcode:剑指 Offer 51. 数组中的逆序对
比如[3,4,1,5,2]
https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
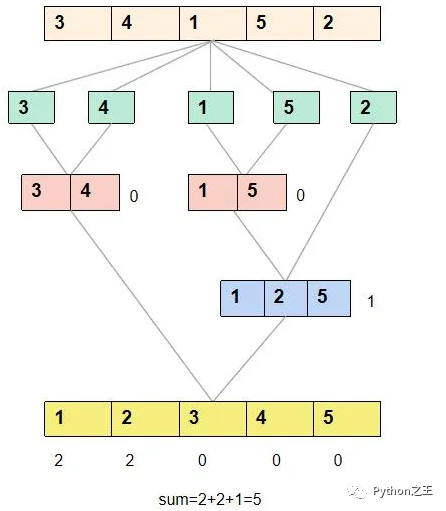
具体代码和上面代码差不多,下面代码来源Leetcode官网。
class Solution:
def reversePairs(self, nums: List[int]) -> int:
self.cnt = 0
def merge(nums, start, mid, end):
i, j, temp = start, mid + 1, []
while i <= mid and j <= end:
if nums[i] <= nums[j]:
temp.append(nums[i])
i += 1
else:
self.cnt += mid - i + 1
temp.append(nums[j])
j += 1
while i <= mid:
temp.append(nums[i])
i += 1
while j <= end:
temp.append(nums[j])
j += 1
for i in range(len(temp)):
nums[start + i] = temp[i]
def mergeSort(nums, start, end):
if start >= end: return
mid = (start + end) >> 1
mergeSort(nums, start, mid)
mergeSort(nums, mid + 1, end)
merge(nums, start, mid, end)
mergeSort(nums, 0, len(nums) - 1)
return self.cnt
好了,今天的分享就到这了!
本文已收录 GitHub,传送门~[1] ,里面更有大厂面试完整考点,欢迎 Star。
参考资料
传送门~: https://github.com/MaoliRUNsen/runsenlearnpy100
更多的文章
点击下面小程序
- END -

