【04】-01为什么需要四颗卫星才能定位

关于什么是GPS我们就不赘述了，可以参考【04】无人驾驶的定位（Localization）一文。今天我们来讲讲GPS定位为什么需要4颗近地卫星才行，而不是3颗。

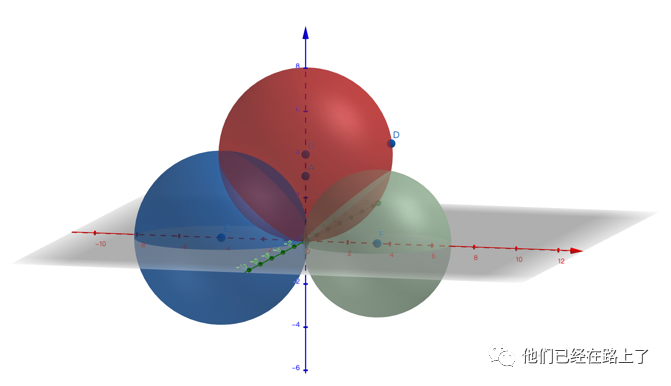
我们先来看一个数学问题，从数学逻辑上来讲，我们知道卫星到地面某点的距离，以该距离为半径，以卫星位置为球心画球，此时需要三个卫星，也就是三个球体就可以得到两个交点，如下图所示：

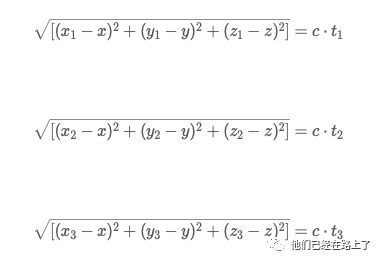
• 卫星1的坐标：（x1，y1，z1）；
• GPS接收器坐标：（x，y，z）；
• 光速：c
• 卫星信号到GPS接收器的时间：t1、t2、t3；

当我们排除掉一个不在地球表面的点之后，剩下的点就是地面的点了。

但是这只是数学理论，由于卫星和GPS接收器的时间没有办法保持完全一致，这个计算过程就存在一个新的未知变量，也就是GPS接收器和标准时间的差异，我们来看一个例子：

由于GPS接收器的时间和卫星的时间都不是标准时间，都有误差，我们假设：标准时间是8：00，接收机时间是8：01，卫星是8：02，卫星发射电磁波到接收机的时间要5分钟。在标准时间8：00的时候，卫星以为时间是8：02，所以它发射一个信号“我是在卫星时间8：02发射信号的”。接收机将在（标准时间8:05接收到信号），但此时接收机是时间8：01，因此它在自己的时间的8：06接收到了信号，所以，接收机就认为时间为8：06-8：02=4分钟，信号传播了4分钟，而实际上，信号传播了5分钟，这种误差显然是巨大的。

因此我们将计算公式进行优化，引入GPS接收器的时间、卫星时间、标准时间，于是公式如下：

• 卫星1的坐标：（x1，y1，z1）； 
• 卫星1的时间：t1； 
• 卫星1的钟差：t-w，即卫星时间与标准时间的偏差；
• GPS接收器坐标：（x，y，z）； 
• GPS接收器的时间：T； 
• GPS接收器的钟差：t-g，即GPS接收器时间与标准时间的偏差； 
• 光速：c

在这个公式里，卫星时间可以根据卫星的原子钟来获得，卫星的钟差同样可以如此获得，卫星的坐标可以通过星历获得，以上这些信息都是已知道的，那么未知的就剩x、y、z、t-g了，因此这时候可以通过四个方程得到x、y、z的解。

当然了还有一个思路就是在GPS接收器上也安装类似卫星的高精度时钟来保证时间统一，但是这个成本其实是非常大的，所以通常的解决方法就是再引入一颗卫星来解决这个问题。