(多图预警)这就是那个著名的接雨水
接雨水今天给大家带来的是一道特别特别特别经典的题目接雨水问题,这个问题是很多算法书上面举例过的题目。虽然是难度题,但是相对来说还是比较容易理解的,代码长度也适中,说了这么多,就一个意思,大家记得打卡这个题目啊,真的是很nice的一道题,下面我们来看一下题目描述。给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
示例3:
输入:[4,3,2,0,1,1,5]
输出:13
说明:上面是由数组 [4,3,2,0,1,1,5]表示的高度图,在这种情况下,可以接 13个单位的雨水(见下图)。
题目解析:
看了上面的示例刚开始刷题的同学可能有些懵逼,那我们结合图片来理解一下,我们就用示例3的例子进行举例,他的雨水到底代表的是什么。输入代表的是黄色箱子的个数,蓝色箱子代表雨水数量。缝隙之间可以装多少水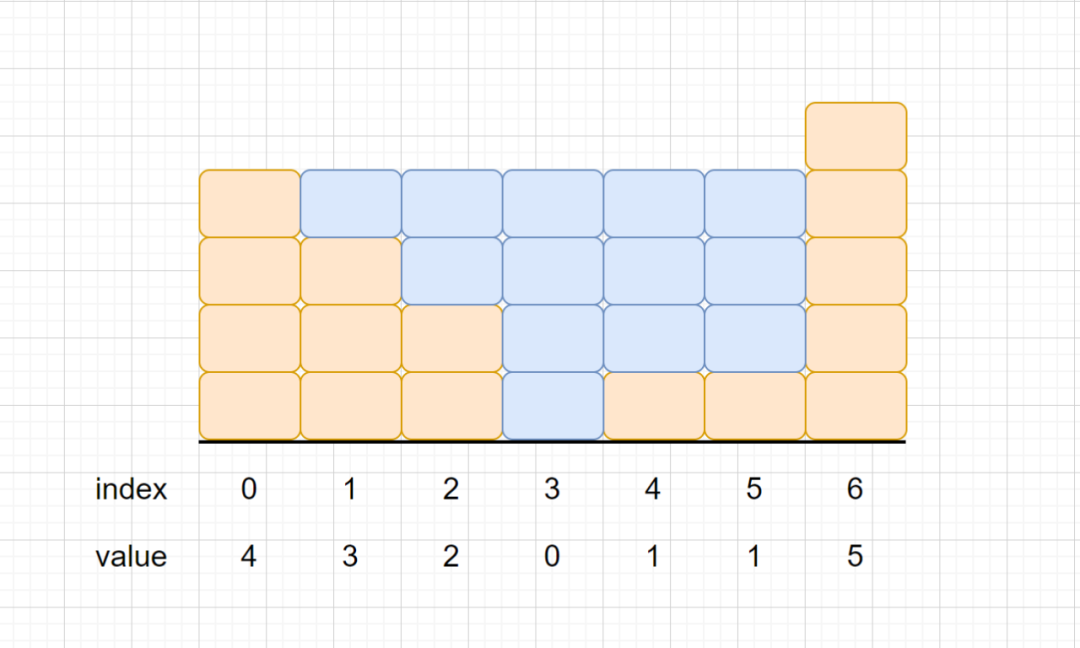
上图则为我们的题目描述,是不是理解了呢?你也可以这样理解我们在地上放置了若干高度的黄色箱子,他们中间有空隙,然后我们想在他们里面插入若干蓝色箱子,并保证插入之后,这些箱子的左视图和右视图都不能看到蓝色箱子。好啦题目我们已经理解了,下面我们看一下解题思路。做这个题前我们可以先去看一下我们之前做过的另一道题目每日温度。这两道题目的思路差不多,都是利用了单调栈的思想,下面我们来看一下具体思路吧。这里我们也系统的说一下单调栈,单调栈含义就是栈内的元素是单调的,我们这两个题目用到的都是递减栈(相同也可以),我们依次将元素压入栈,如果当前元素小于或等于栈顶元素则入栈,如果大于栈顶元素则先将栈顶不断出栈,直到当前元素小于或等于栈顶元素为止,然后再将当前元素入栈。就比如下图的4,想入栈的话则需要2,3出栈之后才能入栈,因为4大于他俩。
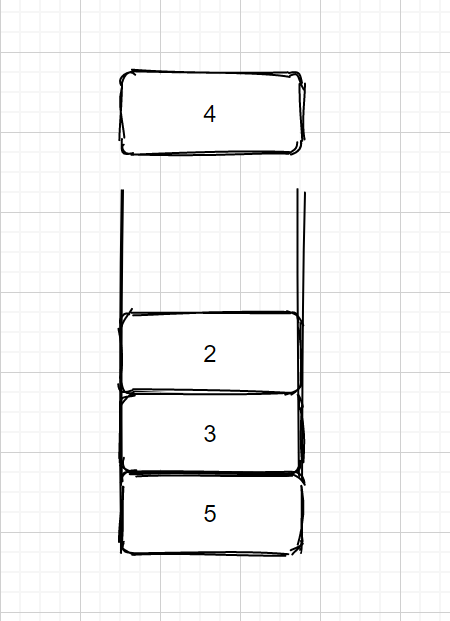
我们了解单调栈的含义下面我们来看一下接雨水问题到底该怎么做,其实原理也很简单,我们通过我们的例3来进行说明。首先我们依次入栈4,3,2,0我们的数组前四个元素是符合单调栈规则的。但是我们的第五个1,是大于0的。那我们就需要0出栈1入栈。但是我们这样做是为了什么呢?有什么意义呢?别急我们来看下图。
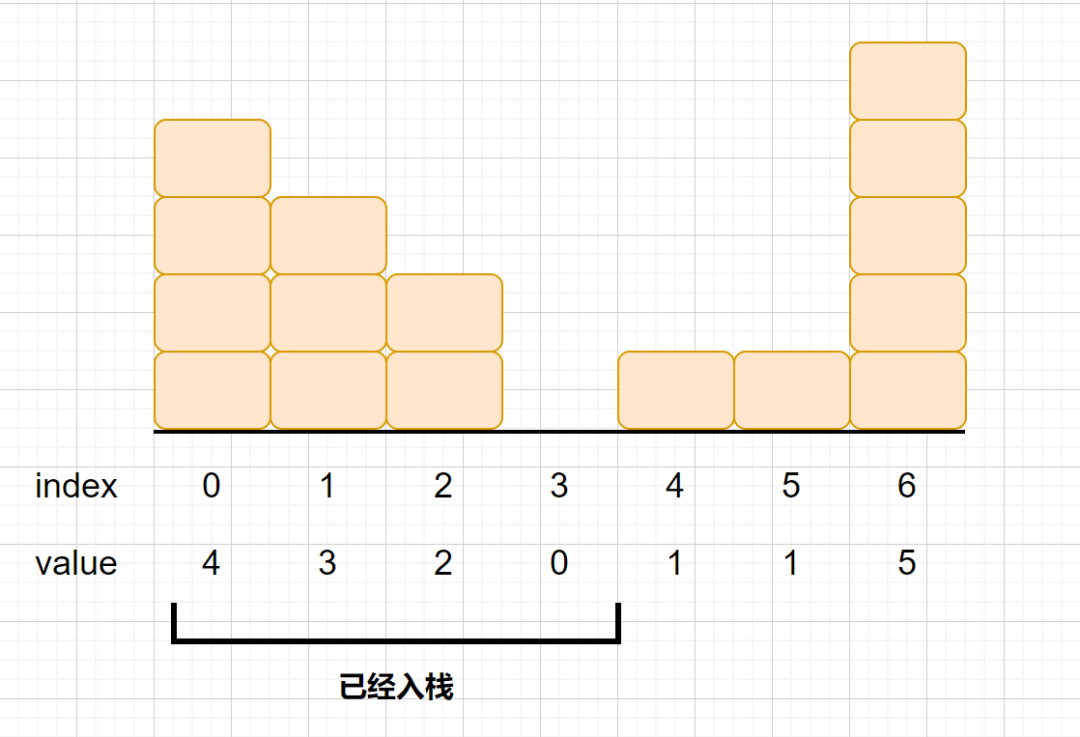
上图我们的,4,3,2,0已经入栈了,我们的另一个元素为1,栈顶元素为0,栈顶下的元素为2。那么我们在这一层接到的雨水数量怎么算呢?2,0,1这三个元素可以接住的水为一个单位(见下图)这是我们第一层接到水的数量。注:能接到水的情况,肯定是中间低两边高的情况
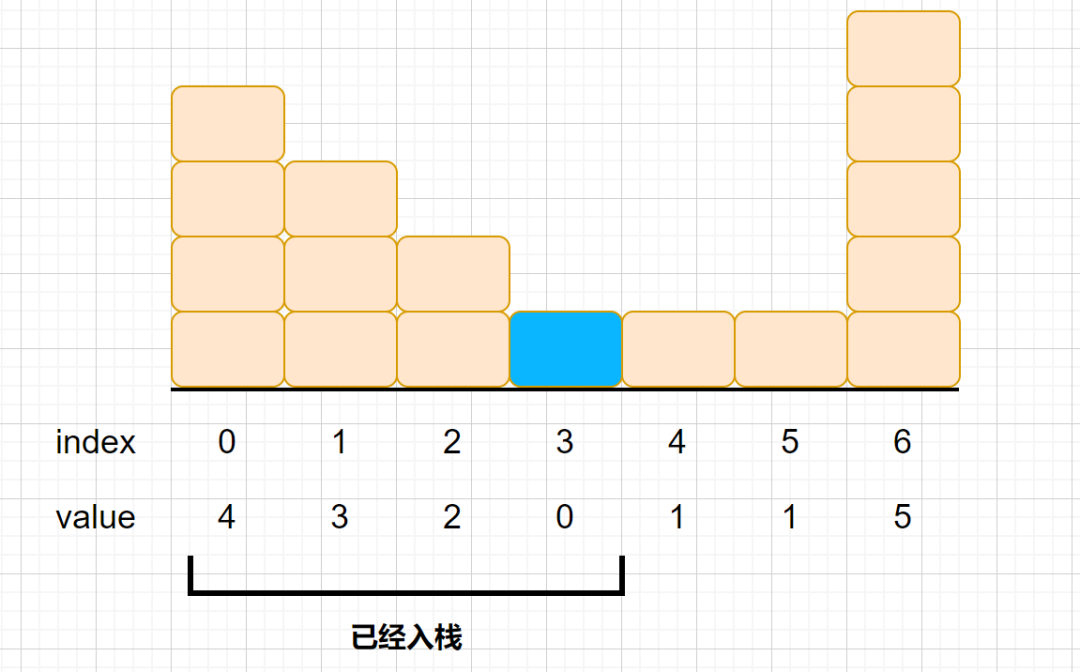
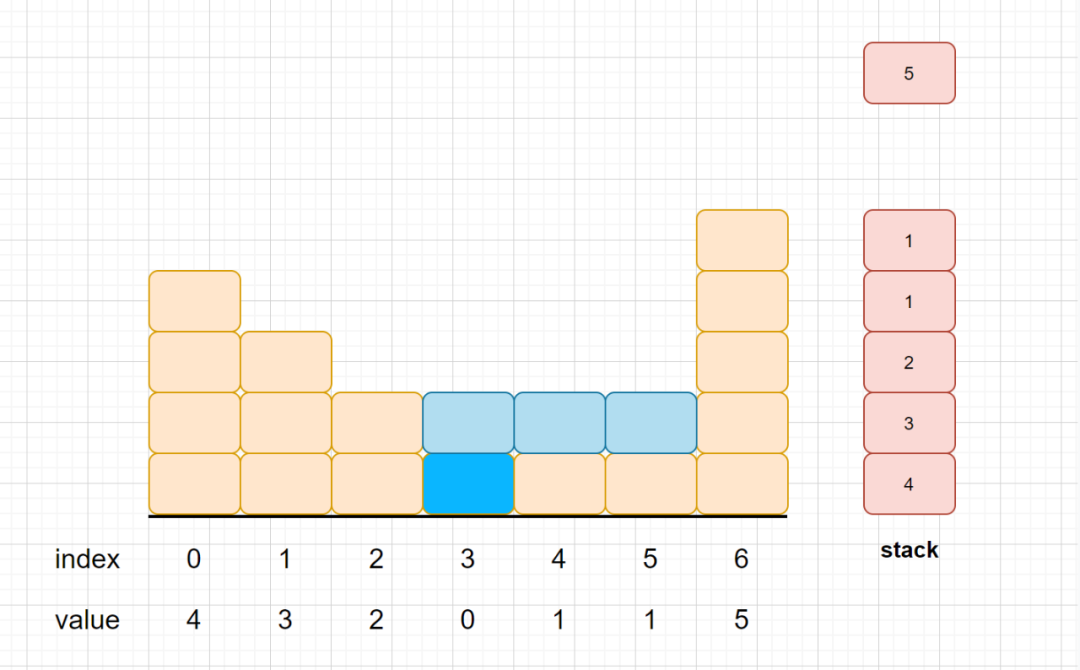
我们是通过2,1,1,5这四个元素求得第二层的接水数为1*3=3;1是因为min(2-1,5-1)=min(1,4)得来的,大家可以思考一下木桶效应。装水的多少,肯定是按最短的那个木板来的,所以高度为1,3的话是因为5的索引为6,2的索引为2,他们之间共有三个元素(3,4,5)也就是3个单位。所以为6-2-1=3。将1出栈之后,我们栈顶元素就变成了2,下一元素变成了3,那么3,2,5这三个元素同样也可以接到水。
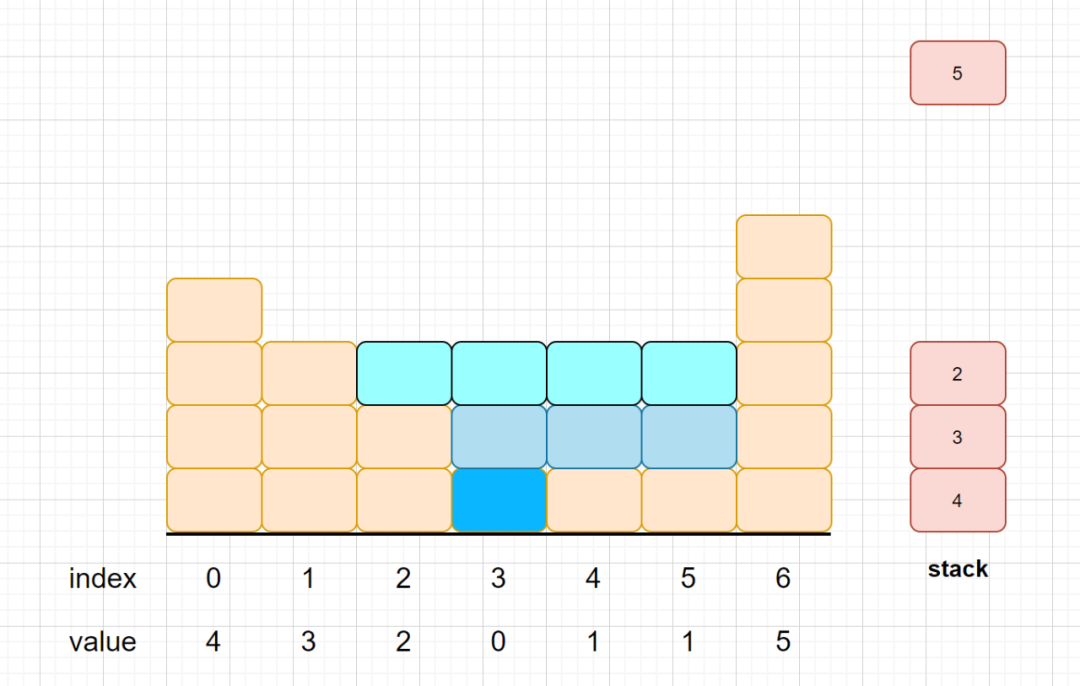
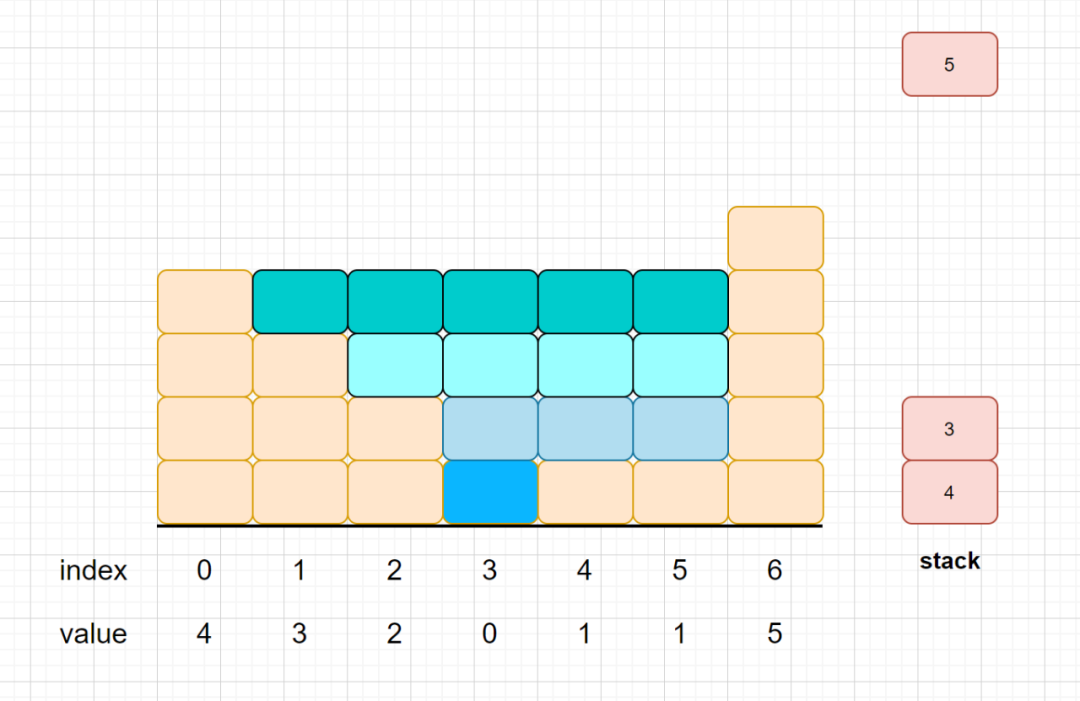
这是我们第四层接水的情况,一共能够接到5个单位的水,那么我们总的接水数加起来,那就是1+3+4+5=13。你学会了吗?别急还有动图我们,我们再来深入理解一哈。
题目代码:
class Solution {
public int trap(int[] height) {
Stack stack = new Stack();
int water = 0;
//特殊情况
if(height.length < 3){
return 0;
}
for(int i = 0; i < height.length; i++){
while(!stack.isEmpty() && height[i] > height[stack.peek()])
//栈顶元素
int popnum = stack.pop();
//相同元素的情况例1,1
while(!stack.isEmpty()&&height[popnum] == height[stack.peek()]){
stack.pop();
}
//计算该层的水的单位
if(!stack.isEmpty()){
int temp = height[stack.peek()];//栈顶元素值
//高
int hig = Math.min(temp-height[popnum],height[i]-height[popnum]);
//宽
int wid = i-stack.peek()-1;
water += hig * wid;
}
}
//这里入栈的是索引
stack.push(i);
}
return water;
}
}
这个题解的图片太多了,整了挺久,因为怕浪费了这道经典题,所以画了很多图片进行说明,希望可以帮到大家。
来个直击灵魂的三连吧!
评论
