漫谈分布式共识问题
混乱的“一致性”问题
Consensus != Consistency
受翻译影响,网上很多讨论 paxos 或 raft 的博客使用“分布式一致性协议”或者“分布式一致性算法”这样的字眼,虽然在汉语中“达成共识”和“达成一致”是一个意思,但是必须要说明在这里讨论的是 consensus 问题,使用“共识”来表达更清晰一些。而 CAP 定理中的 C 和数据库 ACID 的 C 才是真正的“一致性”—— consistency 问题,尽管这两个 C 讨论的也不是同一个问题,但在这里不展开。
为了规范和清晰表达,在讨论 consensus 问题的时候统一使用“共识”一词。
注:在早些的文献中,共识(consensus)也叫做协商(agreement)。
共识问题
那么共识问题到底是什么呢?举个生活中的例子,小明和小王出去聚会,小明问:“小王,我们喝点什么吧?” 小王:“喝咖啡怎么样?” 小明:“好啊,那就来杯咖啡。”
在上面的场景中,小王提议喝一杯咖啡,小明表示同意,两人就“喝杯咖啡”这个问题达成共识,并根据这个结果采取行动。这就是生活中的共识。
在分布式系统中,共识就是系统中的多个节点对某个值达成一致。共识问题可以用数学语言来描述:一个分布式系统包含 n 个进程 {0, 1, 2,..., n-1},每个进程都有一个初值,进程之间互相通信,设计一种算法使得尽管出现故障,进程们仍协商出某个不可撤销的最终决定值,且每次执行都满足以下三个性质:
•终止性(Termination):所有正确的进程最终都会认同某一个值。•协定性(Agreement):所有正确的进程认同的值都是同一个值。•完整性(Integrity),也称作有效性(Validity):如果正确的进程都提议同一个值,那么所有处于认同状态的正确进程都选择该值。
完整性可以有一些变化,例如,一种较弱的完整性是认定值等于某些正确经常提议的值,而不必是所有进程提议的值。完整性也隐含了,最终被认同的值必定是某个节点提出过的。
为什么要达成共识?
我们首先介绍分布式系统达成共识的动机。
在前文中,我们已经了解到分布式系统的几个主要难题:
•网络问题•时钟问题•节点故障问题
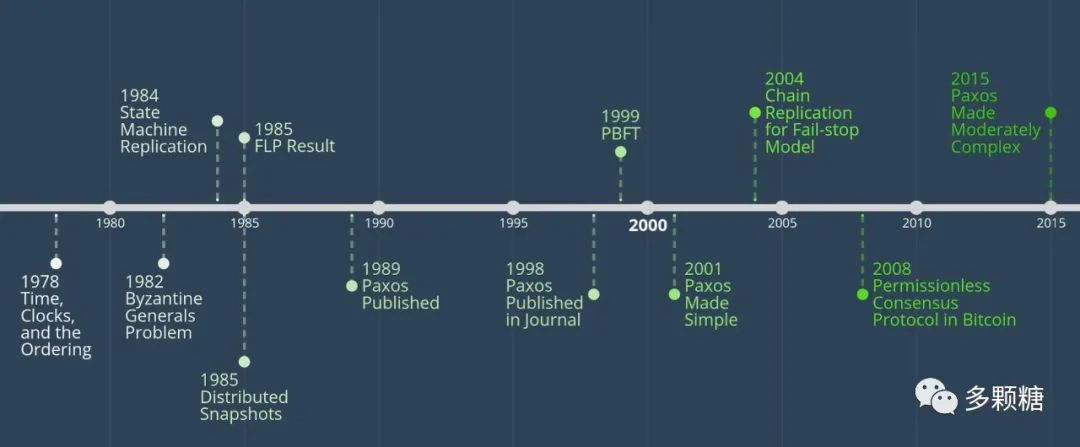
第一篇提到共识问题的文献[1] 来自于 lamport 的 "Time, Clocks and the Ordering of Events in a Distributed System[2]",尽管它并没有明确的提出共识(consensus)或者协商(agreement)的概念。论文阐述了在分布式系统中,你无法判断事件 A 是否发生在事件 B 之前,除非 A 和 B 存在某种依赖关系。由此还引出了分布式状态机的概念。
在分布式系统中,共识就常常应用在这种多副本状态机(Replicated state machines),状态机在每台节点上都存有副本,这些状态机都有相同的初始状态,每次状态转变、下个状态是什么都由相关进程共同决定,每一台节点的日志的值和顺序都相同。每个状态机在“哪个状态是下一个需要处理的状态”这个问题上达成共识,这就是一个共识问题。
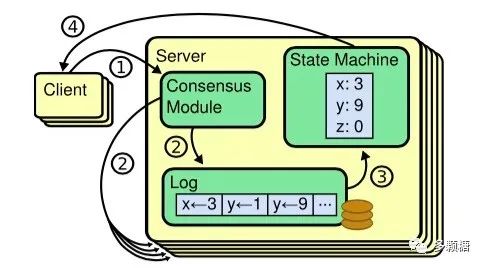
最终,这些节点看起来就像一个单独的、高可靠的状态机。Raft 的论文[3]提到,使用状态机我们就能克服上述三个问题:
•满足在所有非拜占庭条件下确保安全(不会返回错误结果),包括网络延迟、分区、丢包、重复和重排序。•不依赖于时序。•高可用。只要集群中的大部分节点正常运行,并能够互相通信且可以同客户端通信,这个集群就完全可用。因此,拥有5个节点的集群可以容忍其中的2个节点失败。假使通过停掉某些节点使其失败,稍后它们会从持久化存储的状态进行恢复,并重新加入到集群中。
不仅如此,达成共识还可以解决分布式系统中的以下经典问题:
•互斥(Mutual exclusion):哪个进程进入临界区访问资源?•选主(Leader election):在单主复制的数据库,需要所有节点就哪个节点是领导者达成共识。如果一些由于网络故障而无法与其他节点通信,可能会产生两个领导者,它们都会接受写入,数据就可能会产生分歧,从而导致数据不一致或丢失。•原子提交(Atomic commit):跨多节点或跨多分区事务的数据库中,一个事务可能在某些节点上失败,但在其他节点上成功。如果我们想要维护这种事务的原子性,必须让所有节点对事务的结果达成共识:要么全部提交,要么全部中止/回滚。
总而言之,在共识的帮助下,分布式系统就可以像单一节点一样工作——所以共识问题是分布式系统最基本的问题。
系统模型
在考虑如何达成共识之前,需要考虑分布式系统中有哪些可供选择的计算模型。主要有以下几个方面:
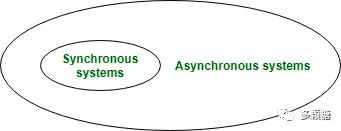
网络模型:
•同步(Synchronous):响应时间是在一个固定且已知的有限范围内。•异步(Asynchronous):响应时间是无限的。
故障类型:
•Fail-stop failures:节点突然宕机并停止响应其它节点。•Byzantine failures[4]:源自“拜占庭将军问题” ,是指节点响应的数据会产生无法预料的结果,可能会互相矛盾或完全没有意义,这个节点甚至是在“说谎”,例如一个被黑客入侵的节点。
消息模型:
•口头消息(oral messages):消息被转述的时候是可能被篡改的。•签名消息(signed messages):消息被发出来之后是无法伪造的,只要被篡改就会被发现。
作为最常见的,我们将分别讨论在同步系统和异步系统中的共识。在同步通信系统中达成共识是可行的(下文将会谈论这点),但是,在实际的分布式系统中同步通信是不切实际的,我们不知道消息是故障了还是延迟了。异步与同步相比是一种更通用的情况。一个适用于异步系统的算法,也能被用于同步系统,但是反过来并不成立。
让我们先从异步的情况开始。
异步系统中的共识
FLP 不可能(FLP Impossibility)
早在 1985 年,Fischer、Lynch 和 Paterson (FLP)在 "Impossibility of Distributed Consensus with One Faulty Process[5]" 证明了:在一个异步系统中,即使只有一个进程出现了故障,也没有算法能保证达成共识。

简单来说,因为在一个异步系统中,进程可以随时发出响应,所以没有办法分辨一个进程是速度很慢还是已经崩溃,这不满足终止性(Termination)。详细的证明已经超出本文范围,不在细述。
此时,人们意识到一个分布式共识算法需要具有的两个属性:安全性(safety)和活性(liveness)。安全性意味着所有正确的进程都认同同一个值,活性意味着分布式系统最终会认同某一个值。每个共识算法要么牺牲掉一个属性,要么放宽对网络异步的假设。
虽然 FLP 不可能定理听着让人望而生畏,但也给后来的人们提供了研究的思路——不再尝试寻找异步通信系统中共识问题完全正确的解法。FLP 不可能是指无法确保达成共识,并不是说如果有一个进程出错,就永远无法达成共识。这种不可能的结果来自于算法流程中最坏的结果:
•一个完全异步的系统•发生了故障•最后,不可能有一个确定的共识算法。
针对这些最坏的情况,可以找到一些方法,尽可能去绕过 FLP 不可能,能满足大部分情况下都能达成共识。《分布式系统:概念与设计》[6]提到一般有三种办法:
1.故障屏蔽(Fault masking)2.使用故障检测器(Failure detectors)3.使用随机性算法(Non-Determinism)
1、故障屏蔽(Fault masking)
既然异步系统中无法证明能够达成共识,我们可以将异步系统转换为同步系统,故障屏蔽就是第一种方法。故障屏蔽假设故障的进程最终会恢复,并找到一种重新加入分布式系统的方式。如果没有收到来自某个进程的消息,就一直等待直到收到预期的消息。
例如,两阶段提交事务使用持久存储,能够从崩溃中恢复。如果一个进程崩溃,它会被重启(自动重启或由管理员重启)。进程在程序的关键点的持久存储中保留了足够多的信息,以便在崩溃和重启时能够利用这些数据继续工作。换句话说故障程序也能够像正确的进程一样工作,只是它有时候需要很长时间来执行一个恢复处理。
故障屏蔽被应用在各种系统设计中。
2、使用故障检测器(Failure detectors)
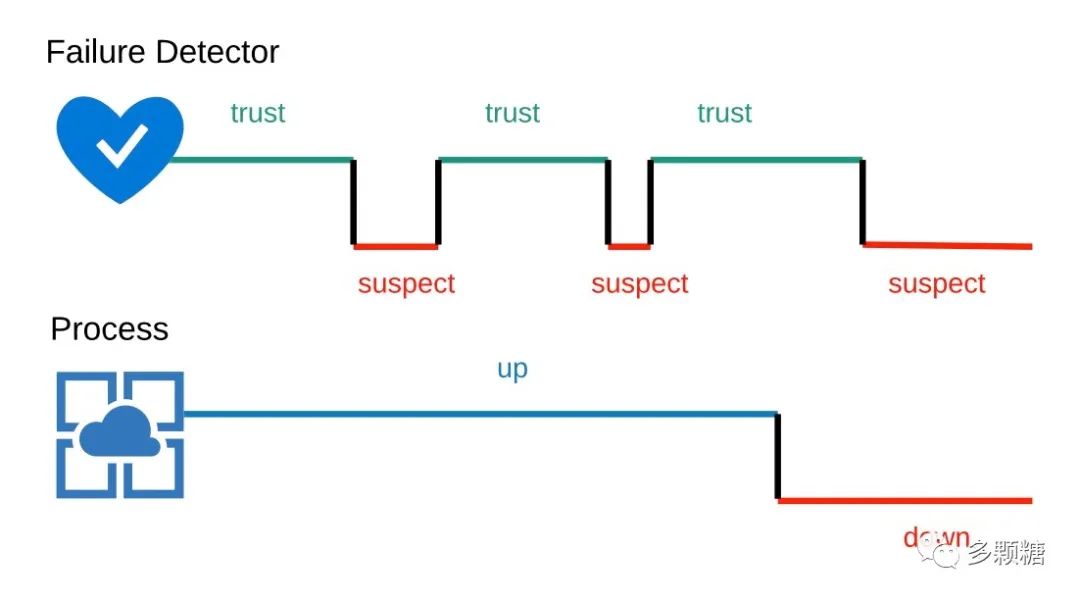
将异步系统转换为同步系统的第二个办法就是引入故障检测器,进程可以认为在超过一定时间没有响应的进程已经故障。一种很常见的故障检测器的实现:超时(timeout)。
但是,这种办法要求故障检测器是精确的。如果故障器不精确的话,系统可能放弃一个正常的进程;如果超时时间设定得很长,进程就需要等待(并且不能执行任何工作)较长的时间才能得出出错的结论。这个方法甚至有可能导致网络分区。
解决办法是使用“不完美”的故障检测器。Chanadra 和 Toueg 在 "The weakest failure detector for solving consensus[7]" 中分析了一个故障检测器必须拥有的两个属性:
•完全性(Completeness):每一个故障的进程都会被每一个正确的进程怀疑。•精确性(Accuracy):正确的进程没有被怀疑。
同时,他们还证明了,即使是使用不可靠的故障检测器,只要通信可靠,崩溃的进程不超过 N/2,那么共识问题是可以解决的。我们不需要实现 Strong Completeness 和 Strong Accuracy,只需要一个最终弱故障检测器(eventually weakly failure detector),该检测器具有如下性质:
•最终弱完全性(eventually weakly complete):每一个错误进程最终常常被一些正确进程怀疑;•最终弱精确性(eventually weakly accurate):经过某个时刻后,至少一个正确的进程从来没有被其它正确进程怀疑。
该论文还证明了,在异步系统中,我们不能只依靠消息来实现一个最终弱故障检测器。但是,实际的故障检测器能够根据观察到的响应时间调节它的超时值。如果一个进程或者一个到检测器的连接很慢,那么超时值就会增加,那么错误地怀疑一个进程的情况将变得很少。从实用目的来看,这样的弱故障检测器与理想的最终弱故障检测器十分接近。
3、使用随机性算法(Non-Determinism)
这种解决不可能性的技术是引入一个随机算法,随机算法的输出不仅取决于外部的输入,还取决于执行过程中的随机概率。因此,给定两个完全相同的输入,该算法可能会输出两个不同的值。随机性算法使得“敌人”不能有效地阻碍达成共识。
和传统选出领导、节点再协作的模式不同,像区块链这类共识是基于哪个节点最快计算出难题来达成的。区块链中每一个新区块都由本轮最快计算出数学难题的节点添加,整个分布式网络持续不断地建设这条有时间戳的区块链,而承载了最多计算量的区块链正是达成了共识的主链(即累积计算难度最大)。
比特币使用了 PoW(Proof of Work)来维持共识,一些其它加密货币(如 DASH、NEO)使用 PoS(Proof of Stake),还有一些(如 Ripple)使用分布式账本(ledger)。
但是,这些随机性算法都无法严格满足安全性(safety)。攻击者可以囤积巨量算力,从而控制或影响网络的大量正常节点,例如控制 50% 以上网络算力即可以对 PoW 发起女巫攻击(Sybil Attack)[8]。只不过前提是攻击者需要付出一大笔资金来囤积算力,实际中这种风险性很低,如果有这么强的算力还不如直接挖矿赚取收益。
同步系统中的共识
上述的方法 1 和 2,都想办法让系统比较“同步”。我们熟知的 Paxos 在异步系统中,由于活锁的存在,并没有完全解决共识问题(liveness不满足)。但 Paxos 被广泛应用在各种分布式系统中,就是因为在达成共识之前,系统并没有那么“异步”,还是有极大概率达成共识的。
Dolev 和 Strong 在论文 "Authenticated Algorithms for Byzantine Agreement[9]" 中证明了:同步系统中,如果 N 个进程中最多有 f 个会出现崩溃故障,那么经过 f + 1 轮消息传递后即可达成共识。
Fischer 和 Lynch 的论文 "A lower bound for the time to assure interactive consistency[10]" 证明了,该结论同样适用于拜占庭故障。
基于此,大多数实际应用都依赖于同步系统或部分同步系统的假设。
同步系统中的拜占庭将军问题
Leslie Lamport、Robert Shostak 和 Marshall Pease 在 "拜占庭将军问题(The Byzantine General’s Problem)[11]" 论文中讨论了 3 个进程互相发送未签名(口头的)的消息,并证明了只要有一个进程出现故障,就无法满足拜占庭将军的条件。但如果使用签名的消息,那么 3 个将军中有一个出现故障,也能实现拜占庭共识。
Pease 将这种情况推广到了 N 个进程,也就是在一个有 f 个拜占庭故障节点的系统中,必须总共至少有 3f + 1 个节点才能够达成共识。即 N >= 3f + 1。
虽然同步系统下拜占庭将军问题的确存在解,但是代价很高,需要 O(N^f+1 ) 的信息交换量,只有在那些安全威胁很严重的地方使用(例如:航天工业)。
PBFT 算法
PBFT(Practical Byzantine Fault Tolerance)[12] 算法顾名思义是一种实用的拜占庭容错算法,由 Miguel Castro 和 Barbara Liskov 发表于 1999 年。
算法的主要细节不再展开。PBFT 也是通过使用同步假设保证活性来绕过 FLP 不可能。PBFT 算法容错数量同样也是 N >= 3f + 1,但只需要 O(n^2 ) 信息交换量,即每台计算机都需要与网络中其他所有计算机通讯。
虽然 PBFT 已经有了一定的改进,但在大量参与者的场景还是不够实用,不过在拜占庭容错上已经作出很重要的突破,一些重要的思想也被后面的共识算法所借鉴。
结语
本文参考了很多资料文献,对“共识问题”的研究历史做一些基础概述,希望能对你带来一点帮助。
本文提到的论文,很多直接谈论结果,忽略了其中的数学证明,一是本文只是提纲挈领的讨论共识问题,建立一个知识框架,后续方便往里面填充内容;二是考虑到大部分读者对数学证明过程并不敢兴趣,也不想本文变成一本书那么长。本文也遗漏许多重要算法,后续如有必要会继续补充。
限于本人能力,恳请读者们对本文存在的错误和不足之处,欢迎留言或私信告诉我。
下篇我们将会讨论 Paxos 算法。
References
[1] 第一篇提到共识问题的文献: http://betathoughts.blogspot.com/2007/06/brief-history-of-consensus-2pc-and.html[2] Time, Clocks and the Ordering of Events in a Distributed System: http://research.microsoft.com/users/lamport/pubs/time-clocks.pdf[3] Raft 的论文: https://www.usenix.org/system/files/conference/atc14/atc14-paper-ongaro.pdf[4] Byzantine failures: https://en.wikipedia.org/wiki/Byzantine_fault[5] Impossibility of Distributed Consensus with One Faulty Process: https://groups.csail.mit.edu/tds/papers/Lynch/jacm85.pdf[6] 《分布式系统:概念与设计》: https://book.douban.com/subject/21624776/[7] The weakest failure detector for solving consensus: https://dl.acm.org/doi/10.1145/234533.234549[8] 女巫攻击(Sybil Attack): https://en.wikipedia.org/wiki/Sybil_attack[9] Authenticated Algorithms for Byzantine Agreement: https://epubs.siam.org/doi/abs/10.1137/0212045?journalCode=smjcat[10] A lower bound for the time to assure interactive consistency: https://www.sciencedirect.com/science/article/abs/pii/0020019082900333[11] 拜占庭将军问题(The Byzantine General’s Problem): http://people.cs.uchicago.edu/~shanlu/teaching/33100_wi15/papers/byz.pdf[12] PBFT(Practical Byzantine Fault Tolerance): http://pmg.csail.mit.edu/papers/osdi99.pdf
推荐阅读
站长 polarisxu
自己的原创文章
不限于 Go 技术
职场和创业经验
Go语言中文网
每天为你
分享 Go 知识
Go爱好者值得关注
