伯克利团队重磅论文:神经网络没有免费午餐
大数据文摘授权转载自数据实战派
作者:刘媛媛
虽然我们还缺乏对机器智能基本理论的理解,但机器学习研究仍然以疯狂的速度推进。
现在的大多数机器学习论文,都专注于推进不同领域的新技术和新方法,例如自然语言处理和计算机视觉。
机器学习中的一些主要问题仍未得到解答,比如如何理解神经网络是怎么进行学习的?如何去量化知识泛化?
对此,不断有研究者提出一些新的想法来挑战以往对 ML 基础理论的常规理解。伯克利人工智能研究所(BAIR)最近发表的一篇开创性论文 Neural Tangent Kernel Eigenvalues Accurately Predict Generalization 是其中一个重要尝试(“数据实战派”后台回复“DL”可获得论文地址)。
该论文提出了一种新的泛化理论。
对泛化的理解仍然是现代机器学习中最大的谜团之一。为什么神经网络学习的函数可以很好地泛化到看不见的数据?从经典 ML 的角度来看,神经网络的高性能令人惊讶,因为它们被过度参数化,以至于它们可以很容易地表示无数泛化能力差的函数。
团队转而考虑以下定量问题:给定网络架构、目标函数和n个随机示例的训练集,能否有效地预测网络学习函数 的泛化性能?与之相应的理论不仅可以解释为什么神经网络可以很好地概括某些函数,而且还可以告诉我们给定架构非常适合哪些函数类,甚至可能让我们从第一原则中为给定问题选择最佳架构,如以及作为解决一系列其他深度学习之谜的通用框架。
事实证明这是可能的。
在 BAIR 最近的论文中,他们推导出了一个第一性原理理论,它允许人们对神经网络泛化做出准确的预测(至少在某些情况下)。
BAIR 研究人员在他们的论文中解决了以下陈述中所描述的泛化基本问题的变体:
如果提供给定数量的训练示例,是否可以根据第一原理有效地预测给定网络架构在学习给定函数时的泛化能力?
BAIR 团队依赖于最近在深度学习方面取得的两项突破来回答这个问题:
1)无限宽度网络
第一个突破是近年来深度学习发展的最有趣的理论之一——无限宽度网络理论,该理论表明:由于神经网络中的隐藏层趋向于无限,因此神经网络本身的行为采用非常简单的分析形式。这个想法表明,通过研究理论上的无限神经网络,可以深入了解有限等价物的泛化。这点类似于传统微积分中的中心极限定理。
2)核回归近似
第二个突破与第一个突破密切相关,但更具体。深度学习泛化的最新研究表明,利用梯度下降法训练一个具有均方误差(MSE)损失函数的宽网络等效于被称为核回归的经典模型。在这种情况下,核代表网络的“神经切线内核”(NTK),它描述了使用梯度下降训练时的演化过程。研究表明核回归(以 NTK 为内核)的 MSE 近似值可以准确预测网络学习任意函数的 MSE。
这项研究中,BAIR 提出的泛化性第一原理最大的贡献是可学习性的概念。
可学习性的思想是量化目标函数和学习函数之间的近似值。这听起来与 MSE 相似,但可学习性表现出与 MSE 完全不同的特性,这使得它更适合后续的模型。
在下图中,展示了用不同的训练大小去训练四种不同神经网络(不同颜色分别代表不同神经网络)的结果。曲线代表理论预测,点代表真实性能。我们可以看到可学习性指标的一致性要好很多。
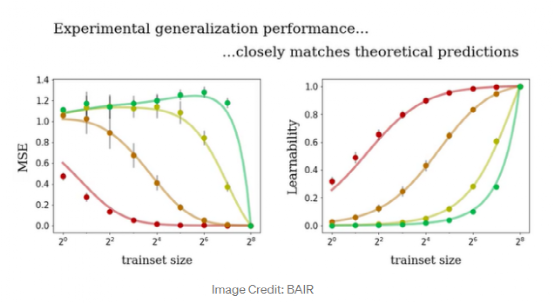
BAIR 研究的结果远非结论性的,而表明了尽管神经网络在难以捉摸这个特质上“臭名昭著”,但人们仍然希望了解它们何时以及为何能正常工作。
就像在其他科学领域一样,人们仍然可以找到简单的规则来管理这些看似复杂的系统。在真正理解深度学习之前,还有更多的工作要做,比如该理论只适用于 MSE 损失,除了最简单的情况之外,NTK 特征系统在所有情况下都是未知的。