印度天才数学家拉马努金留下的3000+神奇公式，交给AI来「证明」！

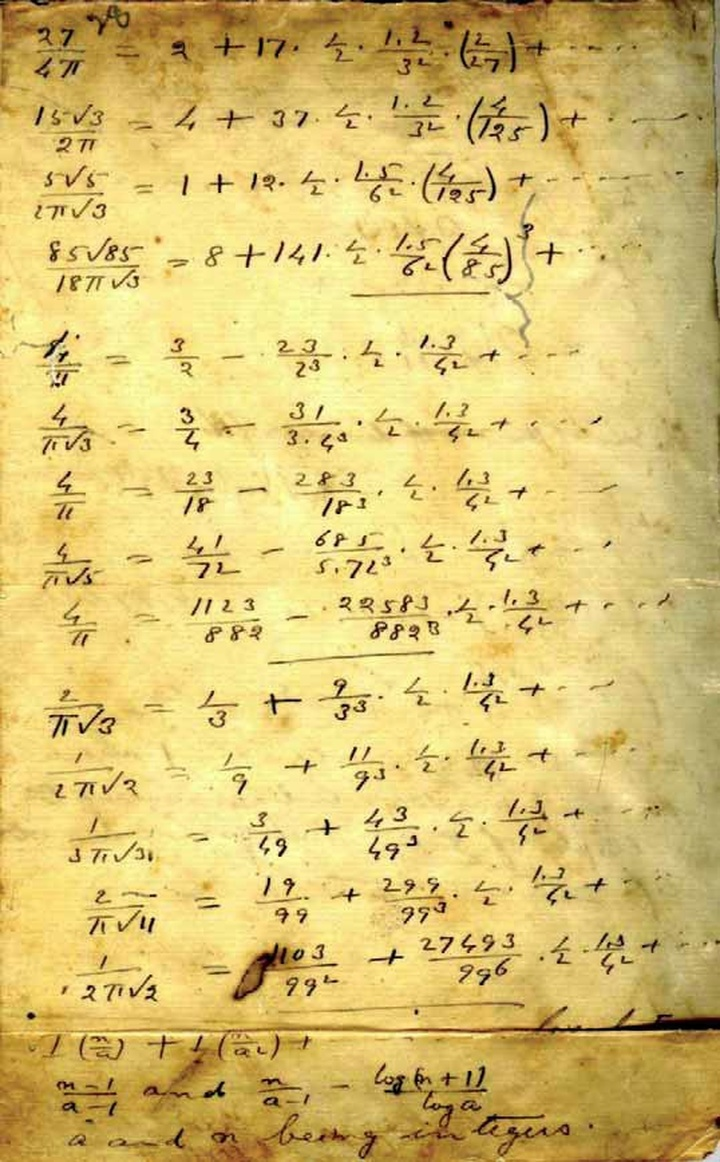
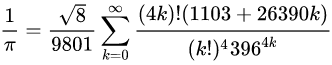
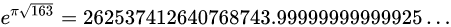
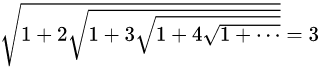
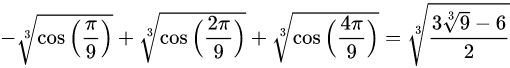
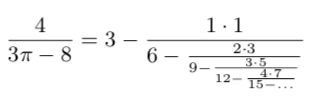
像 e 和 π 这样的基本常数在不同的科学领域无处不在，包括物理学、生物学、化学、几何学和抽象数学。然而，几个世纪以来，与基本常数有关的新的数学公式很少，而且通常是凭借数学直觉或创造力偶尔发现的。

Ramanujan 机器可以从众所周知的公式开始计算数字，例如 π 的前几千位数字。从这些数据中，该算法试图预测一个新的表达式，这个表达也可以做同样的计算得到相同的结果。

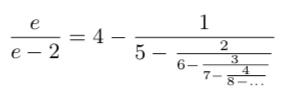
这个过程会产生一个很好的猜测（conjecture），然后就要靠人类数学家来证明这个表达式是否能够正确地计算出整个数字。

该团队在2019年开始就在该项目的网站上公开这些推测，研究人员已经证明了其中的一些猜测是正确的。

但有些问题仍有待解决，其中一个是关于 「Apery 常数」的问题，Apery 常数在物理学中有重要应用。「最后一个结果，也是最令人兴奋的一个，但是没有人知道如何证明」，物理学家 Ido Kaminer 说，「但是算法自动创造的推测可以指引数学家们找到人们不知道存在的数学分支之间的联系」。

连分数（Continued fractions）

拉马努金机器目前的应用还十分有限: 到目前为止，算法只能生成一个特定类型的式子，称为连分数。这些分数表示一个数字为一个无限的分数序列，这些分数嵌套在彼此的分母中。

团队人员已经尝试了一系列算法来寻找连分数，并将它们应用到各种概念上重要的数字上。其中一个是加泰罗尼亚常数（Catalan’s constant），这个数字起源于十九世纪比利时数学家欧仁 · 加泰罗尼亚的研究。

加泰罗尼亚常数大约为0.916，但它是如此神秘，以至于没有人知道它是否是有理的，也就是说它是否可以表示为两个整数的分数。

数学家们能做的最好的事情就是证明它的「非理性指数」——用有理数来近似一个数字的难度的度量，这个值至少是0.554。证明加泰罗尼亚常数是无理的等价于证明其非理性指数大于1。而由拉马努金机器生成的公式，使卡米纳的团队在最好的人类结果上略有改善，使指数达到0.567。

自动生成猜测并不是计算机帮助推动数学发展的唯一领域。

计算机辅助计算在几个引人注目的结果的证明中发挥了关键作用。最近，一些数学家在人工智能方面取得了进展，人工智能不仅能进行重复的计算，还能自己做出证明。另一个正在发展的领域是软件，它可以检查人类写的数学证明，并检查它是否正确。

「最终，人类将会被淘汰」，Zeilberger 说，他是证明自动化领域的先驱，并且帮助证实了 Ramanujan 机器的一些猜想，「随着人工智能产生的数学的复杂性增加，数学家们将只能粗略地理解计算」，他补充道。

不过，尽管计算机可能能够提出数学陈述，甚至证明它们是正确的，但是如果没有人类的干预，目前还不清楚它们是否能够区分深刻的，有趣的陈述，还是仅仅从技术上是正确的而已。

如果感兴趣的话，你可以在下面的链接中运行 Ramanujan 算法来发现新的数学猜想，如果能够证明是正确的，那么发现的新猜想将以你的名字命名！

参考链接：

http://www.ramanujanmachine.com/

Github项目链接：

https://github.com/AnonGit90210/RamanujanMachine