漫画:如何螺旋遍历二维数组?


————— 第二天 —————



什么意思呢?我们来举个例子,给定下面这样一个二维数组:

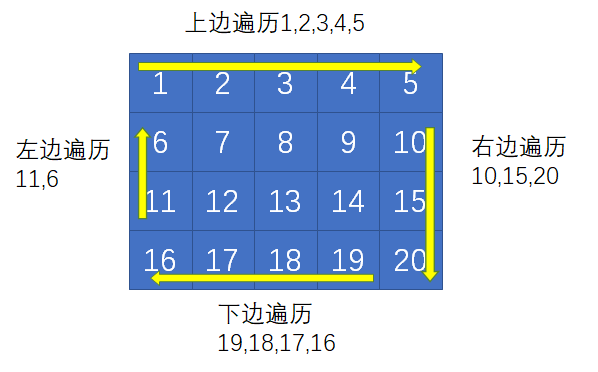
我们需要从左上角的元素1开始,按照顺时针进行螺旋遍历,一直遍历完所有的元素,遍历的路径就像下图一样:
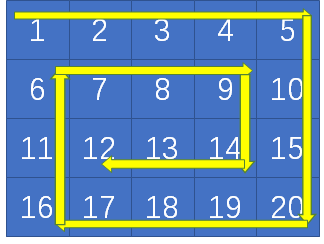
经过这样的遍历,返回的元素结果如下:
1,2,3,4,5,10,15,20,19,18,17,16,11,6,7,8,9,14,13,12




————————————






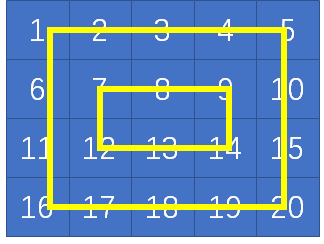


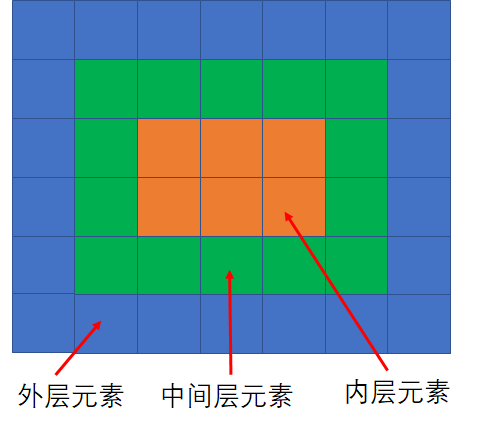

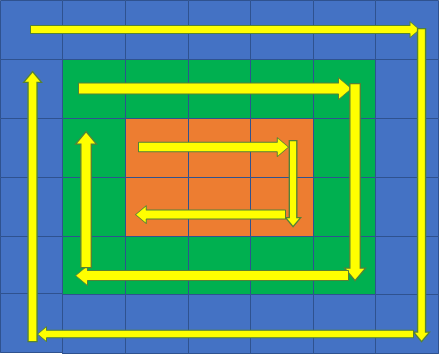



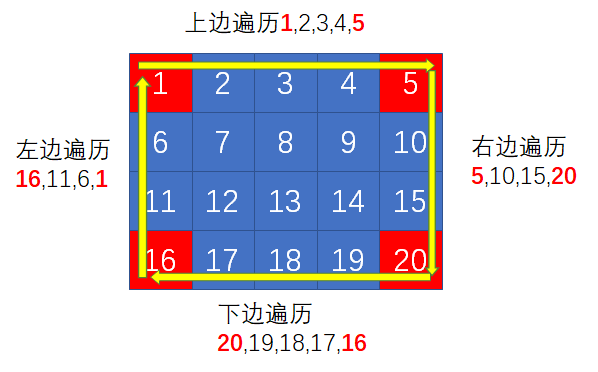
第1层
从左到右遍历“上边”:
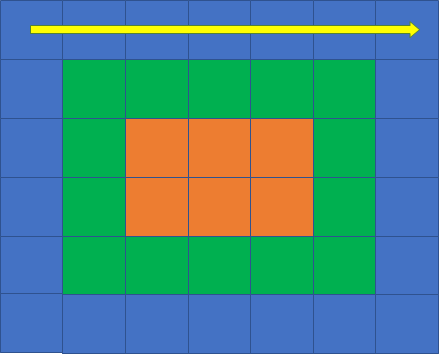
从上到下遍历“右边”:
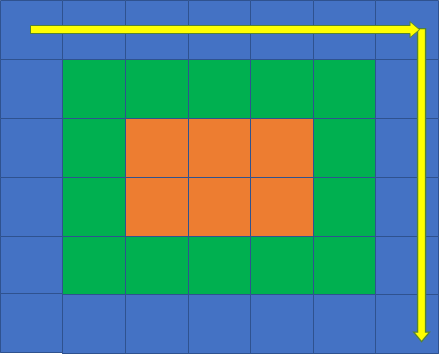
从右到左遍历“下边”:
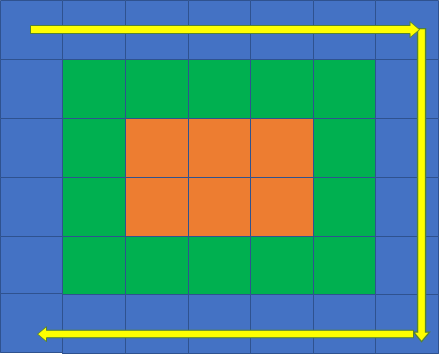
从下到上遍历“左边”:
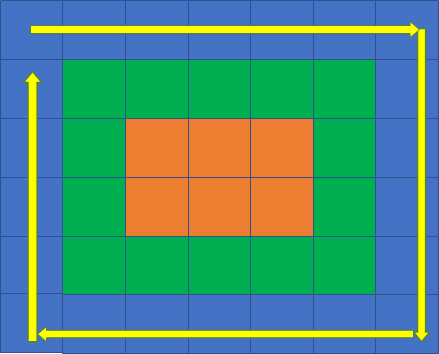
第2层
从左到右遍历“上边”:
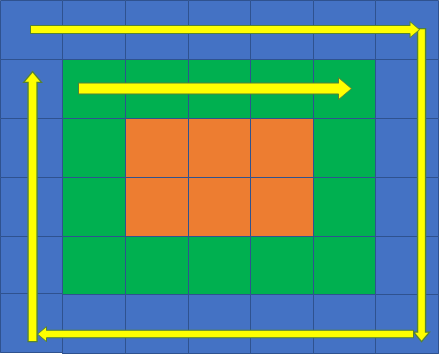
从上到下遍历“右边”:
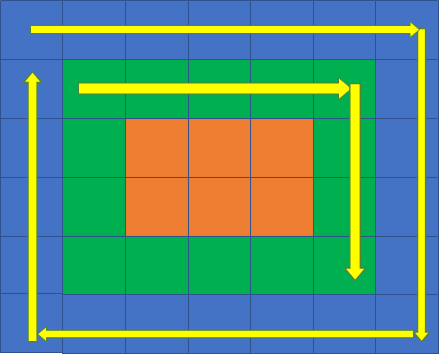
从右到左遍历“下边”:
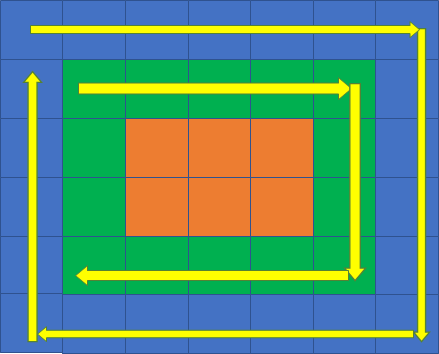
从下到上遍历“左边”:
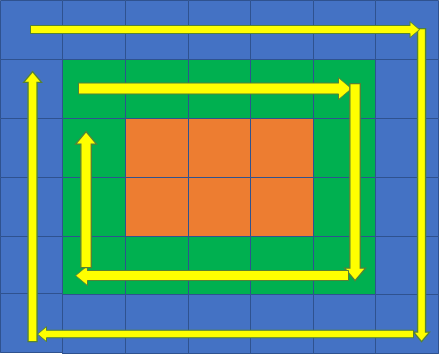
第3层
从左到右遍历“上边”:
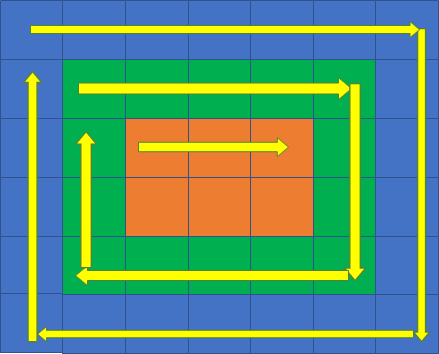
从上到下遍历“右边”:
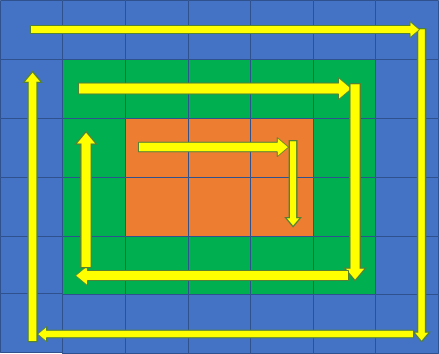
从右到左遍历“下边”:
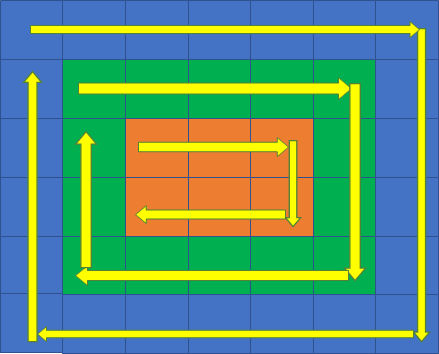
第三层的“左边”已无需遍历,二维数组到此遍历完毕。





public class SpiralOrder {
public static List spiralOrder(int[][] matrix) {
List list = new ArrayList();
//当二维数组是空或任何一个维度是0,直接返回
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return list;
}
//m是矩阵的行数
int m = matrix.length;
//n是矩阵的列数
int n = matrix[0].length;
//大循环,从外向内逐层遍历矩阵
for(int i=0; i<(Math.min(m, n)+1)/2; i++) {
//从左到右遍历“上边”
for (int j=i; j list.add(matrix[i][j]);
}
//从上到下遍历“右边”
for (int j=i+1; j list.add(matrix[j][(n-1)-i]);
}
//从右到左遍历“下边”
for (int j=i+1; j list.add(matrix[(m-1)-i][(n-1)-j]);
}
//从下到上遍历“左边”
for (int j=i+1; j1-i; j++) {
list.add(matrix[(m-1)-j][i]);
}
}
return list;
}
public static void main(String[] args) {
int[][] matrix = {
{ 1, 2, 3, 4, 5 },
{ 6, 7, 8, 9, 10 },
{ 11, 12, 13, 14, 15 },
{ 16, 17, 18, 19, 20 }
};
int[][] matrix2 = {
{ 1, 2, 3, 4, 5 },
{ 6, 7, 8, 9, 10 },
{ 11, 12, 13, 14, 15 },
{ 16, 17, 18, 19, 20 },
{ 21, 22, 23, 24, 25 }
};
List resultList1 = spiralOrder(matrix);
System.out.println(Arrays.toString(resultList1.toArray()));
List resultList2 = spiralOrder(matrix2);
System.out.println(Arrays.toString(resultList2.toArray()));
}
}
在上面的代码中,一个大循环当中包含了4个小循环。大循环控制了每一层的遍历,4个小循环分别实现了同一层上边、右边、下边,左边的遍历。
当遍历到最内层时,4个小循环并不会全都执行,比如测试代码中matrix2的最内层只有一个元素13,那么执行完第1个小循环,就不会再进入后面3个小循环:




—————END—————
扫码关注公众号,订阅更多精彩内容。
评论
