程序员学数学读哪本书?(文末赠送精美礼品)

在互联网一直流传了一个这样的段子——
“一流程序员靠数学,二流靠算法,三流靠逻辑,四流靠SDK,五流靠Google和StackOverFlow,六流靠百度和CSDN。低端的看高端的就是黑魔法!”
虽然是段子,但其实也挺写实的,因为你打开各大招聘网站,会发现越是高薪的IT岗位,对数学的要求越高。其实,我曾经也不太明白数学为什么对程序员很重要,不明白为什么在大学里初入编程之门时,老师却要求你去看《数学之美》。
但后来,我有幸阅读了计算机大佬黄申写的《程序员的数学基础课 从理论到Python实践》一书,才意识到数学对于程序员的重要性。

作者:黄申
正如他在书写道:“数学对我们每一个程序员来说,都是最熟悉的陌生人。你从小就开始学习数学,那些熟悉的数学定理和公式陪伴你走过好多年。但是,自从当了程序员,你可能早就将数学抛在了脑后。 毕竟,作为一个基础学科,数学肯定没有操作系统、数据结构、计算机网络这样的课程看起来 “实用”。
上大学的时候,我非常喜欢编程,不喜欢待在教室里听数学老师讲那些枯燥的数学理论和定理。再到后来,我读了硕士和博士,开始接触更多的算法和机器学习,猛然间才发现机器学习表面上是“写程序”,剥去外表,本质上是在研究数学。”
数学不仅仅是程序员的工具,更是从低端向高端进阶的黑魔法。那么如何学好数学给自己夯实好进阶的台阶呢?在《程序员的数学基础课 从理论到Python实践》这本书中,你一定可以找到答案!
程序员的数学思维很重要!
在V2EX论坛上有一个帖子一直挂着一个帖子,这个帖子的问题是“数学对程序员来说真的很重要吗?”这个帖子下经常有人来更新,回答的内容几乎都是说数学对于程序员来说十分重要。

其中,有一位网友的回答令我记忆尤深。

“懂数学的才能叫程序员,不懂的只能停留在码农级别,这不是说你编码用不用数学,数学本身就是逻辑思维的能力。”这个回答说得太好了!不仅一针见血地指出了程序员之间出现的等级差距,还进一步揭示了造成这种差距的原因——缺乏数学思维。
显而易见,程序员如果缺乏数学思维会使自己处于劣处,造成天平的失衡。
正如本书中,以作者黄申多年的工作经历来看,数学学得好不好将会直接决定一个程序员有没有发展潜力。往大了说,数学是一种思维模式,考验的是一个人归纳、总结和抽象的能力。
将这个能力放到程序员的世界里,其实就是解决问题的能力。往小了说,不管是数据结构与算法还是程序设计,其实底层很多原理或者思路都源自数学,所以很多大公司在招人时也会优先考虑数学专业的毕业生,因为这些人的数学基础很好,学起编程来也容易上手。
如果编程语言是血肉,那么数学的思想和知识就是灵魂。它可以帮助你选择合适的数据结 构和算法,提升系统效率,并且赋予机器智慧。在大数据和智能化的时代更是如此。
总而言之,数学决定了一个人技术上能发展的上限,它对程序员来说意义非凡!
程序员学数学需要掌握的基础思想
既然程序员的数学思维如此重要,那么程序员学数学需要掌握哪些基础思想呢?
二进制
二进制(binary)在数学和数字电路中指以2为基数的记数系统,以2为基数代表系统是二进位制的。这一系统中,通常用两个不同的数字0和1来表示。
二进制是计算机系统的基础,数字电子电路中,逻辑门直接采用了二进制,因此现代的计算机和依赖计算机的设备里都用到二进制。每个数字称为一个比特(Bit,Binary digit 的缩写)。
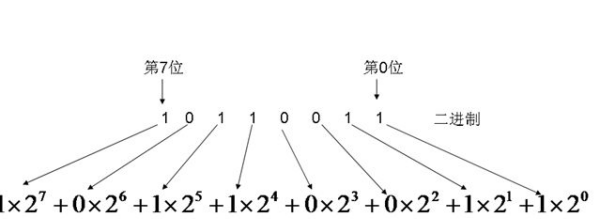
(二进制)
余数
余数就是指整数除法中被除数未被除尽的部分,且余数的取值范围为 0 到除数之间(不包括除数自身)。取余数运算 a mod b = c(b不为0)表示整数a除以整数b所得余数为c。例如:32÷5= 6…2,更专业的符号也可以写作 32÷5=6 又 2/5,或者32 mod 5=2。
可不要小看余数,无论是在日常生活中,还是计算机领域中,它都发挥着重要的作用。当然,计算机中的余数思想大多被运用在很多常见的算法和数据结构中,而且有可能你在不知情情况下就运用到它。
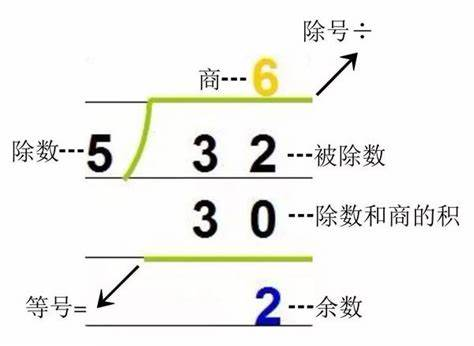
(求余数)
布尔代数
布尔代数是一个用于集合运算和逻辑运算的公式:〈B,∨,∧,¬ 〉。其中B为一个非空集合,∨,∧为定义在B上的两个二元运算,¬为定义在B上的一个一元运算。通过布尔代数进行集合运算可以获取到不同集合之间的交集、并集或补集,进行逻辑运算可以对不同集合进行与、或、非。
可以说,布尔代数算是编程中控制逻辑的灵魂。因为真值可以在逻辑电路中表示为二进制数数或电平,这种相似性同样扩展到它们,所以布尔代数在电子工程和计算机科学中同在数理逻辑中一样有很多实践应用。在电子工程领域专门化了的布尔代数也叫做逻辑代数,在计算机科学领域专门化了布尔代数也叫做布尔逻辑。
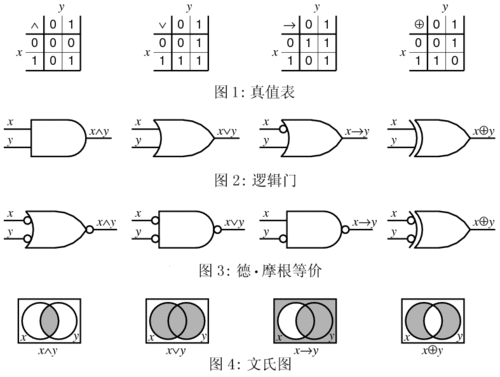
(布尔代数)
迭代
迭代是重复反馈过程的活动,其目的通常是为了接近并到达所需的目标或结果。每一次对过程的重复被称为一次“迭代”,而每一次迭代得到的结果会被用来作为下一次迭代的初始值。
数学中的迭代可以指函数迭代的过程,即反复地运用同一函数计算,前一次迭代得到的结果被用于作为下一次迭代的输入。
在计算机科学中,迭代是程序中对一组指令(或一定步骤)的重复。它既可以被用作通用的术语(与“重复”同义),也可以用来描述一种特定形式的具有可变状态的重复。
将迭代法和计算机强大的处理能力相结合,我们能创造出很有价值的数据结构和算法。

(一个五边形的迭代。将对角用直线段连起来得到一个五角星,后者中心围成了一个倒过来的小五边形。迭代地执行这一过程会产生一系列嵌套的五边形和五角星。)
递归
递归(Recursion),在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。例如,当两面镜子相互之间近似平行时,镜中嵌套的图像是以无限递归的形式出现的。也可以理解为自我复制的过程。
程序调用自身的编程技巧称为递归。递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。

(德罗斯特效应是递归的一种视觉形式。图中女性手持的物体中有一幅她本人手持同一物体的小图片,进而小图片中还有更小的一幅她手持同一物体的图片,依此类推。)
数学归纳法
数学归纳法(Mathematical Induction、MI、ID)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。

(多米诺骨牌效应:骨牌一个接一个倒下,
就如同一个值到下一个值的过程)
迭代和递归,以及与它们相关的数学归纳,是和基础编程关系非常紧密的。迭代法和递归都是通过不断反复的步骤,计算数值或进行操作的方法。迭代一般适合正向思维,而递归一般适合逆向思维。而递归回溯的时候,也体现了正向递推的思维。它们本身都是抽象的流程,可以由不同的编程实现。
排列和组合
排列(permutation),一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列。特别地,当m=n时,这个排列被称作全排列(all permutation)。
组合(combination),是一个数学名词。一般地,从n个不同的元素中,任取m(m≤n)个元素为一组,叫作从n个不同元素中取出m个元素的一个组合。我们把有关求组合的个数的问题叫作组合问题。
动态规划
动态规划(Dynamic Programming,DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法,是求解决策过程最优化的过程。
20世纪50年代初,美国数学家贝尔曼等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划能减少不必要的排列 和组合,最终大幅提升算法的性能。
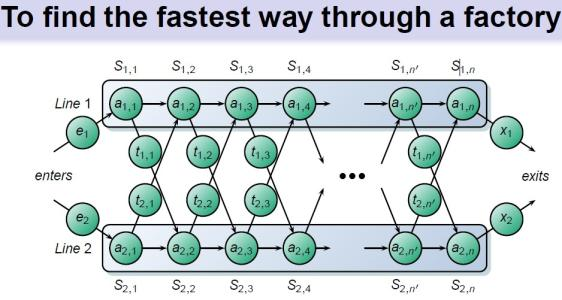
(算法中的动态规划问题)
树
树是图论中最重要的概念之一,也是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
它具有以下的特点:每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树。
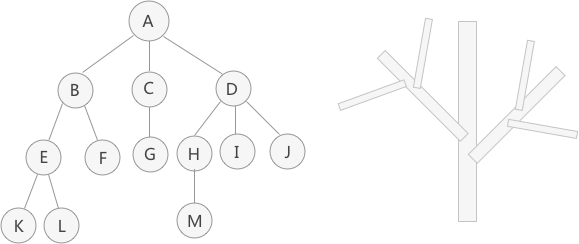
(数据结构中的树存储结构)
图
在数学的分支图论中,图(Graph)用于表示物件与物件之间的关系,是图论的基本研究对象。一张图由一些小圆点(称为顶点或结点)和连结这些圆点的直线或曲线(称为边)组成。
图是一种多对多的数据结构,比线性表和树更复杂,它由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
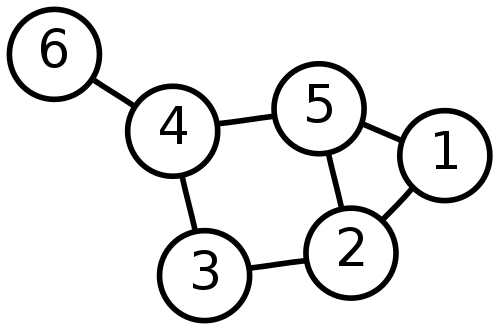
(一个有六个顶点,七个边的图)
......
《程序员的数学基础课》如何能帮你搞定数学?
可能有的人看到上面那些数学的基础思想,就开始感到烦躁。
毕竟数学是个博大精深的学科,有些数学名词光是耳闻或目睹就开始令人撤退,但我们的目标不是成为数学集大成者,只要学好程序员所需要的数学,就足以培养好数学思维,逐步跨越等级鸿沟。
为此,本书的作者黄申也在书中,循序渐进,巧立重点——“程序员需要学的数学知识”,让数学变得更加容易学习,程序员们也更快理解数学思维。
首先,他梳理了编程中常用的数学概念, 由浅入深剖析它们的本质,希望能够帮程序员读者彻底掌握这些基础、核心的数学知识。这其中包括那些曾经熟悉的数学名词,如数学归纳法、迭代法、递归、排列、组合等。
其次,他将线性代数和概率统计中的抽象概念、公式、定理都由内而外地讲了出来,并分析它们在编程中的应用案例,帮助程序员读者提升编程的高阶能力。对于这些内容,他从基本的概念入手,结合生活和工作中的实际案例,让程序员读者更轻松地理解概念的含义。
按照这样的讲解路线,既能让程序员读者巩固基础的概念和知识,同时又能让他们明白这些基础性的内容,对计算机编程和算法究竟意味着什么。
总而言之,这本书的内容从概念到应用,再到本质,层层深入,不但注重培养读者养成良好的数学思维,而且努力使读者的编程技术实现进阶,非常适合希望从本质上提升编程质量的中级程序员阅读和学习。
值得一提的是,这本书的作者黄申之前在网站上开过一堂以本书内容为主的课程,赢得好声一片。网友们纷纷评论:
“希望大神能带我入门!”
“工作几年,越来越觉得数学重要”
“在游戏领域做了8年了,越来越觉得数学的重要。“
“希望我那浅薄的数学底子能跟得上,坚持坚持!"
“希望自己能学到点,数学虐我千百遍,我待数学如初恋!”
“自己在学习算法与数据结构时,就遇到了基本的数学思想与计算公式,来计算时间复杂度。需要从新拿起数学,正想着看视频学习高数,但学的又太多与编程无关的知识,太浪费时间,这样的专栏果断下单,跟着大神学习,提高效率,降低成本,时间太重要!”
“第一时间购买,数据结构和算法很重要,但是很多算法又离不开数学!”
“已经迫不及待了!”
......
而其中,也有一位读者的留言让我颇为感动:

“可能我一辈子也没法成为顶级程序员,可我现在就想开始改变了。”再渺小的人物也有远大的志向,不论我们身处程序员哪一等级,只要我们心中有光,并为之努力奋斗,便都是顶级人才!就让这本程序员补数学的绝佳伴侣《程序员的数学基础课 从理论到Python实践》陪伴着我们一同前行,创造黑魔法,成为优秀的程序魔导师吧!
加油!相信自己!

(图灵奖)

作者:黄申
1.紧紧围绕程序员的需求。
数学的课题非常广泛,但本书没有涉及数学领域的全部课题,而是从程序员的需求出发,精心挑选了编程所需的常用知识点,并实现学以致用。
2.结合生动的案例和形象的比喻解读难点。
降低技术理解的门槛,让程序员更容易理解数学背后的逻辑,并对实际生产问题进行数学建模,进而设计出更有效的算法,编写出更优雅的代码。
3.注重编程实践。
除了阐述理论知识,书中还提供了要通过大量实践才能积累的宝贵经验,让读者有机会亲自动手编写Python 代码,进而加深理解。
4.提供源代码下载。
参考来源: