poj 1034 The dog task

The dog task

Description

Hunter Bob often walks with his dog Ralph. Bob walks with a constant speed and his route is a polygonal line (possibly self-intersecting) whose vertices are specified by N pairs of integers (Xi, Yi) ? their Cartesian coordinates.

Ralph walks on his own way but always meets his master at the specified N points. The dog starts his journey simultaneously with Bob at the point (X1, Y1) and finishes it also simultaneously with Bob at the point (XN, YN).
Ralph can travel at a speed that is up to two times greater than his master's speed. While Bob travels in a straight line from one point to another the cheerful dog seeks trees, bushes, hummocks and all other kinds of interesting places of the local landscape which are specified by M pairs of integers (Xj',Yj'). However, after leaving his master at the point (Xi, Yi) (where 1 <= i < N) the dog visits at most one interesting place before meeting his master again at the point (Xi+1, Yi+1).
Your task is to find the dog's route, which meets the above requirements and allows him to visit the maximal possible number of interesting places. The answer should be presented as a polygonal line that represents Ralph's route. The vertices of this route should be all points (Xi, Yi) and the maximal number of interesting places (Xj',Yj'). The latter should be visited (i.e. listed in the route description) at most once.
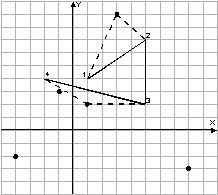
An example of Bob's route (solid line), a set of interesting places (dots) and one of the best Ralph's routes (dotted line) are presented in the following picture:

Input

The first line of the input contains two integers N and M, separated by a space ( 2 <= N <= 100 ,0 <= M <=100 ). The second line contains N pairs of integers X1, Y1, ..., XN, YN, separated by spaces, that represent Bob's route. The third line contains M pairs of integers X1',Y1',...,XM',YM', separated by spaces, that represent interesting places.
All points in the input file are different and their coordinates are integers not greater than 1000 by the absolute value.

Output

The first line of the output should contain the single integer K ? the number of vertices of the best dog's route. The second line should contain K pairs of coordinates X1'',Y1'' , ...,Xk'',Yk'', separated by spaces, that represent this route. If there are several such routes, then you may write any of them.

Sample Input

4 5
1 4 5 7 5 2 -2 4
-4 -2 3 9 1 2 -1 3 8 -3

Sample Output

6
1 4 3 9 5 7 5 2 1 2 -2 4

狗的任务

描述

猎人鲍勃经常和他的狗拉尔夫一起散步。Bob 以恒定速度行走，他的路线是一条折线（可能自相交），其顶点由 N 对整数 (Xi, Yi) 指定？他们的笛卡尔坐标。

拉尔夫走自己的路，但总是在指定的 N 点遇到他的主人。狗与鲍勃在 (X1, Y1) 点同时开始他的旅程，并在 (XN, YN) 点与鲍勃同时结束。
拉尔夫可以以比主人速度高两倍的速度移动。当鲍勃从一个点直线移动到另一个点时，快乐的狗寻找树木、灌木、小丘和当地景观中所有其他类型的有趣地方，这些地方由 M 对整数 (Xj',Yj') 指定。然而，在点（Xi，Yi）（其中 1 <= i < N）离开他的主人后，狗最多访问一个有趣的地方，然后在点（Xi+1，Yi+1）再次见到他的主人。
你的任务是找到符合上述要求的狗的路线，并允许他访问尽可能多的有趣的地方。答案应显示为代表拉尔夫路线的折线。这条路线的顶点应该是所有点（Xi，Yi）和最大数量的有趣地点（Xj'，Yj'）。后者最多应该被访问一次（即在路线描述中列出）。
Bob 的路线示例（实线）、一组有趣的地方（点）和 Ralph 的最佳路线之一（虚线）如下图所示：

输入

输入的第一行包含两个整数 N 和 M，用空格分隔 ( 2 <= N <= 100 ,0 <= M <=100 )。第二行包含 N 对整数 X1, Y1, ..., XN, YN，用空格分隔，代表 Bob 的路线。第三行包含 M 对整数 X1',Y1',...,XM',YM'，用空格分隔，代表有趣的地方。
输入文件中的所有点都不同，它们的坐标是绝对值不大于 1000 的整数。

输出

输出的第一行应该包含单个整数 K ? 最佳狗路线的顶点数。第二行应该包含 K 对坐标 X1'',Y1'' , ...,Xk'',Yk''，用空格分隔，代表这条路线。如果有几个这样的路由，那么你可以写任何一个。

样本输入

4 5
1 4 5 7 5 2 -2 4
-4 -2 3 9 1 2 -1 3 8 -3

样本输出

6
1 4 3 9 5 7 5 2 1 2 -2 4

题意：Bob和他的狗一起溜达，狗移动的速度是Bob的2倍。先给出Bob行走路线上的一些点，

每次Bob从（x，y）走时狗可以离开他去玩耍或观赏一些景点，但要保证在Bob到达（x+1,y+1）时狗也达到了(x+1,y+1);

同时给出了一些景点的坐标。求小狗狗最多可以经过多少的已给的点（即Bob路线上的所有点+小狗走的景点），并把

小狗狗的行走路线打印出来

思路：简单的二分图求最大匹配问题，根据景点到（x,y）和（x+1,y+1）距离之和与（x,y）和（x+1,y+1）之间距离的2倍

关系建图，然后求解最大匹配即可

代码：

#include 
#include 
#include 
using namespace std;
const int MAX=110;
 
int n,m;
typedef struct node
{
    int x;
    int y;
} Node;
Node bob[MAX];
Node dog[MAX];
int g[MAX][MAX];
double getdis(Node a,Node b)
{
    return sqrt((double)(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int linker[MAX];
int save[MAX];
int used[MAX];
bool dfs(int u)
{
    for(int v=0; v    {
        if(g[u][v]&&!used[v])
        {
            used[v]=true;
            if(linker[v]==-1||dfs(linker[v]))
            {
                linker[v]=u;
 
                return true;
            }
        }
    }
    return false;
}
int hungary()
{
    int res=0;
    memset(linker,-1,sizeof(linker));
    for(int u=0; u    {
        memset(used,false,sizeof(used));
        if(dfs(u)) res++;
    }
    return res;
}
int main()
{

    scanf("%d%d",&n,&m);
    for(int i=0; i        scanf("%d%d",&bob[i].x,&bob[i].y);
    for(int i=0; i        scanf("%d%d",&dog[i].x,&dog[i].y);
    memset(g,0,sizeof(g));
    for(int i=0; i        for(int k=0; k        {
            double a=getdis(bob[i],bob[i+1]);
            double b=getdis(bob[i],dog[k]);
            double c=getdis(bob[i+1],dog[k]);
            if(b+c-a-a<10e-8)
                g[i][k]=1;
        }
    printf("%d\n",hungary()+n);
    memset(save,-1,sizeof(save));
    for(int i=0; i    {
        if(linker[i]!=-1)
            save[linker[i]]=i;
    }
    for(int i=0; i    {
        printf("%d %d ",bob[i].x,bob[i].y);
        if(save[i]!=-1)
            printf("%d %d ",dog[save[i]].x,dog[save[i]].y);
    }
    printf("%d %d\n",bob[n-1].x,bob[n-1].y);
    return 0;
}