博弈论之囚徒困境
来源：小浩算法
作者：程序员浩哥
本系列将为大家带来一整套的博弈论问题。因为在面试的过程中，除了常规的算法题目，我们经常也会被问到一些趣味题型来考察思维，而这类问题中，很多都有博弈论的影子存在。这些公司里以FLAG（Facebook, LinkedIn, Amazon, Google）为典型，特别喜欢考察本类题型。同时，本系列将不一定都是算法问题，不是IT行业的小伙伴也可以进行学习，来提高分析问题的能力~
古语有云，“笑人情似纸，世事如棋”。生活中每个人如同棋手，其每一个行为如同在一张看不见的棋盘上布子，精明慎重的棋手们相互揣摩、牵制、争赢，下出诸多精彩纷呈、变化多端的棋局。而什么是博弈论？就是研究棋手们 的“出棋” 过程，从中抽象出可逻辑化的部分，并将其系统化的一门科学，也是运筹学的一个重要学科。
我们从最简单的一道“囚徒困境”来进行学习~
囚徒困境：一件严重的纵火案发生后，警察在现场抓到两个犯罪嫌疑人。事实上，正是他们一起放火烧了这座仓库。但是，警方没有掌握足够的证据，只得把他们分开囚禁起来，要求他们坦白交代。在分开囚禁后，警察对其分别告知：
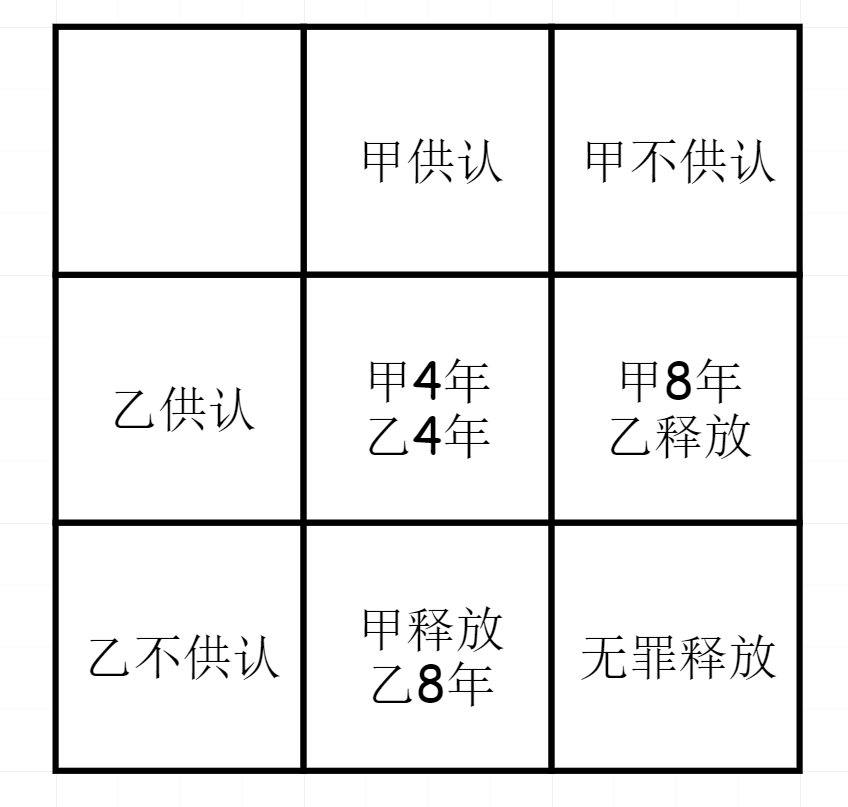
如果你坦白，而对方不坦白，则将你释放，判对方8年。
如果你不坦白，而对方坦白，则将对方释放，而判你8年。
如果你两都坦白了，则判你两各自4年。
那么两个囚犯应该如何做，是互相背叛还是一起合作？
从表面上看，其实囚犯最应该的就是一起合作，都不坦白，这样因为证据不足，会将两人都进行释放。但是！因为事实确实是两人放的火，所以他们不得不进行思考，另一人采取了什么样的行为？
犯人甲当然不傻，他根本无法相信同伙不会向警方提供任何信息！因为如果同伙一旦坦白，而自己这边如果什么都没说的话，就可以潇洒而去。但他同时也意识到，他的同伙也不傻，也会同样来这样设想他。
所以犯人甲的结论是，唯一理性的选择就是背叛同伙，把一切都告诉警方！这样的话，如果他的同伙笨得只会保持沉默，那么他就会是那个离开的人。而如果他的同伙也根据这个逻辑向警方交代了，那么也没有关系，起码他不必服最重的刑！
这场博弈的过程，显然不是顾及团体利益的最优解决方案。以全体利益而言，如果两个参与者都合作保持沉默，两人都可以无罪释放，总体利益更高！但根据假设（人性），二人均为理性的个人，且只追求自己的个人利益。均衡状况会是两个囚徒都选择背叛，这就是“困境”所在！
事实上，这种两人都选择坦白的策略以及因此被判4年的结局被称作“纳什均衡”（也叫非合作均衡），换言之，在此情况下，无一参与者可以“独自行动”（即单方面改变决定）而增加收获。
我们看一下官方释意是多么难懂“所谓纳什均衡，指的是参与人的一种策略组合，在该策略组合上，任何参与人单独改变策略都不会得到好处。”简单点讲，如果在一个策略组合上，当所有其他人都不改变策略时，没有人会改变自己的策略，则该策略组合就是一个纳什均衡。
推荐阅读