经典逻辑面试题,高楼扔鸡蛋

有一栋100层的楼,和2个坚硬的鸡蛋,从楼上扔下鸡蛋,鸡蛋会在大于某一层刚好开始碎,那最少几次能测出鸡蛋能承受的最大楼层呢?
如果从第50层扔下鸡蛋没碎,第51层扔下碎了,那鸡蛋能承受的最大楼层就是50。
注意:你手上只有2个鸡蛋,如果扔下碎了,就没法再使用了。
小明条件反射般作答,从1层开始往上测试,到第i层碎掉就有结果了。
小K说,这个方法确实可以测出来,但太慢了(当然暂不考虑下楼捡蛋的时间啦)。如果100层碎,最坏你得测试100次。如果先从第50层扔下呢?
这样分2种情况,碎和不碎:
碎:则还有1个蛋,再从1层开始逐层往上测试,最坏测到49层,总共50次。
不碎:则还有2个蛋,再从51层开始逐层往上测试,最坏测到100层,总共51次。
小明说,这个方法确实好一些,等等,你刚才说第2种情况是什么?
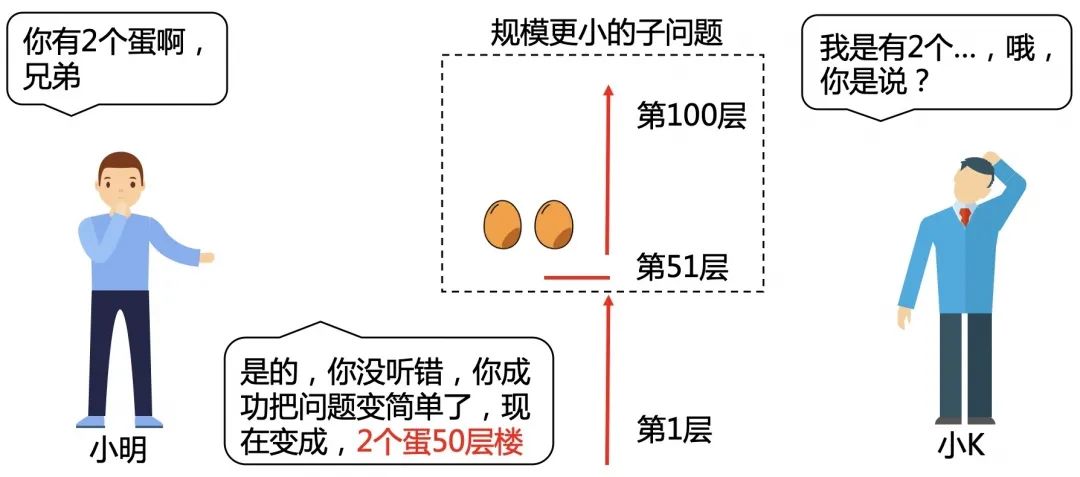
小明接着说,你还有2个蛋啊,兄弟,为啥不充分利用呢?
不考虑1-50层,可以把51-100层看成一栋新的楼,现在问题就变成用2个蛋测量50层楼,和原始问题并没有本质区别啊,只是规模更小了。
因为还有2个蛋,所以可以在75层再测试一次,就算碎了,也还有1个蛋,再从低层往上逐层测试。
这个问题包含了规模更小的子问题,引导我们可以先从小规模的问题来思考。
1.如果只有1个蛋,要怎么测量呢?
为了一定能测试出结果,只能从1层开始逐层往上,最坏总共要100次。
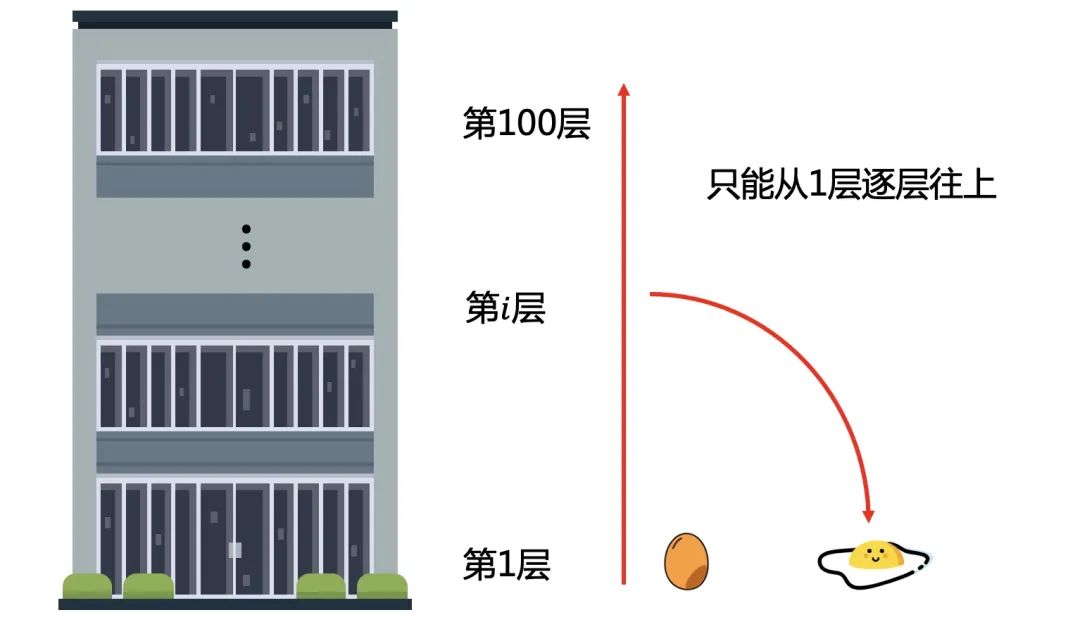
如果有n层楼,就需要n次,没有更好的方法。
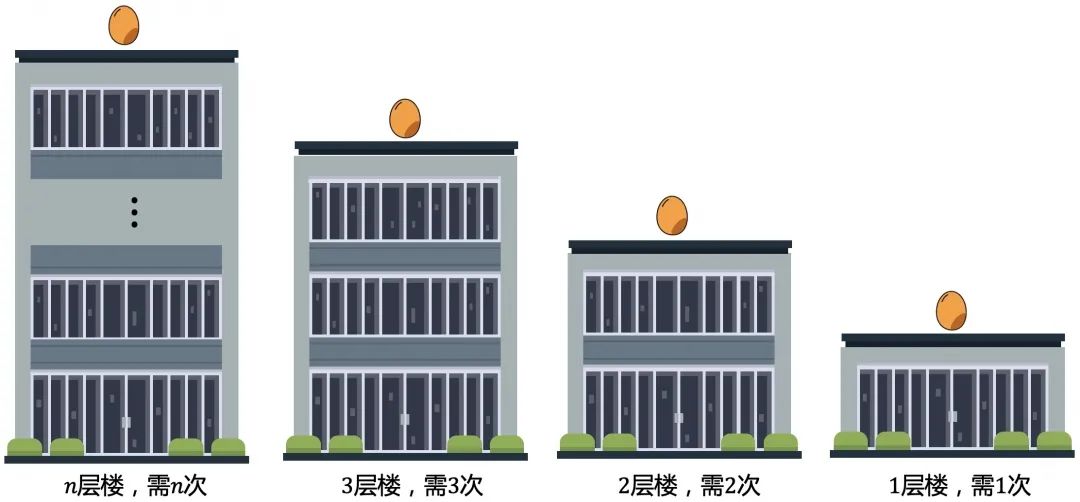
2.如果有2个蛋,考虑最小的情况,1,2,3层楼
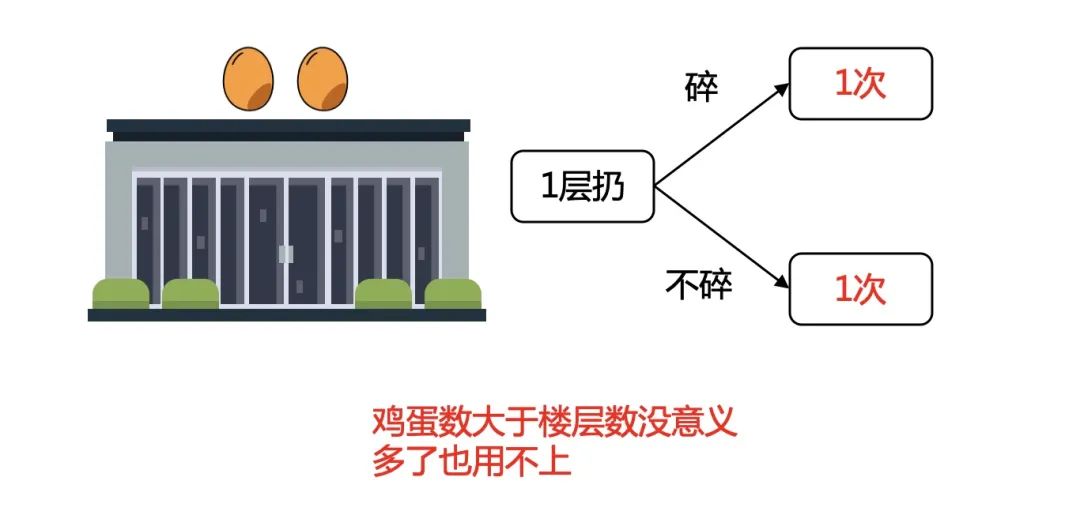
1层楼,只需1次,而且能看出鸡蛋数超过楼层数没意义。
2层楼,分别先从1、2层扔,枚举所有的情况。最好的方案是总共要2次。
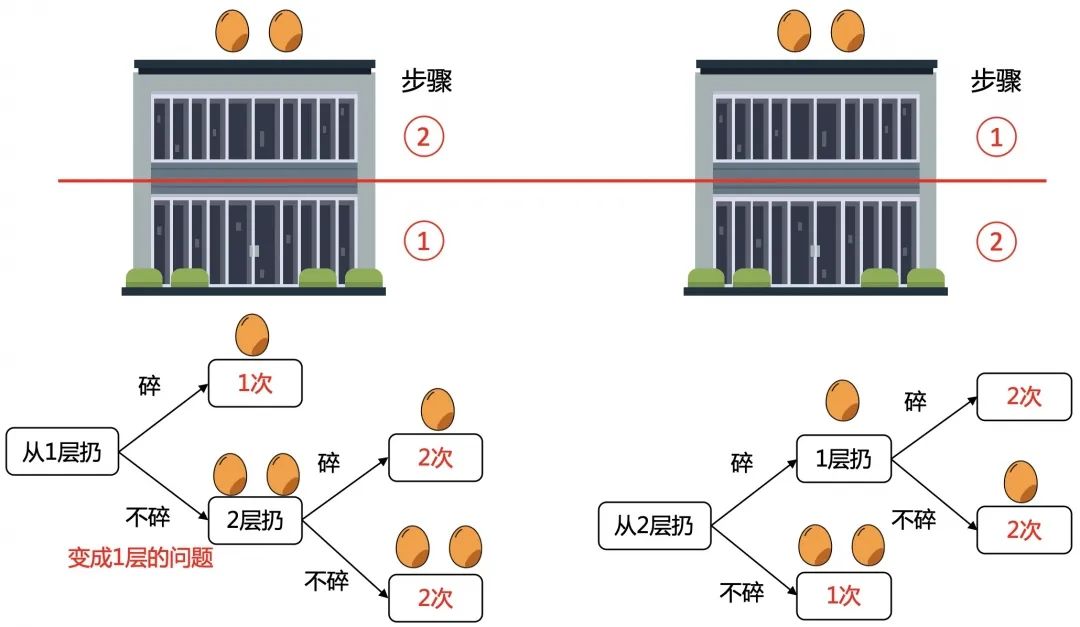
3层楼,分别先从1,2,3层扔。可以看出从1或3层扔情况是等价的。且扔下一个鸡蛋后,问题会转化成2层或1层的子问题,这个在上一步已经求出结果了。
从这3种情况中选择最好的方案,就是先从2层扔,总共要2次。
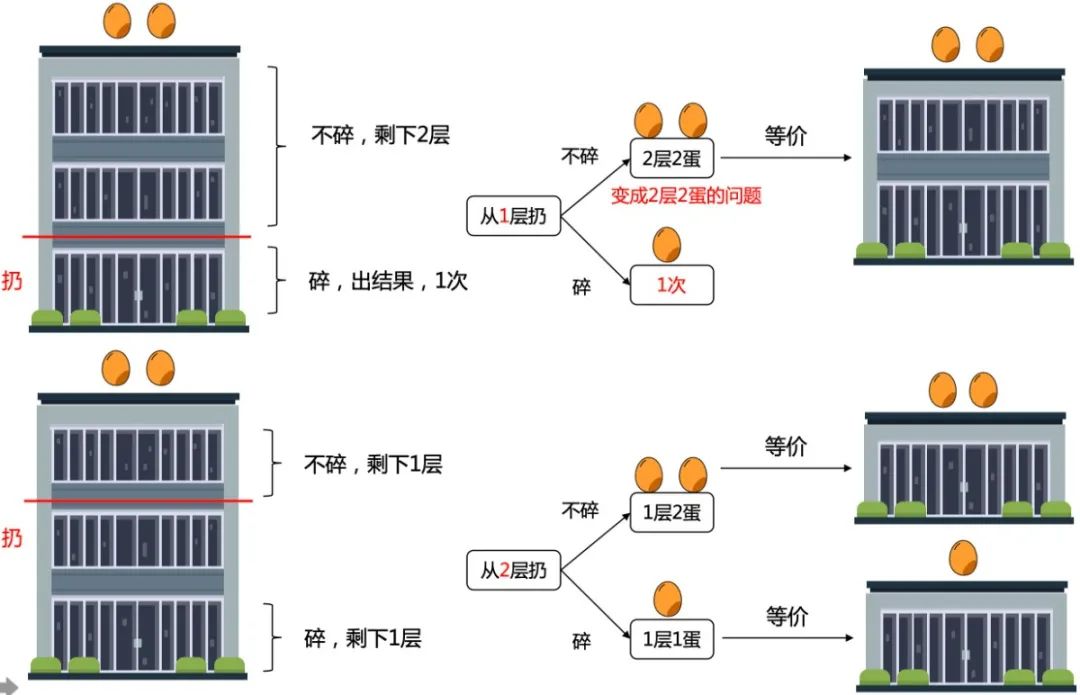
3.如此类推下去,就可以算出4,5,6...100层的最少次数。
100层如下:
从1层扔:碎,剩0层1蛋;不碎,剩99层2蛋
从2层扔:碎,剩1层1蛋;不碎,剩98层2蛋
......
从99层扔:碎,剩98层1蛋;不碎,剩1层2蛋
从100层扔:碎,剩99层1蛋;不碎,剩0层2蛋
每一层扔下去的次数为:碎和不碎中选最大的(要考虑最坏的情况),再加这一层扔的次数,需要+1。
再从上面所有情况中,选择次数最少的方案。
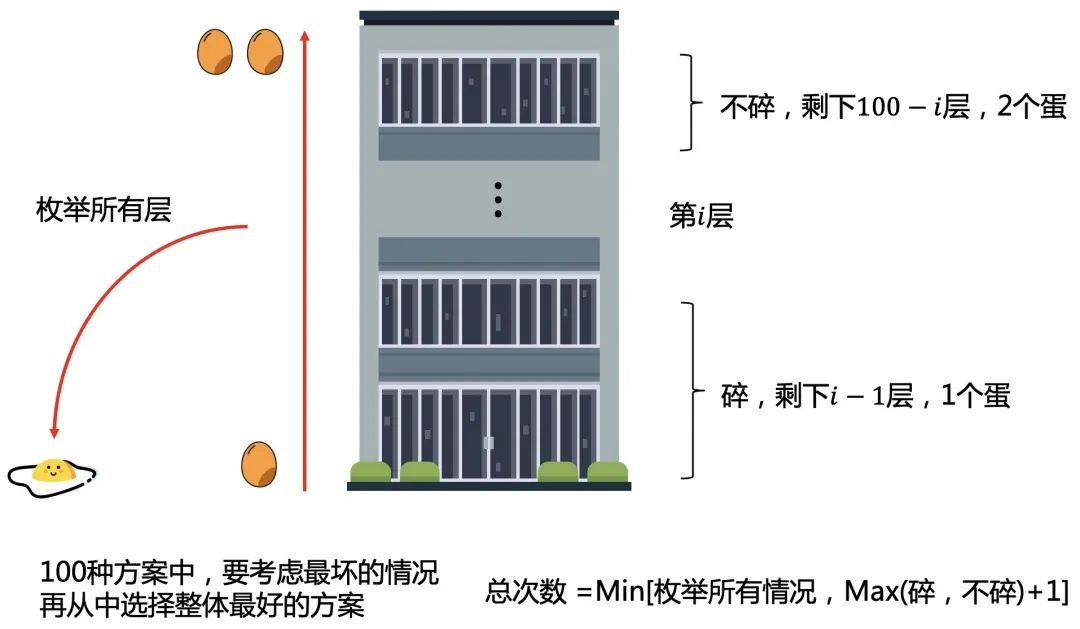
100层的具体测试方案如下:

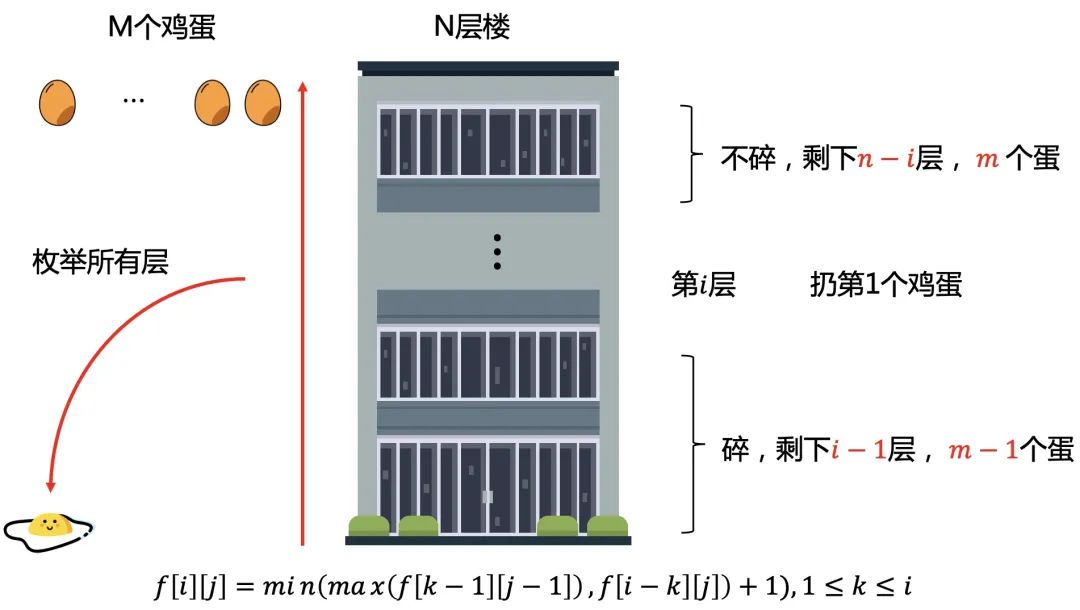
为描述方便,设表示层楼,个鸡蛋最小要测试的次数。
从第层扔下
碎, 不碎,
则

const int FLOOR = 101;
const int EGG = 3;
int f[FLOOR][EGG];
for (int i = 0; i < FLOOR; ++i) {
for (int j = 0; j < EGG; ++j) {
f[i][j] = 0x7fffffff;
}
}
// i层楼,1个鸡蛋
for (int i = 1; i < FLOOR; ++i) f[i][1] = i;
//0,1层楼,i个鸡蛋
for (int i = 1; i < EGG; ++i) {
f[0][i] = 0;
f[1][i] = 1;
}
int main() {
for (int j = 2; j < EGG; ++j) {
for (int i = 2; i < FLOOR; ++i) {
// 尝试从1到i层楼扔下,在最坏的情况中选择最好的
for (int k = 1; k <= i; ++k) {
int temp = max(f[k - 1][j - 1], f[i - k][j]) + 1;
f[i][j] = min(temp, f[i][j]);
}
}
}
cout << f[100][2] << endl;
return 0;
}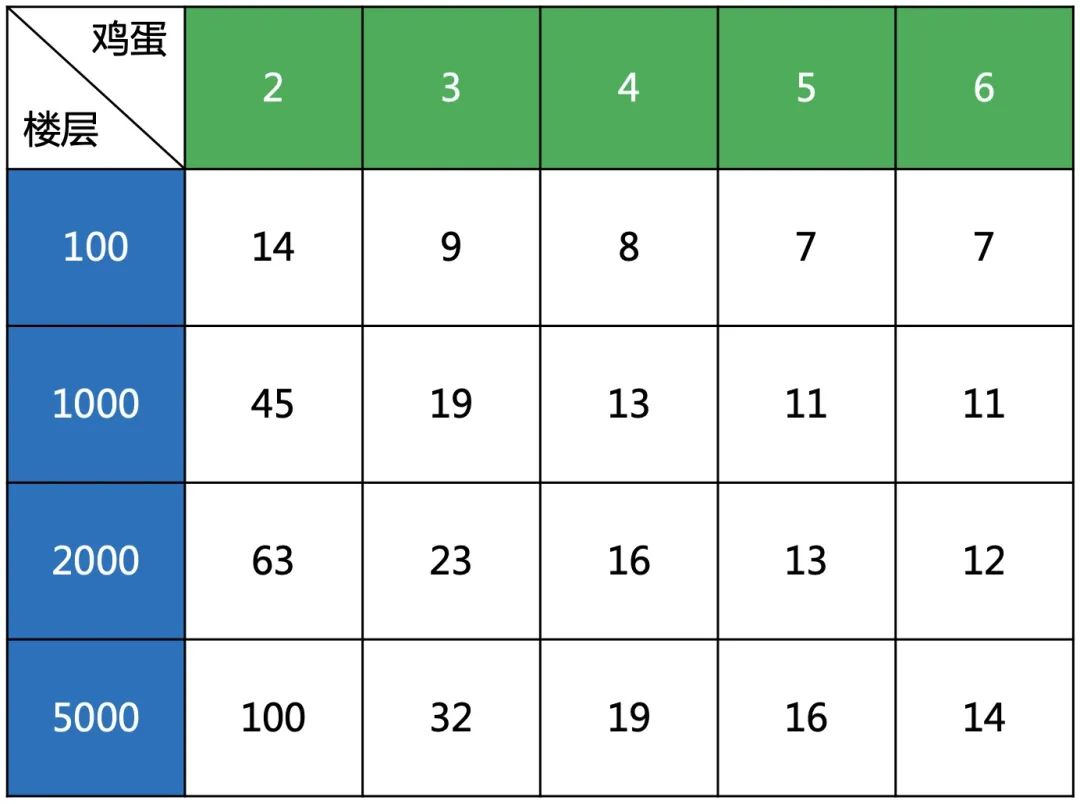
观察上面数据,会发现增加到6个蛋时,100、1000层楼的次数并没有减少,这说明最小次数是有极限的。
那怎么计算这个最小的极限呢?
想象一下,如果有无数个蛋,会是怎样呢?这时你可以不用考虑蛋碎了会不够用的问题,那你会怎么去测试?
没错,这不就是最简单的二分查找吗,每次从中间的楼层测试,那最少就是次。



