深度神经网络是否过拟合？

重磅干货，第一时间送达

作者：Lilian Weng

编译：ronghuaiyang

如果你和我一样，不明白为什么深度神经网络可以推广到样本外的数据点，而不会过拟合，请继续阅读。

如果你像我一样，有传统机器学习的经验进入深度学习领域，你可能会经常思考这样一个问题：由于一个典型的深度神经网络有这么多的参数，训练误差很容易达到完美，那么它一定会遭受大量的过拟合。如何将其推广到样本外数据点？

在理解为什么深层神经网络可以泛化的过程中，我想起了一篇关于系统生物学的有趣的论文——《生物学家能修理收音机吗?》。如果一位生物学家打算用她在生物系统上工作的方法来修理一台无线电设备的话，可能会很困难。由于无线电系统的全部机制还没有被揭示出来，小的局部功能可能会给出一些提示，但它很难显示系统内的所有交互，更不用说整个工作流程了。无论你是否认为它与DL相关，它都是一本非常有趣的读物。

我想在这篇文章中讨论一些关于深度学习模型的泛化性和复杂性度量的论文。希望它能帮助你理解为什么DNN可以泛化。

假设我们有一个分类问题和一个数据集，我们可以开发许多模型来解决它，从拟合一个简单的线性回归到在磁盘空间中存储整个数据集。哪一个更好？如果我们只关心训练数据的准确性(尤其是考虑到测试数据很可能是未知的)，那么记忆法似乎是最好的——嗯，听起来不太对。

有许多经典定理可以指导我们在这种情况下决定一个好的模型应该具有哪些类型的属性。

奥卡姆剃刀是14世纪奥卡姆的威廉提出的一种非正式的解决问题的原则：

简单的解决方案比复杂的解决方案更有可能是正确的。

当我们面对多个潜在候选理论来解释这个世界，并且必须从中选出一个时，这种说法是非常有力的。对于一个问题来说，太多不必要的假设似乎是合理的，但很难推广到其他复杂的问题中，或最终得到宇宙的基本原理。

想想看，人们花了几百年的时间才发现，天空在白天是蓝色的，而在日落时是红色的，原因是一样的(瑞利散射)，尽管两种现象看起来非常不同。人们肯定对它们分别提出了许多其他的解释，但统一而简单的版本最终胜出。

最小描述长度原则

奥卡姆剃刀原理同样适用于机器学习模型。这种概念的一个形式化版本称为最小描述长度(MDL)原则，用于比较观察到的数据中相互竞争的模型/解释。

“理解就是压缩。”

MDL的基本思想是将学习视为数据压缩。通过对数据的压缩，我们需要发现数据中具有高潜力的规律性或模式，从而推广到不可见的样本。Information bottleneck理论认为，深度神经网络首先经过训练，通过最小化泛化误差来表示数据，然后通过消除噪声来学习压缩这种表示。

同时，MDL将模型描述视为压缩交付的一部分，因此模型不能任意大。

MDL原理的两部分版本规定：设H(1)，H(2)，……H(1)，H(2)，……为能够解释数据集DD的模型列表。其中最好的假设应该是使总和最小化的假设：

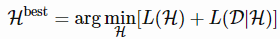
• L(H)为H模型的描述的长度，单位为bits。

• L(D|H)是用H编码时，以bits为单位来描述数据D的长度。

简单地说，“最佳”模型是包含编码数据和模型本身的“最小”模型。按照这个标准，我在本节开始时提出的记忆方法听起来很糟糕，不管它对训练数据的准确性有多高。

人们可能会说奥卡姆剃刀是错的，因为现实世界可能是任意复杂的，为什么我们必须找到简单的模型？MDL的一个有趣的观点是将模型视为“语言”，而不是基本的生成定理。我们希望找到好的压缩策略来描述一小组样本中的规律性，它们不一定是解释这种现象的“真正”生成模型。模型可能是错误的，但仍然有用(想想贝叶斯先验)。

Kolmogorov复杂度依赖于现代计算机的概念来定义对象的算法复杂度(描述性)：描述对象的最短二进制计算机程序的长度。继MDL之后，计算机本质上是最通用的数据解压器。

Kolmogorov复杂度的正式定义是：给定一个通用计算机U和一个程序p，让我们将U(p)表示为处理程序的计算机的输出，L(p)表示为程序的描述性长度。那么一个字符串ss相对于通用计算机U的Kolmogorov复杂度KU为：

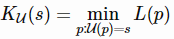
请注意，通用计算机可以模仿任何其他计算机的操作。所有现代计算机都是通用的，因为它们都可以简化为图灵机。无论我们使用哪台计算机，这个定义都是通用的，因为另一台通用计算机总是可以被编程来克隆U的行为，而对这个克隆程序进行编码只是一个常量。

Kolmogorov复杂性和Shannon信息论之间有许多联系，两者都与通用编码有关。一个惊人的事实是，一个随机变量的期望Kolmogorov复杂度大约等于它的Shannon熵。更多关于这个主题的内容不在本文讨论范围内，但是网上有很多有趣的阅读材料。

奥卡姆剃刀的另一种数学形式是Solomonoff的通用归纳推理理论(Solomonoff， 1964)。其原则是根据其Kolmogorov复杂度，选择与生成训练数据的“最短程序”相对应的模型。

深度学习模型的表达能力

与传统的统计模型相比，深度神经网络具有非常多的参数。如果我们用MDL来度量一个深度神经网络的复杂度，并将参数的个数作为模型描述的长度，这看起来会很糟糕。模型描述L(H)L(H)很容易增长失控。

然而，一个神经网络要获得高表达能力，必须有许多参数。由于深度神经网络具有捕捉任何灵活数据表示的能力，因此在许多应用中都取得了巨大的成功。

普遍逼近定理指出一个前向网络需要有：1)一个线性输出层，2)至少有一个隐含层包含有限数量的神经元，3)某个激活函数可以在n维实数空间的一个紧子集上近似任意连续函数，达到任意精度。这个定理首先被证明为sigmoid激活函数。后来的研究表明，普遍逼近性质并不是针对特定的激活函数，而是针对多层前馈体系结构。

尽管单层前馈网络足以表示任何函数，但其宽度必须呈指数级增长。普遍逼近定理不能保证模型能被正确地学习或推广。通常，添加更多的层有助于减少浅层网络中所需的隐藏神经元的数量。

为了利用普遍逼近定理，我们总是可以找到一个神经网络来表示目标函数，在任何期望的阈值下都有误差，但是我们需要付出代价—网络可能会变得非常大。

证明：两层神经网络的有限样本表达量

我们目前讨论的普遍逼近定理不考虑有限样本集，Zhang, et al. (2017)对两层神经网络的有限样本表达性给出了一个简洁的证明。

神经网络C可以表示任何函数，给定样本大小n维度为d，如果：对于每一个有限样本集合S⊆Rd，|S| = n 每个函数定义在这个样本集：f:↦R，我们可以找到一组C的权重, C (x) = f (x)， ∀x∈S。

这篇文章提出了一个定理：

存在一个具有ReLU激活和2n+d个权值的两层神经网络，它可以表示任意d维尺寸的样本上的函数。

证明：首先我们想构建一个两层神经网络C: Rd↦R。输入是一个d维向量，x∈Rd。隐含层有h个隐藏单元，权值矩阵W∈Rd×h，、偏置向量b∈Rh，使用ReLU激活函数。第二层输出一个标量值，权向量v∈Rh，且偏置为零。

一个输入向量x的在网络C的输出可以表示为：

其中W(:，i)，为d×h矩阵的第i列。

给定样本组S = {x1,…, xn}和目标值y = {y1,…, yn}，我们想找到合适的权值W∈Rd×h、b、v∈Rh，使得C (xi) =yi，∀i= 1,…,n。

让我们将所有样本点组合成一个批次，作为一个输入矩阵X∈Rn×d。设h=n，则XW - b为大小为n×n的方阵。

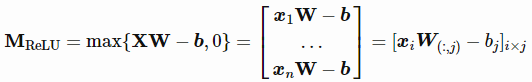
我们可以将W简化为所有列向量相同：

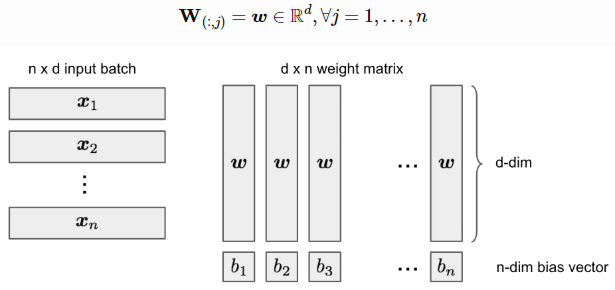
让ai=xiw，我们希望找到一个合适的w和b，使b1<a1<b2<a2⋯⋯<bn<an。这总是可以实现的，因为我们试图解决n+d个未知变量与n个约束，并且xi是独立的(即随机选择一个w，排序xiw，然后在两者之间设置bj值)。然后MReLU变成一个下三角矩阵：

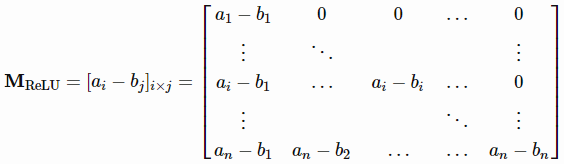
当det(MReLU)≠0时，为非奇异方阵，所以我们总能找到合适的v来求解vMReLU=y(即MReLU的列空间全部为Rn，可以找到列向量的线性组合，得到任意y)。

正如我们所知，两层神经网络是通用的逼近器，因此，它们能够完美地学习非结构化随机噪声也就不足为奇了。如果对图像分类数据集的标签进行随机变换，深度神经网络的高表达能力仍然可以使其训练损失接近于零。这些结果不随正则化项的添加而改变。

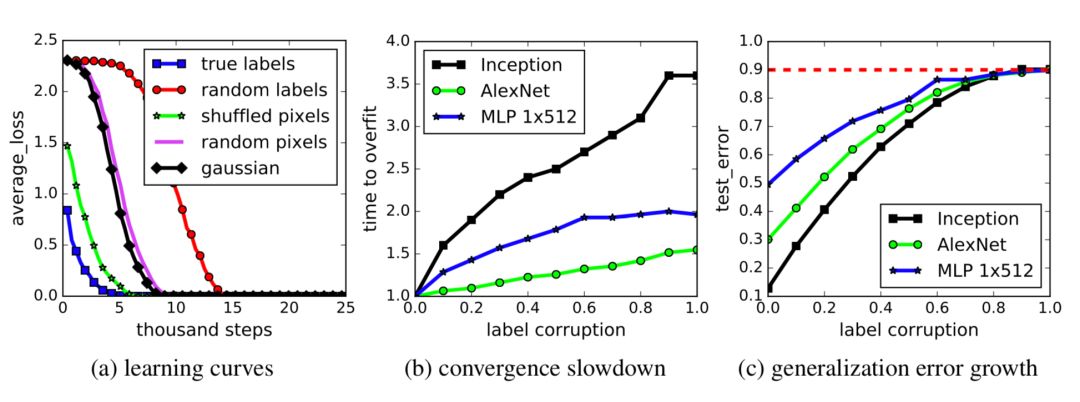
深度学习模型是高度参数化的，常常可以在训练数据上得到完美的结果。在传统的观点中，就像偏差-方差权衡一样，这可能是一场灾难，没有任何东西可以概括为不可见的测试数据。然而，通常情况下，这种“过拟合”(训练误差= 0)的深度学习模型在样本外测试数据上仍然表现良好。嗯……有意思，为什么?

深度学习的现代风险曲线

传统的机器学习使用下面的u型风险曲线来衡量偏差-方差权衡，并量化模型的可泛化程度。如果有人问我如何判断一个模型是否过拟合，我首先想到的就是这个。

随着模型的变大(增加的参数越多)，训练误差减小到接近于零，但是当模型的复杂度超过“欠拟合”和“过拟合”的阈值时，测试误差(泛化误差)开始增大。在某种程度上，这是与奥卡姆剃刀很好的对齐。

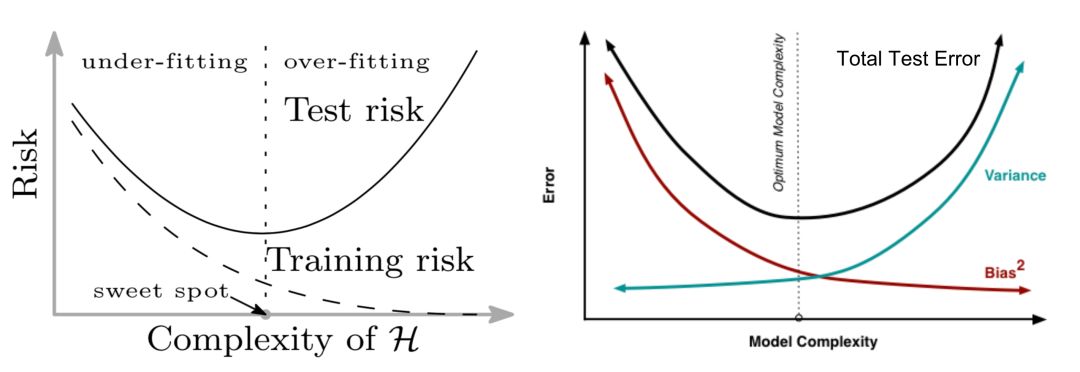
不幸的是，这不适用于深度学习模型。Belkin et al. (2018)调和了传统的偏方差权衡，提出了一种新的用于深度神经网络的双u型风险曲线。一旦网络参数数量足够多，风险曲线进入另一种状态。

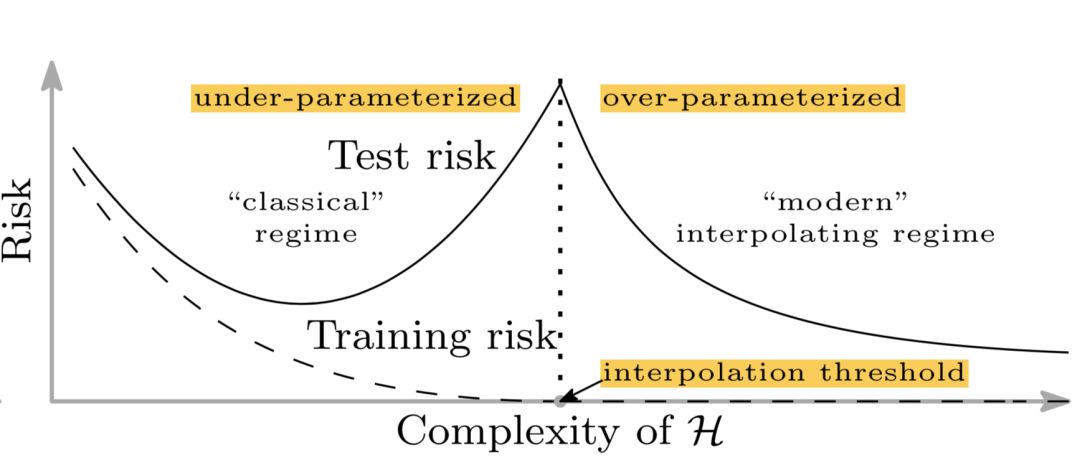
该论文称，这可能有两个原因：

• 参数的数量并不能很好地衡量归纳偏差，归纳偏差定义为用于预测未知样本的学习算法的一组假设。

• 使用一个更大的模型，我们可能能够发现更大的函数类，并进一步找到插值函数具有更小的范数，从而“更简单”。

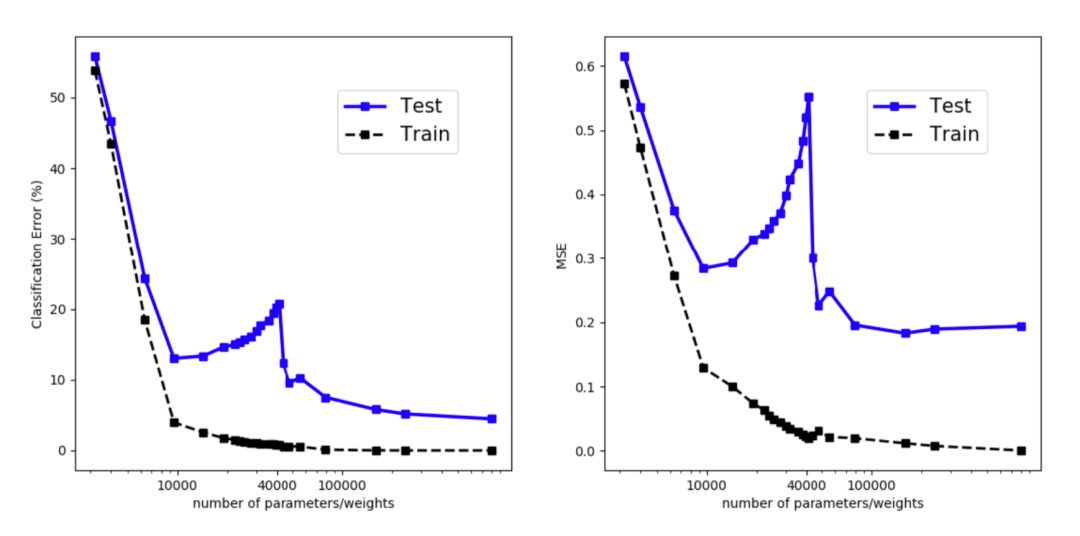
实验观察到双u型风险曲线，如图所示。然而，我花了很大的力气来重现这个结果。生活中存在一些迹象，但为了生成一条与定理类似的相当平滑的曲线，必须注意实验中的许多细节。

正则化不是泛化的关键

正则化是控制过拟合和提高模型泛化性能的常用方法。有趣的是，一些研究(Zhang, et al. 2017)表明，显式正则化(即数据增强、权重衰减和dropout)对于减少泛化误差既不是必要的，也不是充分的。

以CIFAR10上训练的Inception模型为例(参见图5)，正则化技术有助于样本外的泛化，但作用不大。没有一个单独的正则化看起来是独立于其他项的。因此，正则化器不太可能是泛化的“基本原因”。

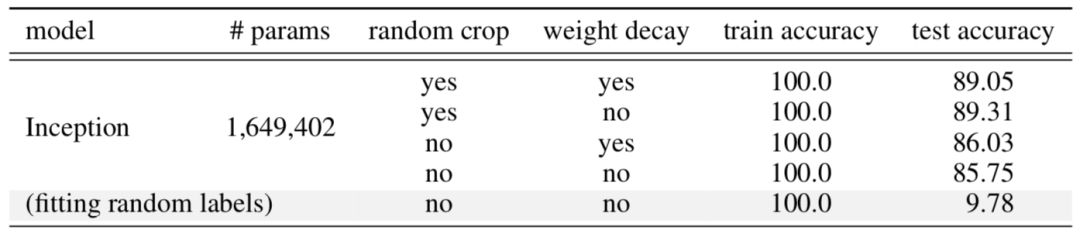
在深度学习领域中，参数个数与模型过拟合无关，说明参数个数不能反映深度神经网络的真实复杂度。

除了参数个数，研究人员还提出了许多方法来量化这些模型的复杂性，如模型的自由度(Gao & Jojic, 2016），或prequential码(Blier & Ollivier, 2018)。

我想讨论一下最近关于这个问题的一个方法，名为intrinsic dimension (Li et al, 2018)。内在维度直观，易于测量，同时还揭示了不同尺寸模型的许多有趣特性。

考虑具有大量参数的神经网络，形成一个高维参数空间，学习发生在这个高维的“目标视图”上。参数空间流形的形状至关重要。例如，更平滑的流形有利于优化，因为它提供了更多的预测梯度，并允许更大的学习速率——这被认为是batch normalization成功地稳定训练的原因。

尽管参数空间很大，但幸运的是，我们不必过多担心优化过程陷入局部最优，正如已经显示的那样，目标视图中的局部最优点几乎总是位于鞍点而不是谷点。换句话说，总是有一个维度子集包含离开局部最优并继续探索的路径。

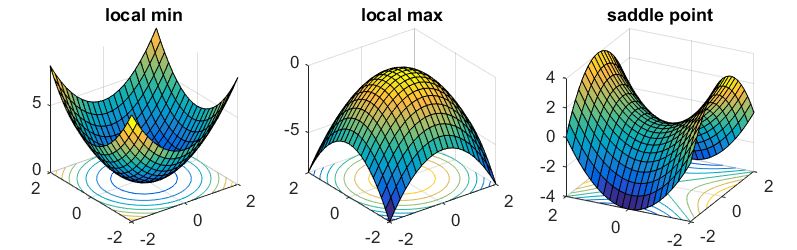
度量内在维度的一个直觉是，由于参数空间具有如此高的维数，可能没有必要利用所有维数来有效地学习。如果我们只在一片目标视图中游走，仍然可以学习到一个好的解决方案，那么得到的模型的复杂性很可能比通过参数个数得到的模型要低。本质上这就是内在维度试图评估的东西。

比如说模型有D个维度，及其参数表示为θ(D)。对于学习来说，一个小的d维子空间是随机采样得到的，其中d < D。在优化更新的过程中，只用到了较小的子空间θ(d)来更新模型参数，而不是根据所有D个维度来进行梯度的更新。

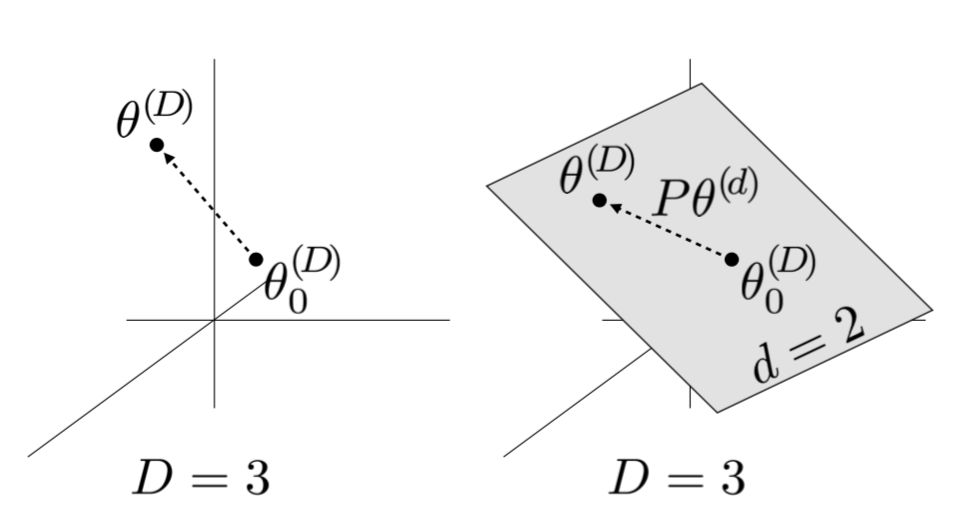
梯度更新公式如下：

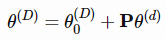
其中θ0(D)是初始化值，P是D×d的投影矩阵，在训练前进行随机采样。θ0(D)和P是不可训练的，在训练中是固定的。θ(d)初始化为全零。

通过搜索d=1,2，…，D的值，将解出现时对应的d定义为内在维度。

事实证明，许多问题的内在维度比参数的数量要小得多。例如，在CIFAR10图像分类中，650k+参数的全连接网络只有9k的固有维数，而包含62k参数的卷积网络的固有维数更低，只有2.9k。

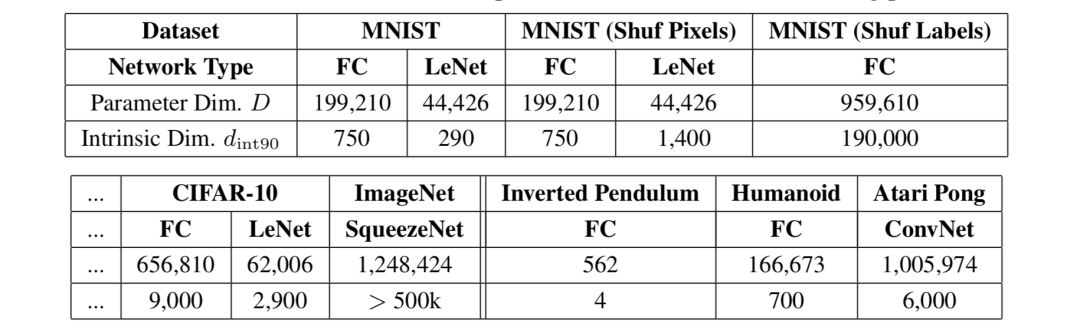
对内在维度的度量表明，深度学习模型比表面上看起来要简单得多。

Zhang等(2019)研究了参数在不同层中的作用。论文提出的基本问题是:“所有层都是平等的吗？”简短的回答是：不是。模型对某些层的变化更敏感，而对其他层的变化则不敏感。

本文提出了两种类型的操作，可应用于第ℓ层的参数上，ℓ= 1,…,L，在t时刻，θt(ℓ)用来测试他们对模型的鲁棒性的影响：

重初始化 :重置参数初始值，θt(ℓ)←θ0(ℓ)。这层重新初始化后的网络性能被称为重初始化ℓ层的鲁棒性。

重随机化 :对层参数进行随机采样θt(ℓ)←θ~(ℓ)∼P(ℓ)。相应的网络层的性能称为重随机化的鲁棒性。

层可以通过这两个操作分为两类：

• 鲁棒层:重新初始化或随机化层后，网络没有或只有微不足道的性能下降。

• 关键层:其他情况。

在全连接和卷积网络上也观察到类似的模式。重新随机化任何层完全破坏模型性能，因为预测立即下降到随机猜测。更有趣和令人惊讶的是，当应用重新初始化时，只有前几层(最接近输入层)是关键的，而重新初始化更高的层只会导致性能微不足道的下降

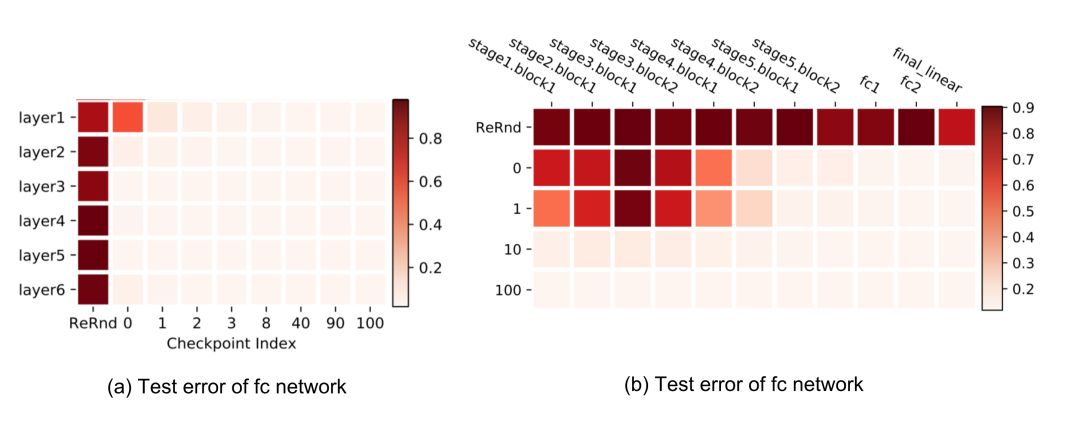
ResNet能够使用非相邻层之间的快捷方式跨网络重新分布敏感层，而不只是在底层。在残差块结构的帮助下，网络对再随机化具有均匀鲁棒性。只有每个残差块的第一层仍然对重新初始化和重新随机化敏感。如果我们把每个残差块看作一个局部子网络，那么健壮性模式就像上面的fc和conv网络。

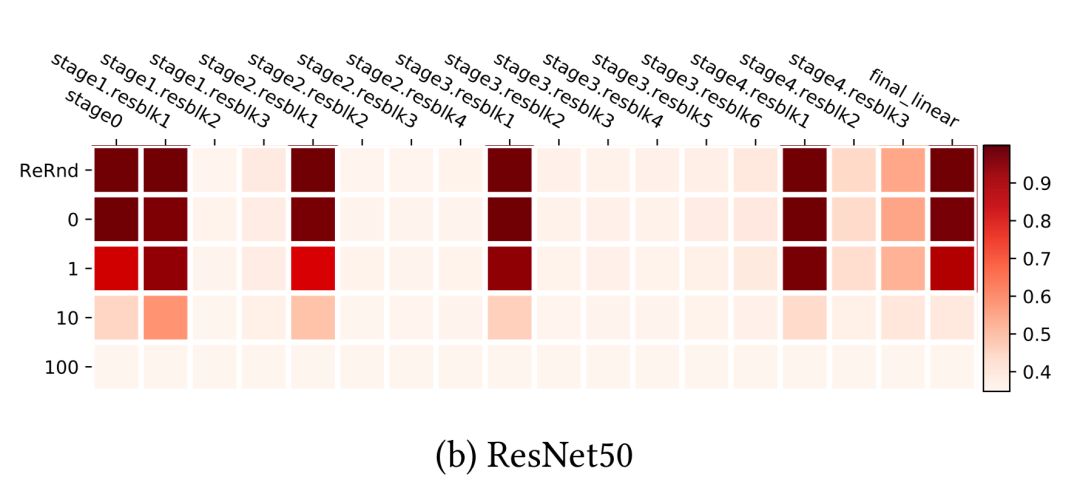
基于深度神经网络中很多顶层对模型重新初始化后的性能并不重要的事实，本文粗略地得出结论：

Based on the fact that many top layers in deep neural networks are not critical to the model performance after re-initialization, the paper loosely concluded that:

“采用随机梯度训练的超容量深度网络由于其临界层数的自限制，具有较低的复杂度。”

我们可以考虑将重初始化作为减少有效参数数量的一种方法，从而使观察结果与所演示的内在维度保持一致。

在看到上面所有有趣的发现之后，复现它们应该会很有趣。有些结果比其他结果更容易复现。细节如下所述。我的代码可以在github上找到：https://github.com/lilianweng/generaliz-experiment。

深度模型的新风险曲线

这是最难复现的。作者确实给了我很多很好的建议，我很感激。以下是他们实验中一些值得注意的设置：

• 没有正则化项，如权值衰减，dropout。

• 在图3中，训练集包含4k样本。它只采样一次，并对所有模型进行固定。评估使用完整的MNIST测试集。

• 每个网络都经过长时间的训练，实现训练风险接近零。对于不同大小的模型，学习率的调整是不同的。

• 为了使模型对欠参数化区域的初始化不那么敏感，他们的实验采用“权值重用”方案：将训练较小神经网络得到的参数作为训练较大神经网络的初始化。

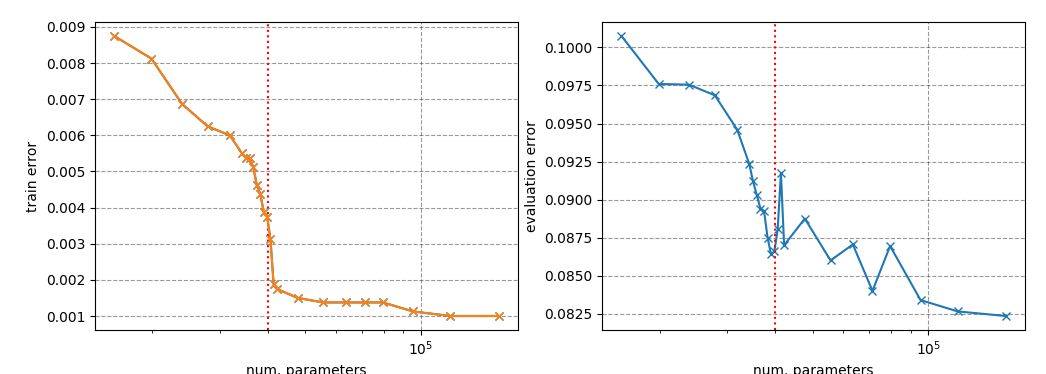
我没有对每个模型进行足够长的训练或调整，以获得完美的训练性能，但评估误差确实显示了插值阈值周围的特殊扭曲，与训练误差不同。例如，对于MNIST，阈值是训练样本的数量乘以类的数量(10)，即40000。

x轴是模型参数的个数取对数。

层不是生来平等的

这个很容易复制。参见我的实现此处：https://github.com/lilianweng/generalizing-ent/blob/master/layer_equality.py。

在第一个实验中，我使用了一个三层的fc网络，每层256个单元。第0层是输入层，第3层是输出层。该网络在MNIST上训练了100个epochs。

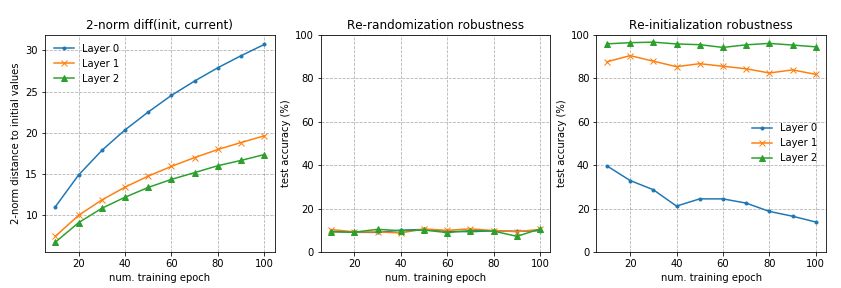
在第二个实验中，我使用了一个四层的fc网络，每层128个单元。其他设置与实验1相同。

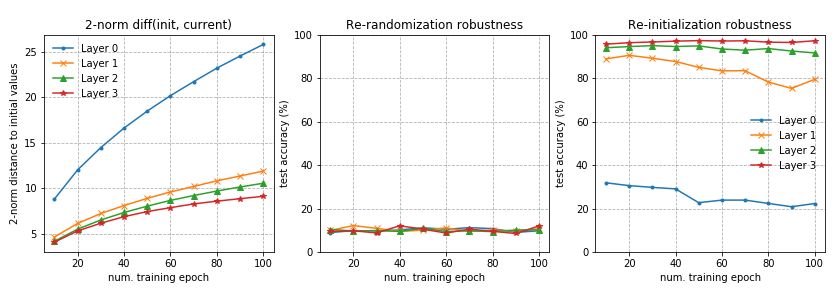
内在维度测量

为了正确地将d维子空间映射到全参数空间，投影矩阵p应该具有正交列。因为Pθ(d)是P的列的总和对应的标量值的向量，最好充分利用P的正交的子空间列。

我的实现采用了一种简单的方法，从标准正态分布中抽取一个具有独立项的大矩阵作为样本。这些列在高维空间中是独立的，因此是正交的。当维度不是太大时，这种方法有效。在使用大型的d进行探索时，有创建稀疏投影矩阵的方法，这正是本文所建议的。

实验运行在两个网络上：(左)一个两层的fc网络，每层64个单元，(右)一个单层的fc网络，128个隐藏单元，训练在MNIST的10%。对于每个d，模型都要经过100个epochs的训练。参见代码。

—END—

英文原文：https://lilianweng.github.io/lil-log/2019/03/14/are-deep-neural-networks-dramatically-overfitted.html