嘿,来聚个类!
所谓人以类聚,物以群分。人们都喜欢跟自己性格相合,爱好相同的人在一起。
俗称:处得来!靓仔, 我很中意你啊~

A 某和 B 某青梅竹马,A 某通过 B 某认识了 C 某,发现兴趣爱好出奇一致,这三人就搞到了一起,成为了一个形影不离的小团体。这个小团体的形成,是自下而上的迭代过程。
200 个人当中,可能有 10 个小团体,这些小团体的形成可能要好几个月。
这种「找朋友」的过程,就是今天我们要讲的主题:聚类算法。
聚类
聚类算法:就是把距离作为特征,通过自下而上的迭代方式(距离对比),快速地把一群样本分成几个类别的过程。
更严谨,专业一些的说法是:
将相似的对象归到同一个簇中,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同数据尽量分离。

很显然,聚类是一种无监督学习。
为了防止新手看不懂,这里简单解释一下:
对于有标签的数据,我们进行有监督学习,常见的分类任务就是监督学习; 而对于无标签的数据,我们希望发现无标签的数据中的潜在信息,这就是无监督学习。
聚类是一种非常常用,且好用的算法。
举个例子:
给你 1 万张抠脚大汉的图片和 1 万张可爱萌妹的图片,这 2 万张图片是混在一起的。

好了,我现在想把所有可爱萌妹的图片全部扔掉,因为我只爱抠脚大汉!
这种时候,就可以用到聚类算法。
这是一个比较好理解的例子,专业一点的需求场景,比如人脸识别。
人脸识别需要大量的人脸数据,在数据准备阶段,就可以利用聚类算法,辅助标注 + 清洗数据。

这是一种常规的数据挖掘手段。
我对一些常见的聚类算法,进行了整理:
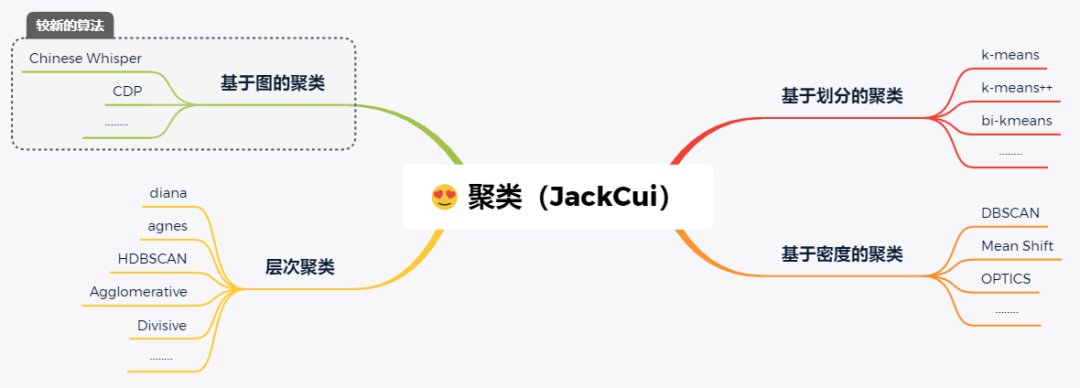
前面讲到,聚类算法是根据样本之间的相似度,将数据进行归类的。
而相似度的度量方法,可以大致分为:
距离相似性度量 密度相似性度量 连通相似性度量
不同类型的聚类算法,采用的样本间的相似度度量方法是不同的。
聚类算法很多,一篇文章无法讲述详尽,今天带大家从最基础的 Kmeans 学起。
K-Means
K-Means 是一个非常经典的聚类算法,别看它古老,但很实用。
这么说吧,我现在做项目,一些小功能,偶尔还会用到 K-Means。
K-Means 即K-均值,定义如下:
对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大
K-Means 聚类的步骤如下:
随机的选取K个中心点,代表K个类别; 计算N个样本点和K个中心点之间的欧氏距离; 将每个样本点划分到最近的(欧氏距离最小的)中心点类别中——迭代1; 计算每个类别中样本点的均值,得到K个均值,将K个均值作为新的中心点——迭代2; 重复步骤2、3、4; 满足收敛条件后,得到收敛后的K个中心点(中心点不再变化)。
K-Means 聚类可以用欧式距离,欧式距离很简单,二维平面就是两个点的距离公式,在多维空间里,假设两个样本为a(x1,x2,x3,x4...xn),b(y1,y2,y3,y4...yn),那么他们之间的欧式距离的计算公式是:
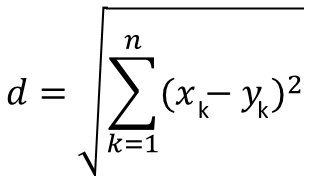
可以用下面的图很好地说明:
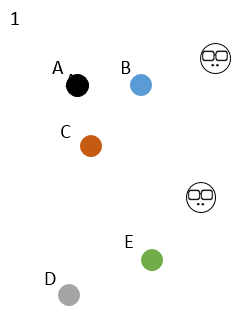
有 ABCDE 5个样本,一开始选定右边的 2 个初始中心点,K=2,大家颜色都不一样,谁都不服谁;
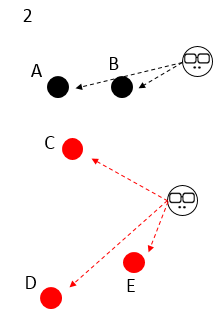
5 个样本分别对比跟 2 个初始中心点的距离,选距离近的傍依,这时 5 个样本分成红黑 2 群;
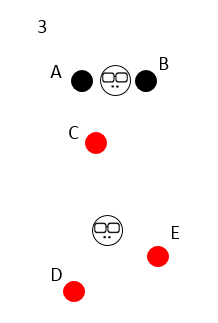
然后开始换老大啦,2 个初始中心点消失,重新在 2 个类分别中心的位置出现 2 个新的中心点,这 2 个新的中心点离类别里样本的距离之和必须是最小的;
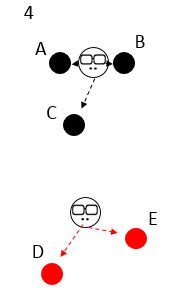
新的老大出现,类别的划分也不一样啦,C 开始叛变,傍依了新老大,因为他离新老大更近一点;
新的老大消失,新新老大出现,发现划分的类别没有变化,帮派稳定,于是收敛。
用代码简单实现一下:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()
生成一些随机点。
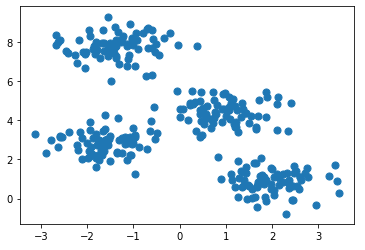
然后使用 K-Means 进行聚类。
from sklearn.cluster import KMeans
"""
KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300,
tol=0.0001, precompute_distances='auto', verbose=0,
random_state=None, copy_x=True, n_jobs=1, algorithm='auto')
Parameters:
n_clusters: 聚类个数
max_iter: 最大迭代数
n_init: 用不同的质心初始化值运行算法的次数
init: 初始化质心的方法
precompute_distances:预计算距离
tol: 关于收敛的参数
n_jobs: 计算的进程数
random_state: 随机种子
copy_x:是否修改原始数据
algorithm:“auto”, “full” or “elkan”
”full”就是我们传统的K-Means算法,
“elkan”elkan K-Means算法。默认的
”auto”则会根据数据值是否是稀疏的,来决定如何选择”full”和“elkan”,稠密的选 “elkan”,否则就是”full”
Attributes:
cluster_centers_:质心坐标
Labels_: 每个点的分类
inertia_:每个点到其簇的质心的距离之和。
"""
m_kmeans = KMeans(n_clusters=4)
from sklearn import metrics
def draw(m_kmeans,X,y_pred,n_clusters):
centers = m_kmeans.cluster_centers_
print(centers)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
#中心点(质心)用红色标出
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
print("Calinski-Harabasz score:%lf"%metrics.calinski_harabasz_score(X, y_pred) )
plt.title("K-Means (clusters = %d)"%n_clusters,fontsize=20)
plt.show()
m_kmeans.fit(X)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=4, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
y_pred = m_kmeans.predict(X)
draw(m_kmeans,X,y_pred,4)
聚类运行结果:
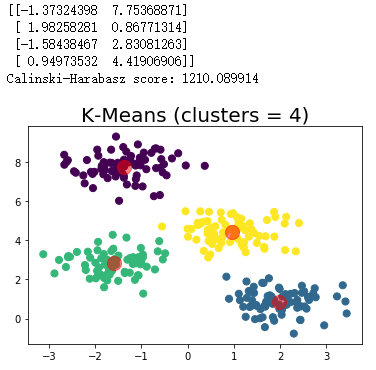
总结
K-Means 聚类是最简单、经典的聚类算法,因为聚类中心个数,即 K 是需要提前设置好的,所以能使用的场景也比较局限。
比如可以使用 K-Means 聚类算法,对一张简单的表情包图片,进行前后背景的分割,对一张文本图片,进行文字的前景提取等。
K-Means 聚类能使用的距离度量方法不仅仅是欧式距离,也可以使用曼哈顿距离、马氏距离,思想都是一样,只是使用的度量公式不同而已。
聚类算法有很多,且看我慢慢道来。
想看我讲解其它好玩实用的聚类算法,例如 CDP 等,不妨来个三连,给我来点动力。
我是 Jack,我们下期见。

推荐阅读
• 五年了• 万字长文,60分钟闪电战• 让猛男娇羞的AI算法
