55张图,一次让你心里有点B树
什么是B树？
难道你有心里没点……那可不行！
B树正式认识
首先纠正一个概念，有些人会说什么B树和B-树，这俩其实是一样的，都是B树就对了！
对于B树，它是一种自平衡的树，也就是平衡被破坏后需要进行操作重新达到平衡！学习这个B树之前，你需要了解：
- 二叉查找树
- AVL树
- 2-3树
当然，上述你不了解你也可以直接学习B树，只不过会更加费劲而已，了解了上述三种树之后再看B树，你就会觉得清晰很多！
首先B树和2-3更加相似一点，主要就是体现在不像之前咱们常见的那种二叉树，只有两个叉，也就是只有左右孩子，像2-3树就可以拥有三个孩子节点～
对于B树也是类似的，不是只有两个叉，可以有2个以上的子节点！
另外，对于B树这种数据结构，经常用在数据库和文件系统上～
主要是因为B树每个节点可以存储多个数据以及可以有2个以上的子节点从而减少磁盘IO，进而提升搜索性能等！
总结起来一句话就是：
B树是一种多路的平衡搜索树
解读下这里的几个概念，首先什么是多路，其实简单，就是可以有多个叉，不仅仅是二叉树那样最多两个子节点，多路就可以有多个节点！
然后是平衡，这个就是会有一个平衡的条件，就是达到什么样才算平衡！
比如之前学习的AVL树就是左右字数高度差不大于1，一旦不满足平衡就要想办法让其平衡，这就是所谓的平衡树!
那搜索树呢？
记住核心就是比左边的大，比右边的小！
ok，关于什么是B树，我们通过文字叙述了一遍！那接下来我们画图来给大家直观的看下，B树长什么样子：
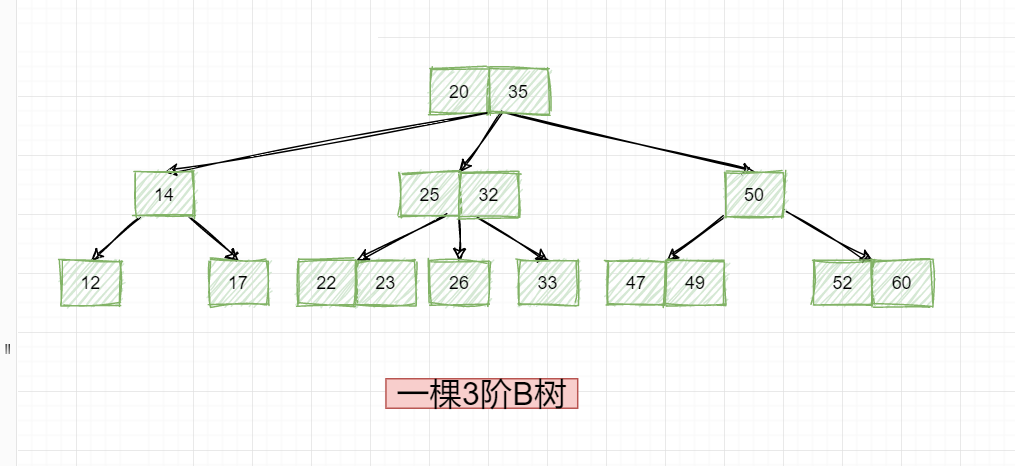
以上就是一棵3阶B树，那有人会不会说，有没有4阶B树？当然有，如下：
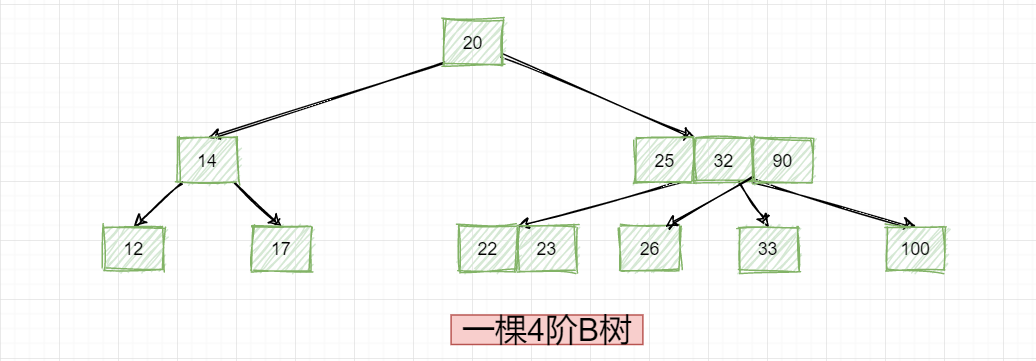
看到这个大家就可以大胆猜测一下，**这几个几阶B树是如何判断的？**可以想一下咱们之前讲解2-3树的时候提到的2-节点和3-节点！
说到这里，大家也可以思考下，这个B树和2-3树的区别～
对于2-3树，最多的就是3-节点可以拥有两个数据和三个子节点，但是我们看这个B树，是不是还可以一个节点拥有三个数据以及四个子节点，比如这个：
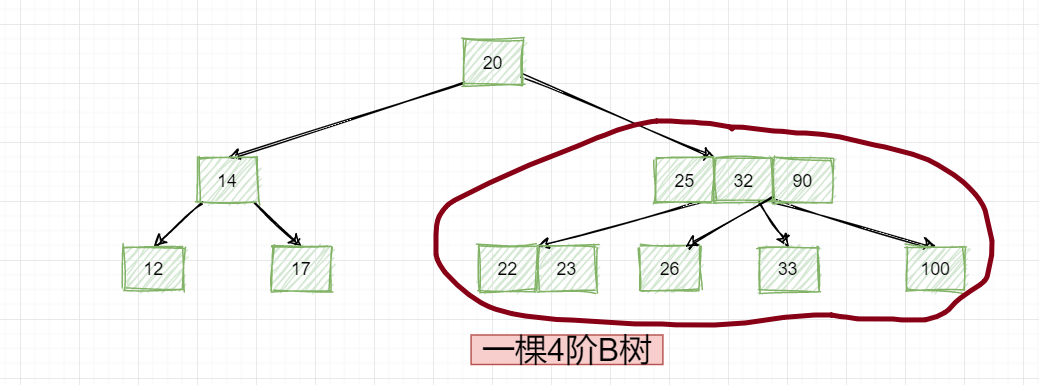
然后我们再看，这些节点保存的数据有什么特点？是不是依然是比左边的都大，比右边的都小？
有人可能疑惑，这一个节点存好多数据怎么比较，这个其实也简单，如果存多个数据，我们就拿最大和最小的数据去比较，比如这个：
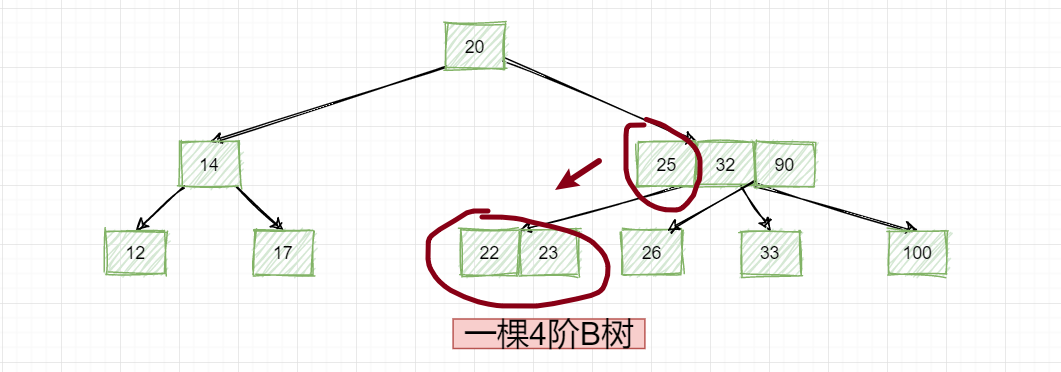
最小的数据25是不是比左字数中所有的数据都大，然后再看：
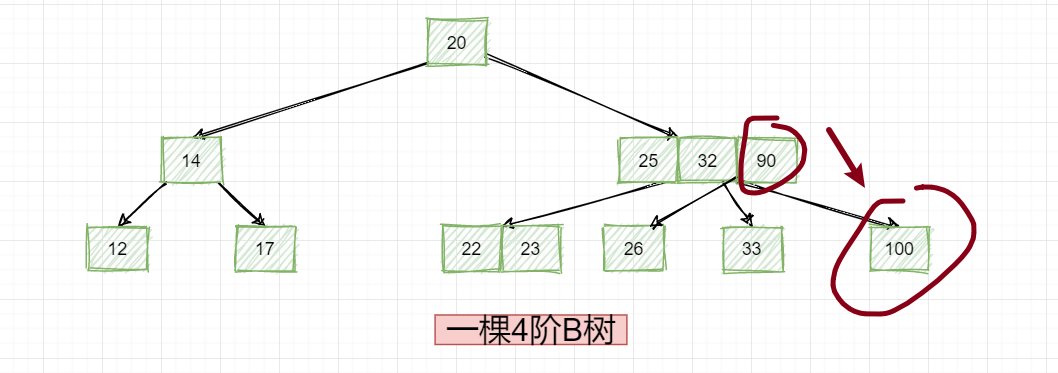
最大的数据90是不是也要比右子树中的数据都小！那接下来稍微有点难比较的就是中间节点的比较，其实也很简单，我画个图：
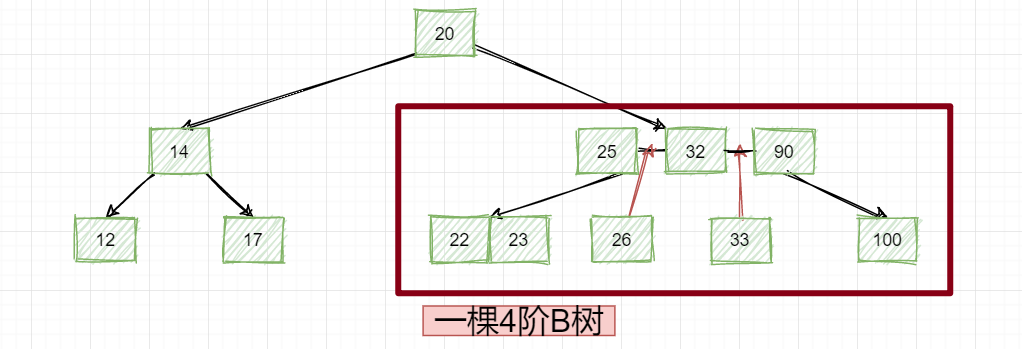
该节点的三个数值分别是25,32和90，有三个数据，然后有四个子节点，最小的数据25一定是大于左子树中的所有数值（22和23）～
最大的数据90一定是小于右子树中所有的数值（100），那中间的俩节点数值26和33正好是处于25和32之间，以及32和90之间！
如果把它给压平了一定是从左至右，依次变大的，也就是这样：
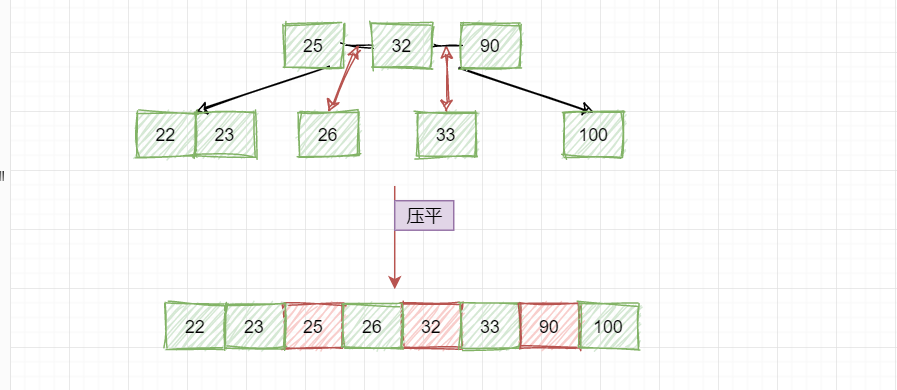
所以，B树是拥有二叉查找树的性质的，并且这个大小关系和2-3树是一样的，这就是B树了，以后别人再问你心里有没有点……知道该怎么回答了吧！
B树的直观印象
接下来我们来看下B树一眼看上去，有啥特点，首先，还是上面给大家举例的这棵3阶B树：
就它，一眼看上去，有啥特点，首先想下2-3树，是不是和2-3树一样，绝对平衡，也就是每一个节点的所有子树高度都是一致的～
另外还有一个特点，就是B树是不是比较矮，如果上面这些数据存储到二叉树的话，一定是比较高的，就是细长细长的！
为什么在B树这里就比较矮？想必你也想到了，就是因为对于B树来说，它的一个节点可以存储多个数据，以及每个节点可以有多个子节点，所以B树一般比较矮，比较宽！
对了，不知道大家看到这里会不会有这样一个疑惑：
为什么叫做B树啊，咋不是C树，D树？
有一种说是说这种树非常平衡，英文叫做Balanced Tree，这个Balanced翻译过来就是平衡的意思～
其实平衡树有很多，比如2-3树，以及红黑树和AVL树，不过这些基于个人特色都有自己的名字，所以就管这种树叫做B树了！
这个大家了解下即可！
几阶B树分析
接下来我们再看这个3阶B树：
前面也给大家提到过，有3阶B树，也有4阶B树，那这个几阶是怎么判断的呢？
我们抛开其他的不说，就单纯来看我们的这个B树，比如上面的这个3阶B树，为什么叫做3阶B树，怎么不是4阶，或者5阶？
也就是说，这个3代表的是什么？
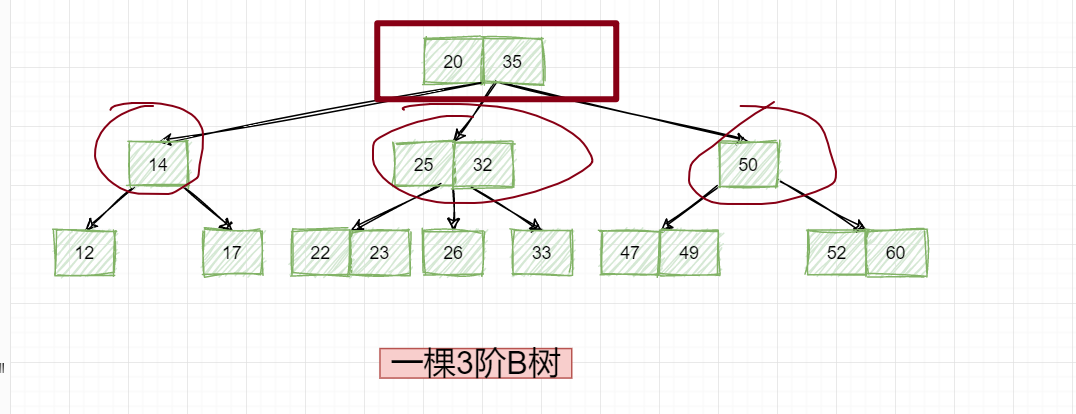
画个图说明一下就是，这棵树中，某个节点拥有的最大子节点说，我们看上面的图，是不是可以发现在这棵书中，最多的子节点只有3个，所以叫做3阶B树，再看下面的：
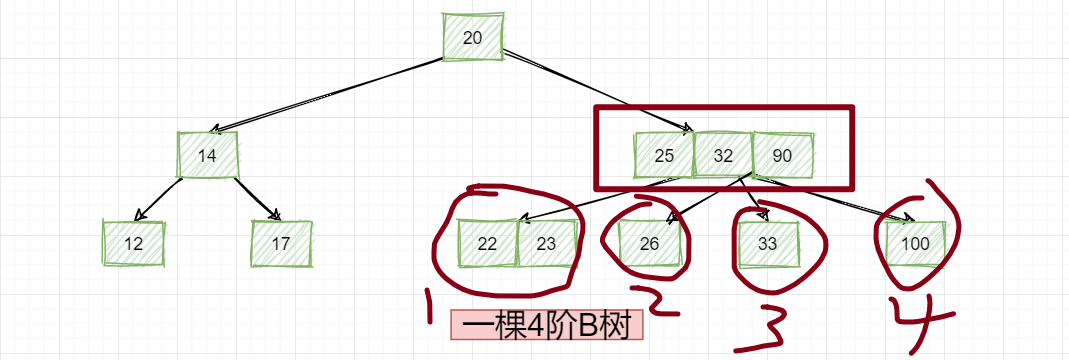
那这个为什么叫做4阶B树？就是因为在这棵树中，最多存在拥有4个子节点的节点，所以叫做4阶B树！
所以到这里大家就要清楚了，判断是几阶B树，就看这棵树中，某个节点含有的最大子节点数，比如某个节点最多含有5个子节点，那这棵B树就是5阶B树！
对了，要知道，这个几阶最少也是2阶的！
到了这里不知道大家有没有发现，我们这里所说的3阶B树其实就是2-3树！
这就是B树
ok，到了这里，我们已经大致了解了什么是B树，可能你还是感觉到有点模糊，那么现在就正儿八经的给大家明确下，什么样的树才是B树！
我们同样把这个3阶B树给放到这里：
然后看着这棵3阶B树，我们来看下，到底什么样的树才能叫做B树：
1、每个节点可以存储多个数据值，比如三个，四个等等，比如一棵3阶B树，那每个节点的数据值最多肯定不能大于2啊，但是最少也不能少于1，所以这里关于每个节点存储的数据元素个数遵循如下规则：一棵m（>=2）阶的B树，非根节点的数据元素个数为x，则(m/2)-1 <= x <= m-1（m/2 向上取整，比如3/2 结果是2）
2、根节点最少要存储一个数据值，也就是拥有两个孩子节点
3、一个非叶子结点，如果它有m个子节点的话，那么该节点就有（m-1）个元素
4、每个节点的数据值从小到大排列，与子树节点中的数据大小关系按照上文中的分析
5、所有叶子节点都位于同一层，也就是根节点到每个叶子节点的长度都相同
第一点很重要，然后这里要特别说一下第5条，也就是“所有叶子节点都位于同一层，也就是根节点到每个叶子节点的长度都相同”
什么意思呢？
其实2-3树就是一种最简单的B树，它们都有这个特性，就是绝对平衡，也就是所有叶子节点必须在同一层，比如上面我们说的3阶B树，如果是这样的，它就不是一棵B树：
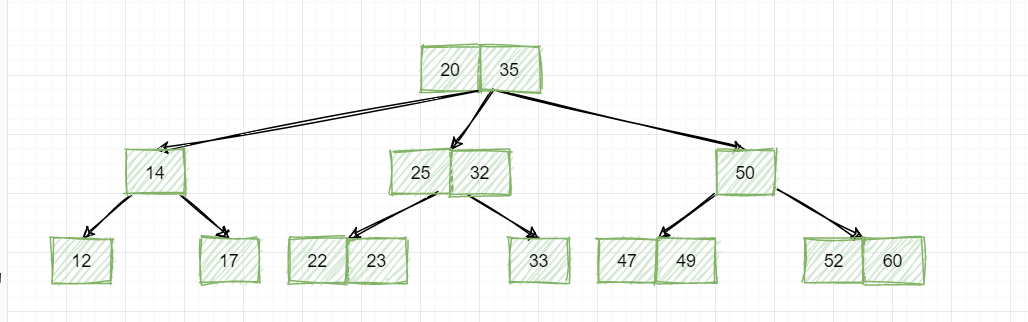
为什么？ 可能这个会让一部人感到疑惑，这不满足B树的各个条件吗？
看似满足，实则不满足，问题就出现在这个节点上：
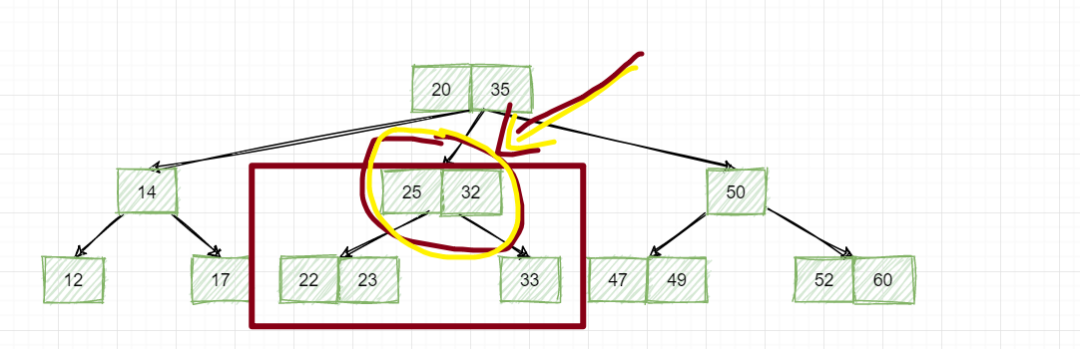
为什么？因为它含有两个数据，那么就需要有3个子节点，现在只有2个子节点，那就不满足B树！（非叶子节点，含有m个数据需要有m+1个子节点）
上面也说了，一个3阶B树其实就是一个2-3树，放在2-3树里面来说，该节点是个3-节点，那就是拥有两个数据需要三个叉！（如果是叶子节点就可以没有子节点）
所以它不满足B树或者2-树！
重点理解绝对平衡
在写这篇文章的时候，查阅了很多的资料，也看了很多网上的博客文章，但是真实越看越迷糊，越看越懵，其中很重要的一点就是发现，很多博客写的真的都是抄来抄去，甚至都没有自己的理解，就是把概念直接堆上去！
而且有的还抄错……
这里来个小插曲，重点说下我对多叉平衡树的一些重点理解，对于多叉平衡树，我这里指的就是2-3树和B树这些绝对平衡的多叉树！
重点就是要理解这里的平衡，我们之前学二叉树，可以这样：
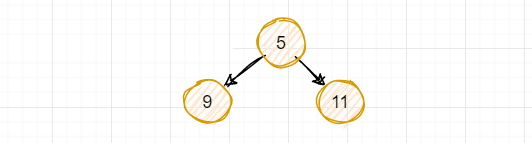
这就是一个很经典的二叉树，但是这样的二叉树用处不大，就是一个树形结构存储数据而已，而且这个二叉树还可以这样：
只是节点5没有右子树而已，但是它依然是个二叉树，后来人们想，这个二叉树的节点数值可否有顺序，这样就出来了二叉查找树，也就是这样：
比着普通的二叉树，这种二叉查找树明显多了一个条件，就是数据值有了顺序，小的都在左边，大的都在右边！
而且这棵二叉查找树还可以这样：
就是只有左子树，没有右子树，这就造成了二叉查找树的过渡左倾，所以后来想着能不能解决这种问题，就出现了二叉平衡树，也就是AVL树，后来再升级，又有了红黑树，这些都是二叉树的平衡实现！
那到了多叉树，主要是多叉平衡树，比如就拿2-3树来举例吧，首先来看一个普通的多叉树：
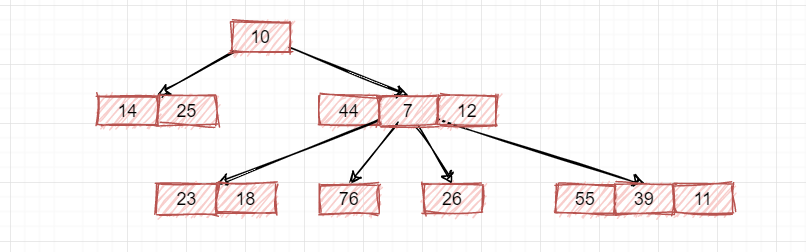
这就是一个普通的多叉树，相比较普通的二叉树，我们可以明显发现，叉变多了，一个节点保存的数据也变多了，但是同样，这样的多叉树意义不大，需要给它加上一些顺序才能发挥多叉树的好处！
首先就是数据有序，上面可以看到数据存放是比较乱的，没有顺序，所以首先数据需要有序，也就是和二叉查找树一样，左边小，右边大，依次排列，如下：
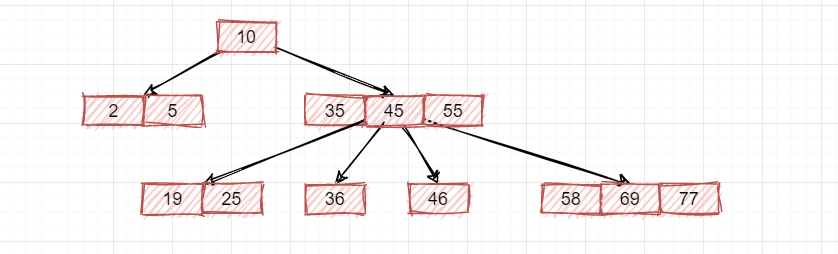
目前只是满足了数据有序，可以称之为多叉查找树了，但是这种树依然会出现左倾或者右倾的现象，就像二叉查找树，为了解决这种问题，需要平衡树的出现，也就是AVL树，规定了左右子数高度差不能大于1，以此杜绝过渡左倾和右倾，从而达到平衡！
那放到多叉树这块，就属于一种绝对平衡，不再像AVL树那样，允许左右子树高度差可以为1，多叉树的平衡，是绝对平衡，不允许有高度差，所有叶子节点必须在同一层，而且很重要的一点就是，除了叶子节点和根节点，其他节点的子树不能有所缺少，比如一个节点存储m个数据，那你就得有m+1个子节点！
如果这样的树再加以规定一个节点最多能存储2个数据，这样该节点就有3个子节点，也可以一个节点存储1个数据，那么该节点就有2个节点，前者节点成为3-节点，后者节点成为2-节点，有这样的2-节点和3-节点组成，也就成了所谓的2-3树！
按照上述规则我们再来看该树：
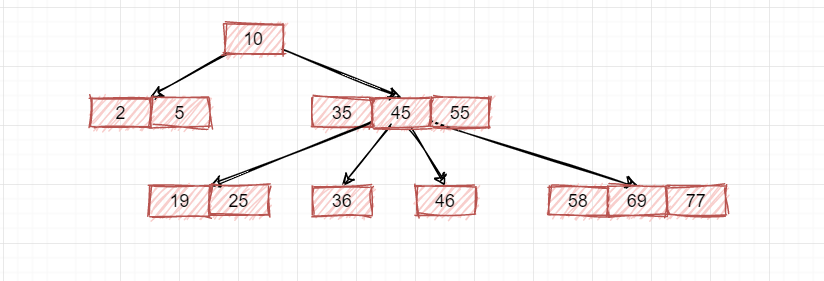
它是一棵2-3树吗？当然不是，哪里不满足了呢？
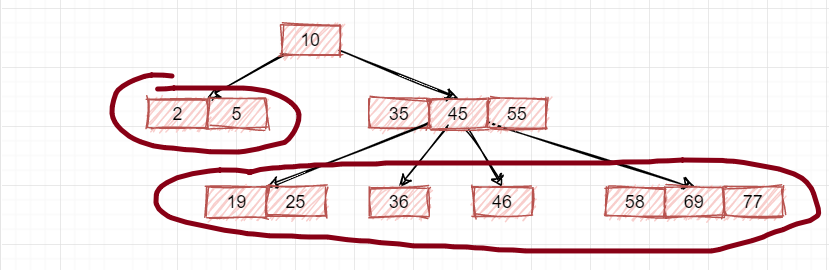
首先就是这里，即所有子节点不在同一层，修改下：
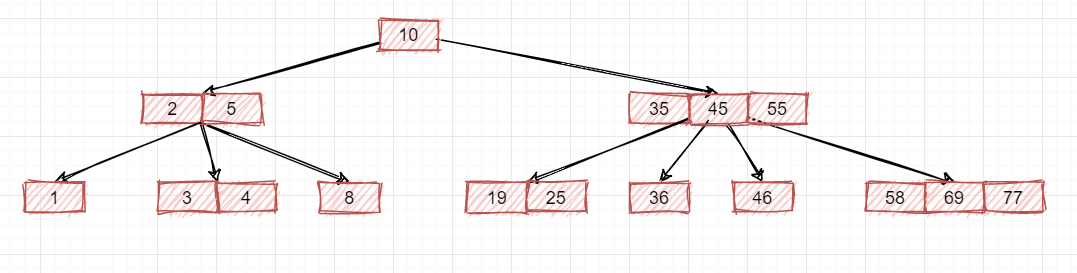也就是必须把节点（2,5）的子节点给补充出来，而且一定是三个子节点，要是如下这种就不行：
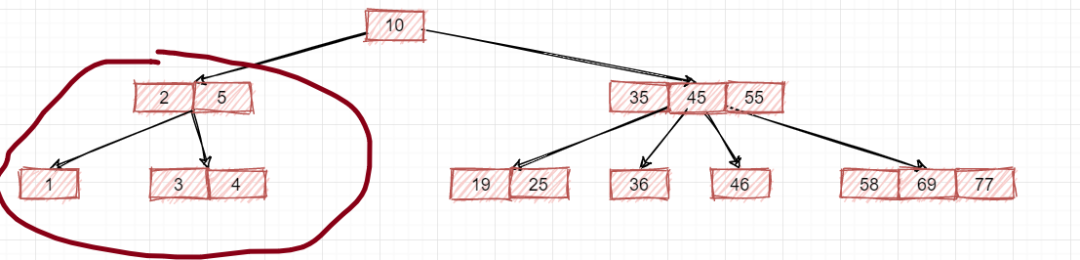
因为节点（2,5）存储2个数据，就得有3个子节点，这就是所谓的绝对平衡！但是上树此时是一个2-3树了吗？
依然不是，为什么？问题还出现在这里：
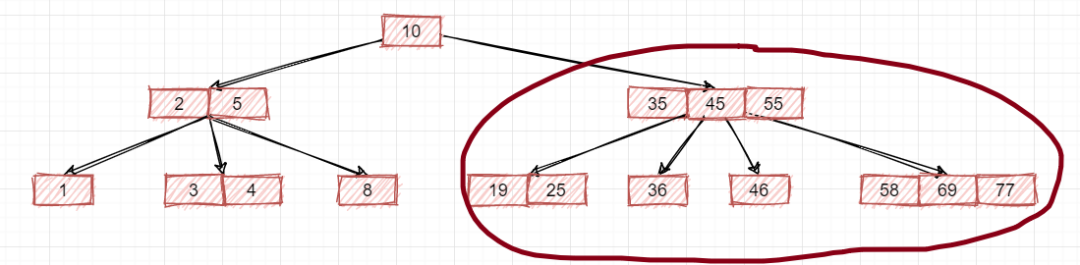怎么回事？因为这个节点含有三个数据元素，是一个4-节点，下面有四个子节点，对于一个2-3树是只能有2-节点和3-节点这两种节点的，所以要想是一个2-3树，必须该节点去除一个数据元素以及减少一个叉：
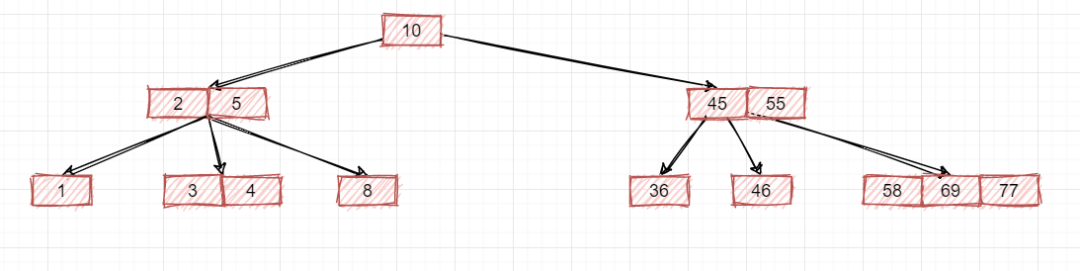修改成上述这样大家觉得这下总该是一棵2-3树了吧，很遗憾，它依然不是，问题依旧存在，就是这里：
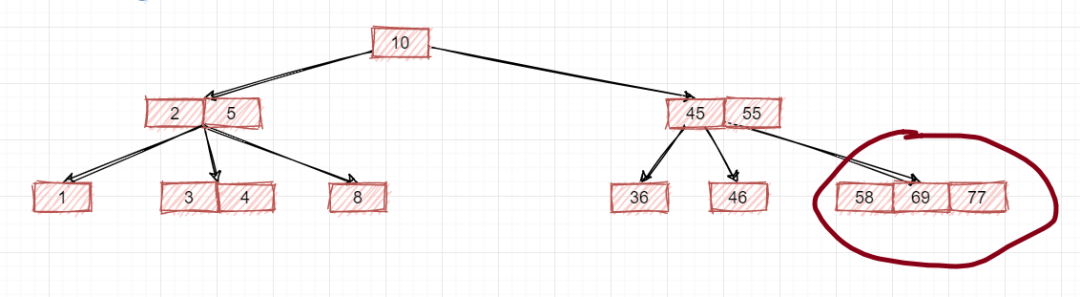其实问题是一样的，就是你既然是一棵2-3树，最大的节点是3-节点含有两个数据和三个子节点，那这里的子节点就不能含有三个元素值，最多只能俩，所以要去除一个：
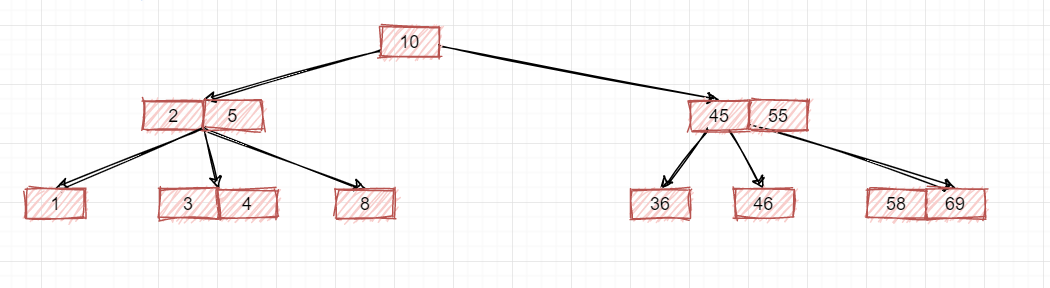
如此一来，这才是一棵真正的2-3树！
那放到B树上也是这么回事，只不过B树不限于只有2-节点和3-节点，可以有n-节点，比如B树可以存在一个5-节点，也就是该节点有5个叉，节点数据呢？一定是4个数据，如果该节点的叉最多，那该B树就成为5阶B树！
**特别注意：**比如这棵5阶B树，我们知道，一个节点的元素最多是4个数据，那最少呢？一个可以不，答案是不可以，最少要有(5/2)-1个，也就是2个！
所以说，2-3树就是一棵B树，还是一棵3阶B树，因为2-3树最多的叉就是3-节点拥有的三个叉！所以2-3树其实就是一棵3阶B树！
因此到了这里，大家就要明白像2-3树和B树的平衡是怎么回事，为什么说是绝对平衡，这块是理解学习多叉平衡树的关键！
B树的操作
B树查找
下面来看下关于B树的查找，其实查找一定是最简单的，因为查找操作不会破坏平衡，继续看如下这棵B树：
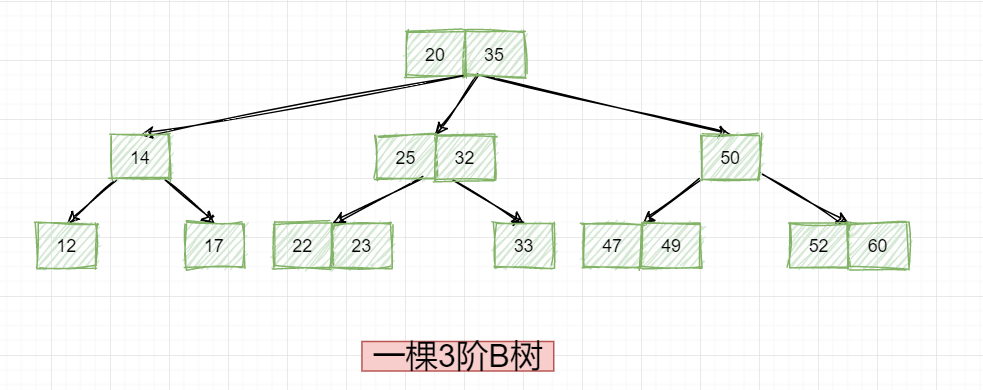
比如我们要查找数据33，怎么查找，有这么三步步骤，大家可以看一下：
1、首先在节点内部从小到大搜索该元素，刚开始就是从根节点开始了
2、接着，如果成功查找到元素就结束，没有的话，根据元素大小去该节点的对应子节点中去查找
3、如果查找到就结束，没有的话继续去对应子节点中查找
以上面的3阶B树为例，首先在根节点中查找：
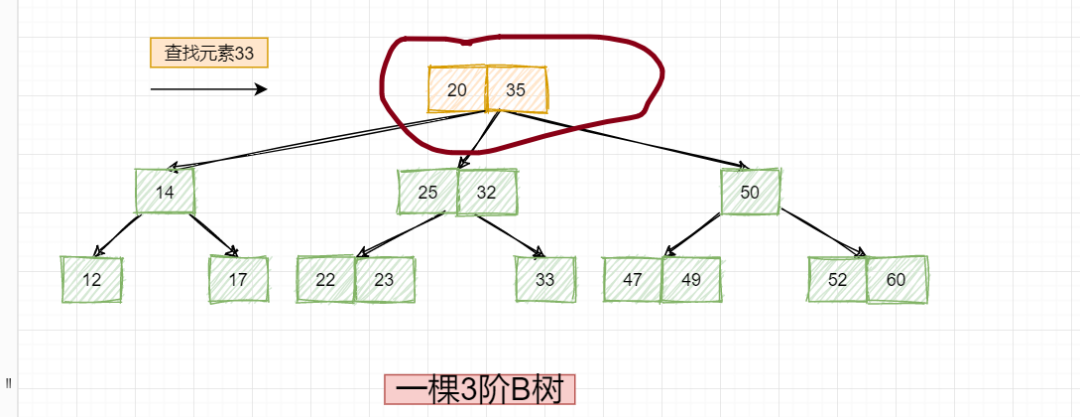
根节点没有命中，且发现33是大于20小于35的，因此去其中节点查找：
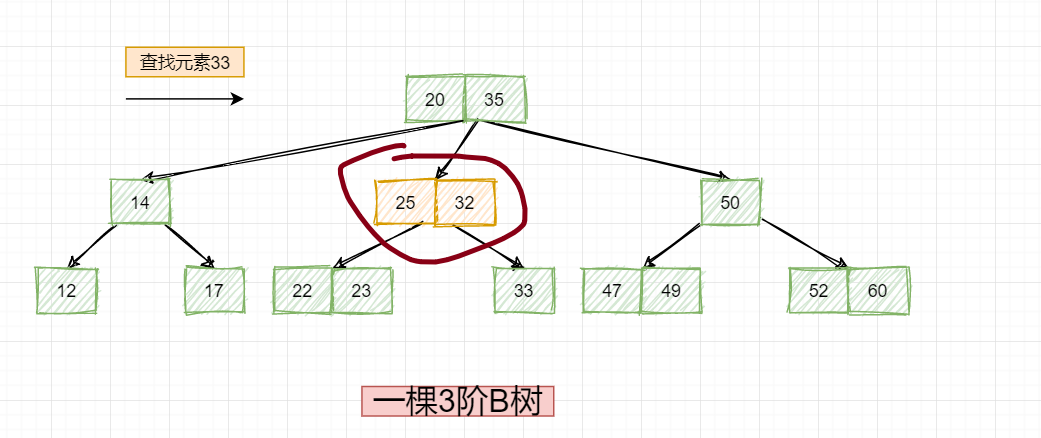依然没有命中，然后发现，要查找的元素是大于32的，所以去该节点的右子树查找：
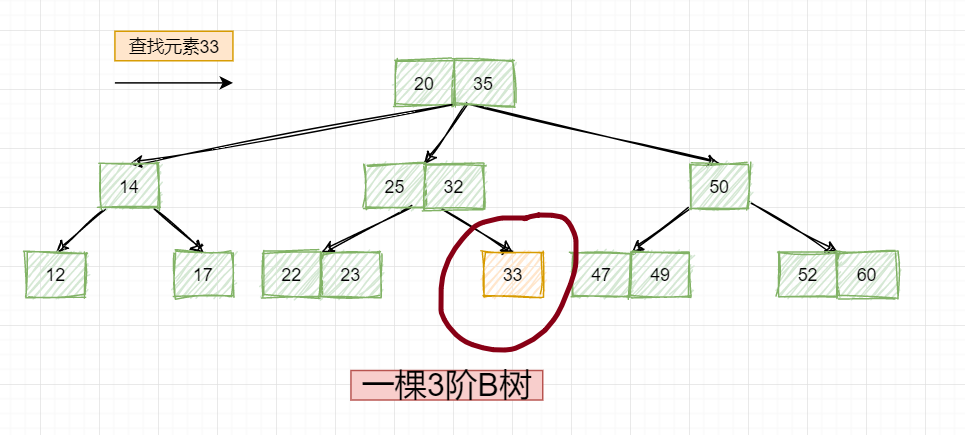
成功查找到该元素！
B树添加
接着我们再来看B树的添加操作！还是以这棵3阶B树为例：
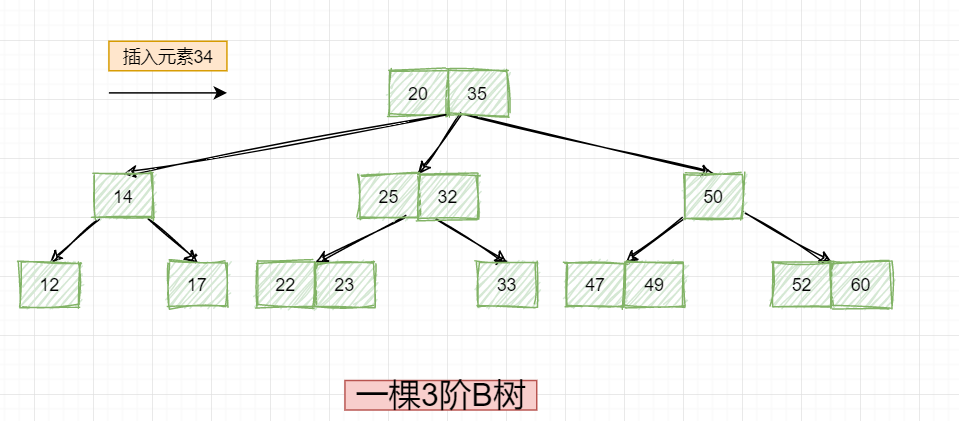
比如现在我们要插入一个新的元素34，该怎么插入？首先要知道的一点就是：
对于B树的添加，新插入的元素一定是添加到叶子节点上的
想一下为什么？其实也很简单，就是因为B树的绝对平衡，本身B树是平衡的，新插入的元素如果添加到非叶子节点的话一定会破坏平衡，思考一下是不是？
所以对于B树的添加，如果你要添加一个新元素，最终这个新元素的位置一定是在叶子节点上！，比如我们添加新元素34，首先是与根节点的两个元素比较：
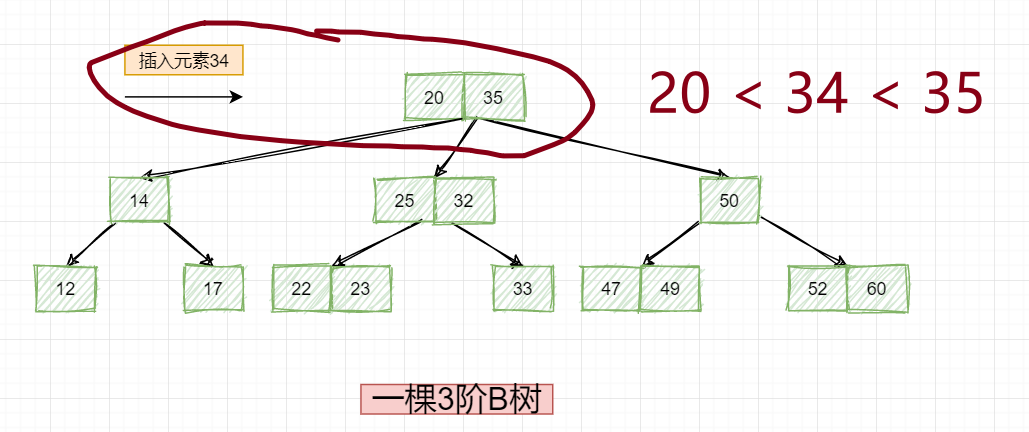
因此，就要把34添加到该节点的中节点去：
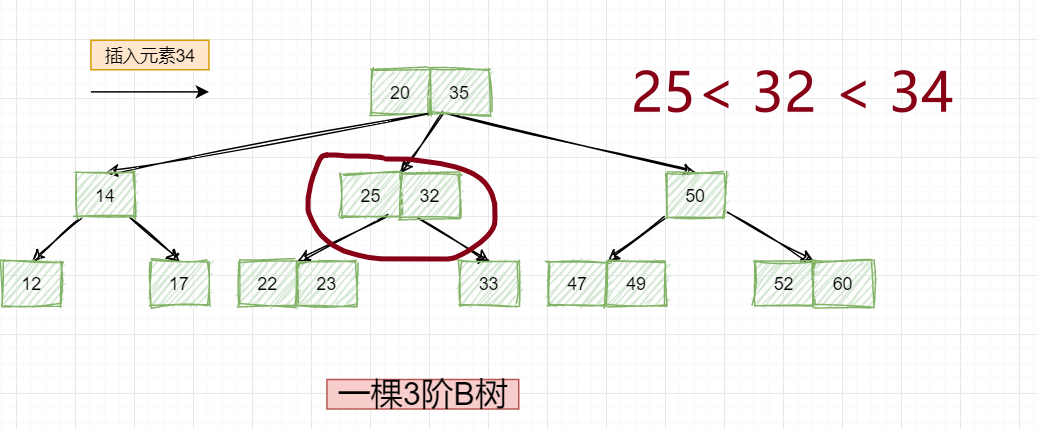
由此得出，就需要将34添加到该节点的右节点上，发现是叶子节点33，直接和33存储在一起并且在其右边：
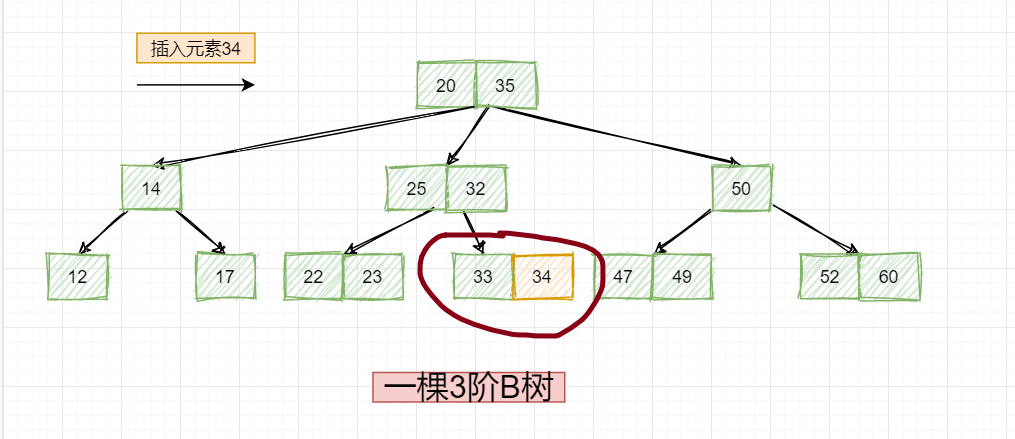
接下来我们再来看一种情况，加入现在我们继续添加元素66，该怎么办？有人说，简单啊，最终不是这样吗？
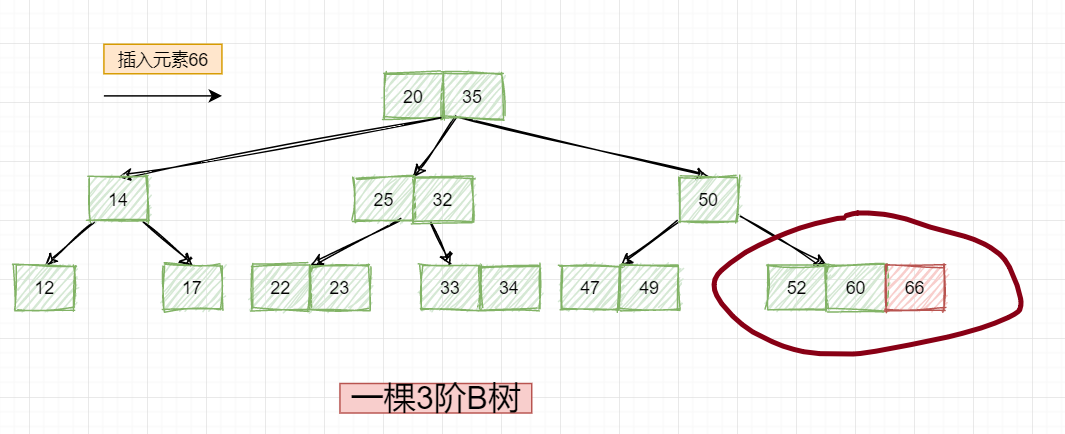
我就想问一下，这样对吗？其实是不对的？为什么？
要注意，我们上面说了这是一棵什么树，是3阶B树，那什么是3阶B树，是不是就是一个节点最多2个元素然后含有三个叉，但是上述添加之后该节点就保存了3个元素，这就不是一棵3阶B树了！
这种情况是一定要注意的，那怎么办？其实也简单，大家直接看平衡后的情况：
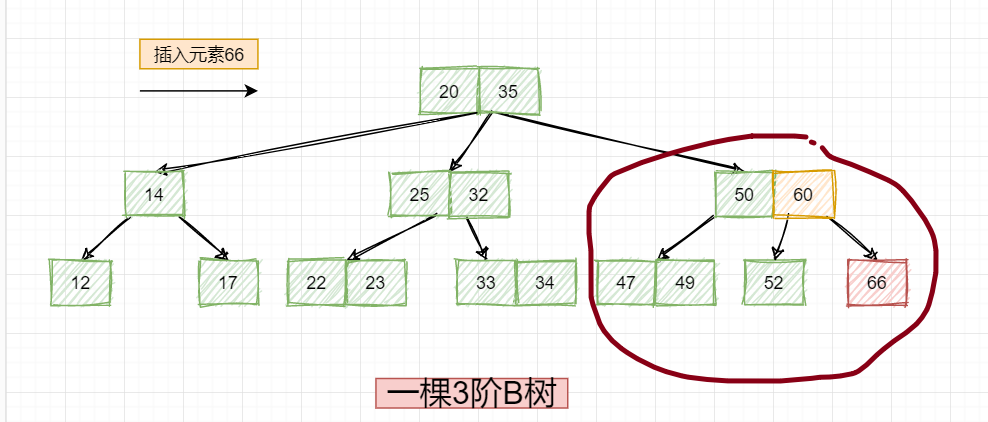
发现没有，其实就是将添加候不符合的节点给进行拆分，这里不符合的就是该节点：
我们找出该节点的中间元素也就是60，将其与父节点合并，然后该节点剩下的数值正好分裂成两个子节点，也就成了这样：
ok，到了这里我们再看一个更加复杂的插入情况，假如现在我要继续插入新的元素48该怎么办？一定要注意咱们的前提，是一棵3阶B树，我这里直接给出最后的插入情况：
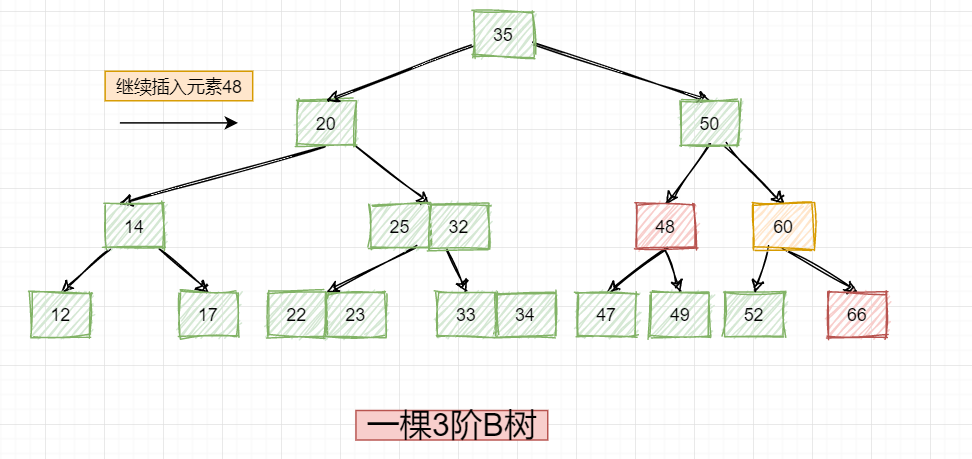
最后就成了上述这样，可以看到，最终会上升到根节点的分裂，一旦对根节点分裂拆分就会大致整体树高增加1，上述的情况大家自己要自己整理清楚，知道插入48以后的拆分情况！
B树的删除
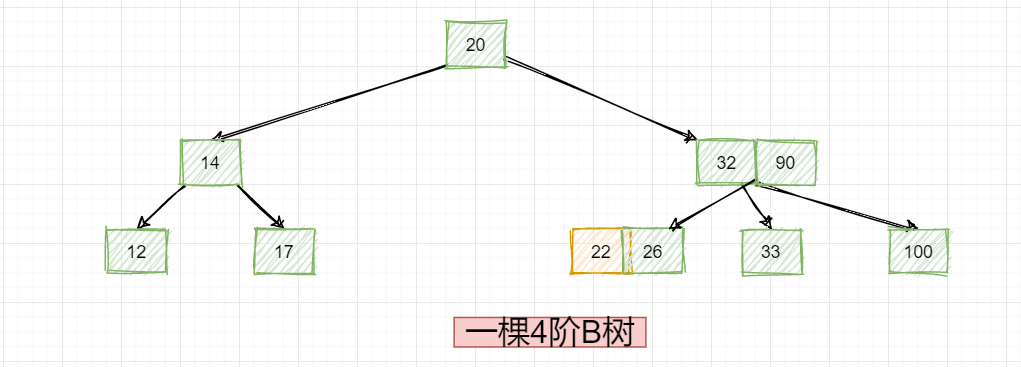
接下来我们再来看看B树的删除，首先最简单的情况就是删除的数据在叶子节点，这样的话就可以直接删除，比如下面这个4阶B树：
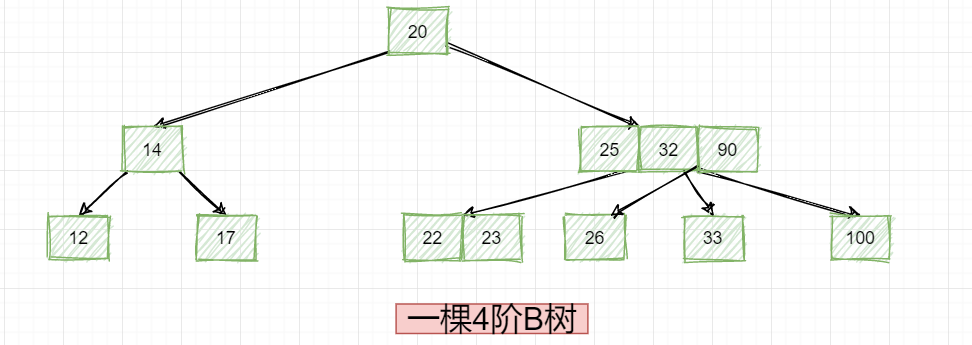
如果我们要删除数据23的话，可以直接删除即可，如下：
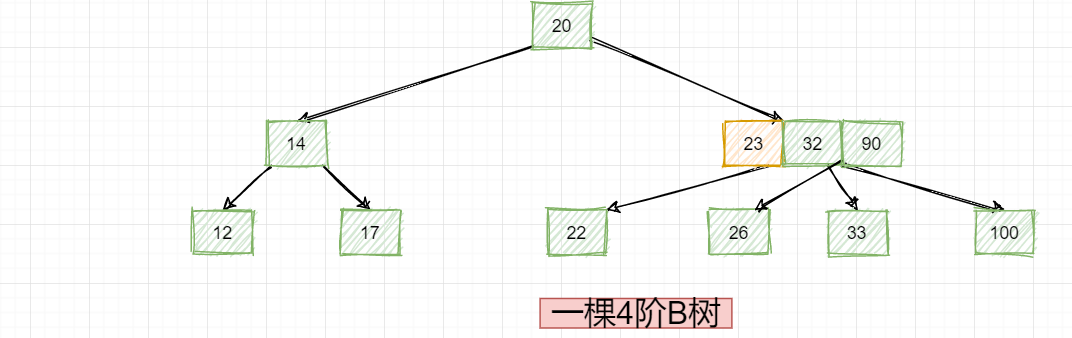
但是如果我们要删除数据25的话会怎样？同样要考虑一个前提就是这棵树是一个4阶B树，一旦删除数据25的话，B树就不平衡了！再看下这个树：
如果删除25，那该怎么办？其实也简单，核心就是：
找到要删除节点的前驱或者后继，替换要删除的节点，然后再删除前驱或者后继
什么意思呢？我这里直接把删除后的情况展示给大家：
不知道大家发现没有，这里其实就是找到要删除的这个节点数据（25）的前驱（23）或者后继（26），然后干嘛？替换掉或者说是覆盖掉要删除的这个节点，这其实就是B树的删除，怎么样？
看懂了吗？这里是前驱进行了替换！
接下来可能有人又要说了，如果我要继续删除23该怎么办？也就是现在这种情况：
我现在要把23删除掉，这个时候要怎么操作？
要知道，删除23，如果继续前驱或者后继替换的话，也是有问题的，可以想想，这个该怎么处理？
这里做了个动画，大家可以看下：
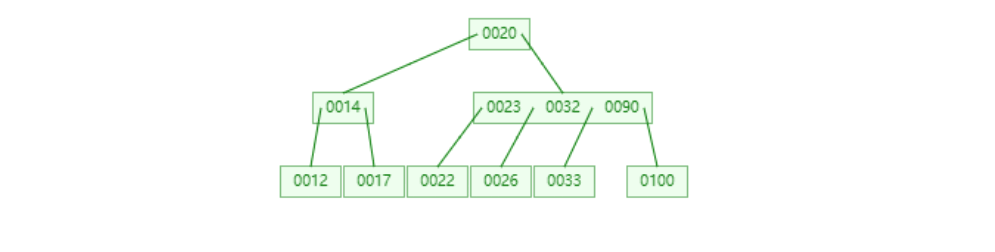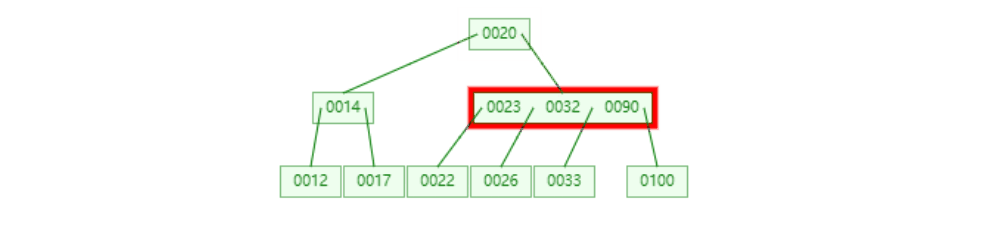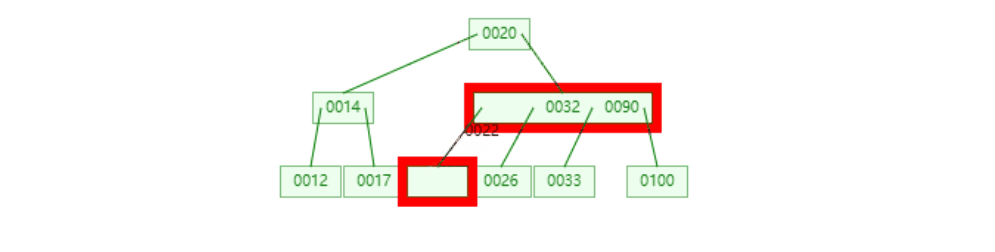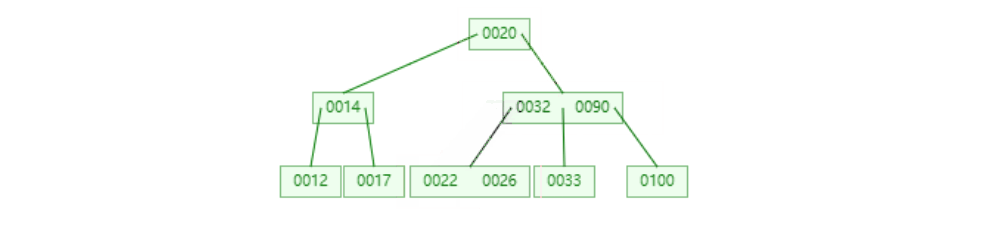然后我们一步步来解读下，首先是删除这个23，我门先找到它的前驱22，然后替换掉23：
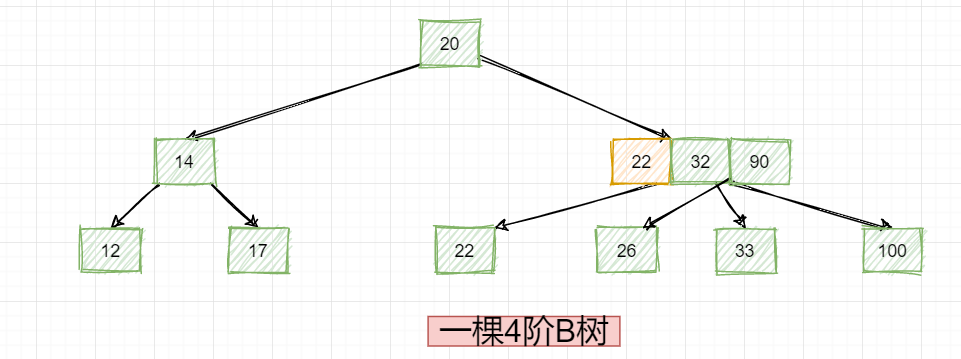接着就要把这个前驱22给删除掉：
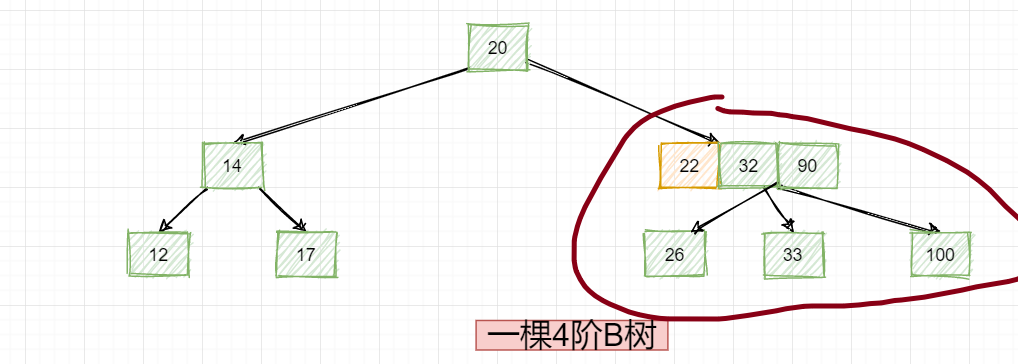
但是此时这里的节点就出问题了，怎么办，再把22拉下来与26存储到一起：
如此一来就完成了删除操作！
接下来，我们再来看看删除的另外一种情况，这次换一棵5阶B树：
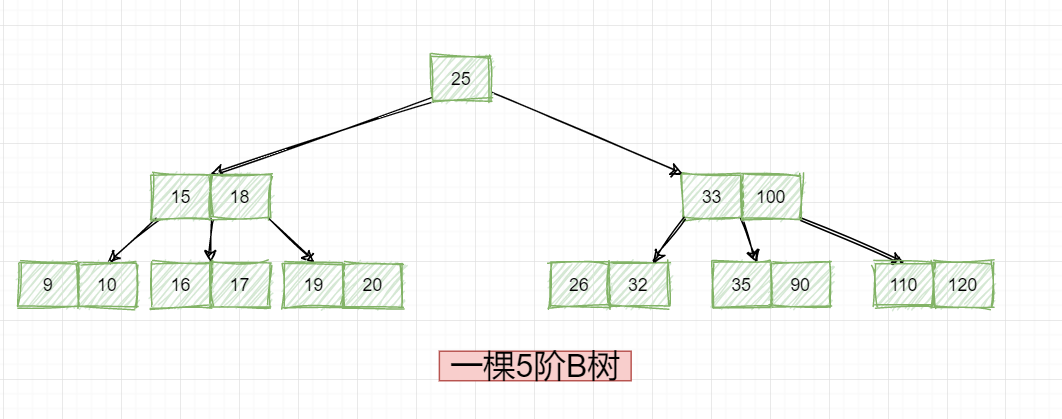记住前提，这是一棵5阶B树！如果这个时候我要删除19该怎么办？有人可能要说，这是删除的叶子节点数据，直接删除不就行了？当然不行，为什么，已经说了这是一棵5阶B树，那作为一棵5阶B树，节点数据个数有什么要求？
是不是要符合：
一棵m（>=2）阶的B树，非根节点的数据元素个数为x，则(m/2)-1 <= x <= m-1（m/2 向上取整，比如3/2 结果是2）
也就是说，这棵5阶B树节点数据个数最少要有2个！所以删除19不平衡了！
**怎么办？**我们一步步来分析，首先是删除这个19：
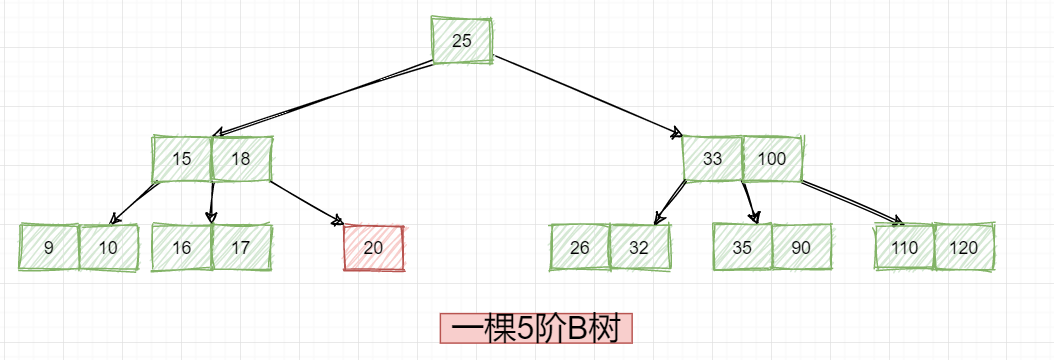此时20孤立无援了，因为必须包含两个数据，此时20就它自己，咋办，这里有两个方法：
1、借：也就是向临近兄弟节点借一个满足最低要求 2、合并：如果兄弟节点刚好2个，肯定不会借给你，这个时候只有与其合并了
比如上面的情况，20孤立无援，向旁边的节点借一个？不行吧，16和17人家刚好俩，这个时候咋办，只能合并，也就是这样：
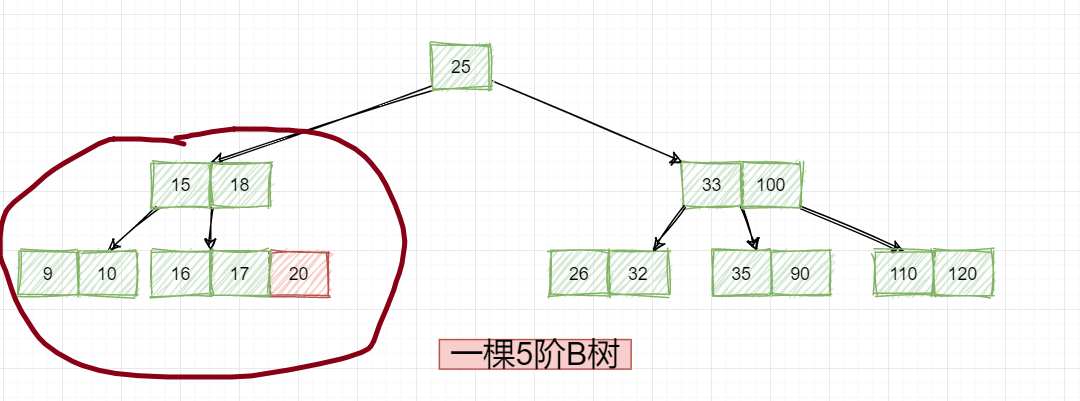
但是此时也有问题啊，节点（15，18）应该三个子节点，现在只有两个，咋整：
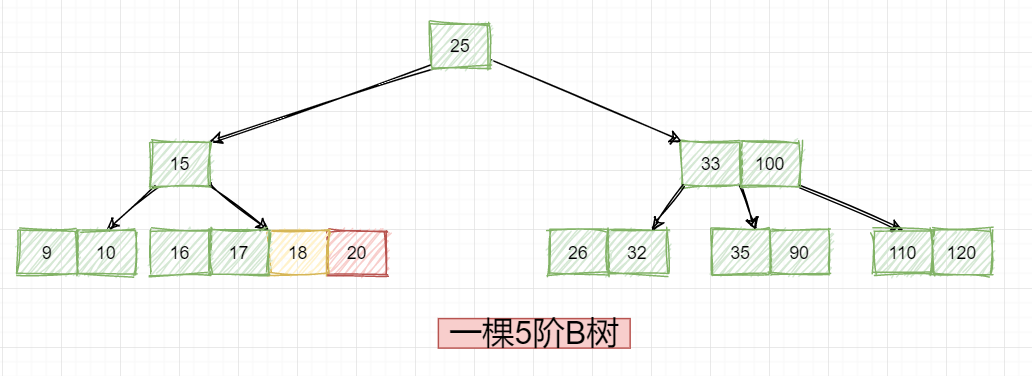这个时候就得把18拉下去合并，此时节点15又孤立无援了，咋整？此时很容易想到，把根节点25拉下来一起合并如下：
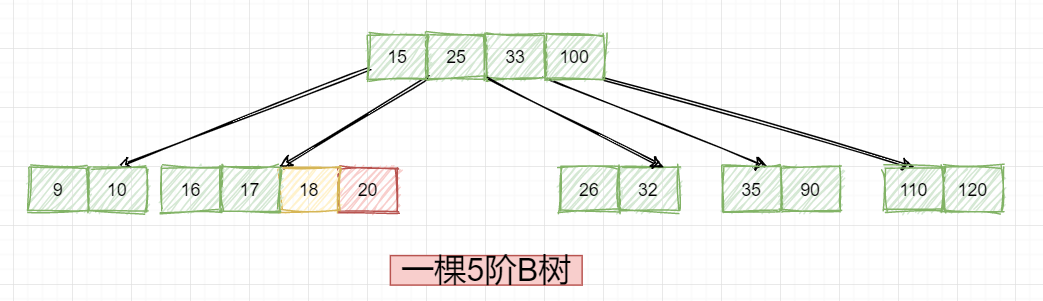
ok，到了这里就把B树的一些简单操作给大家介绍了下，那关于B树的知识，我们就暂且介绍到这里！
本文选自付费手册《数据结构》，想学习完整的数据结构知识，可订阅该专栏，提供答疑，不断更新，感兴趣的可以看看，均为庆哥原创！