原理+代码｜Python实现 kmeans 聚类分析
01
前言
聚类分析是研究分类问题的分析方法，是洞察用户偏好和做用户画像的利器之一，也可作为其他数据分析任务的前置探索(如EDA)。上文的层次聚类算法在数据挖掘中其实并不常用，因为只是适用于小数据。所以我们引出了 K-Means 聚类法，这种方法计算量比较小。能够理解 K-Means 的基本原理并将代码用于实际业务案例是本文的目标。下文将详细介绍如何利用 Python 实现基于 K-Means 聚类的客户分群，主要分为两个部分：
详细原理介绍 Python代码实战
02
原理介绍
上一篇层次聚类的推文中提到「既然它们能被看成是一类的，所以要么它们距离近，要么它们或多或少有共同的特征」。为了能够更好地深入浅出，我们像上次那样调整一下学习顺序，将数学公式往后放，先从聚类过程与结果入手。注意，本文先以样本之间的距离为聚类指标。
K-Means 聚类的目标就一句话「将 n 个观测数据点按照一定标准划分到 k 个聚类中」。至于这个标准怎么定夺以及如何判断聚类结果好坏等问题，文章后半段会提及。
K-Means 聚类的步骤用这一张图就可以表达出来。（这里的 k 为 2，即分成两类）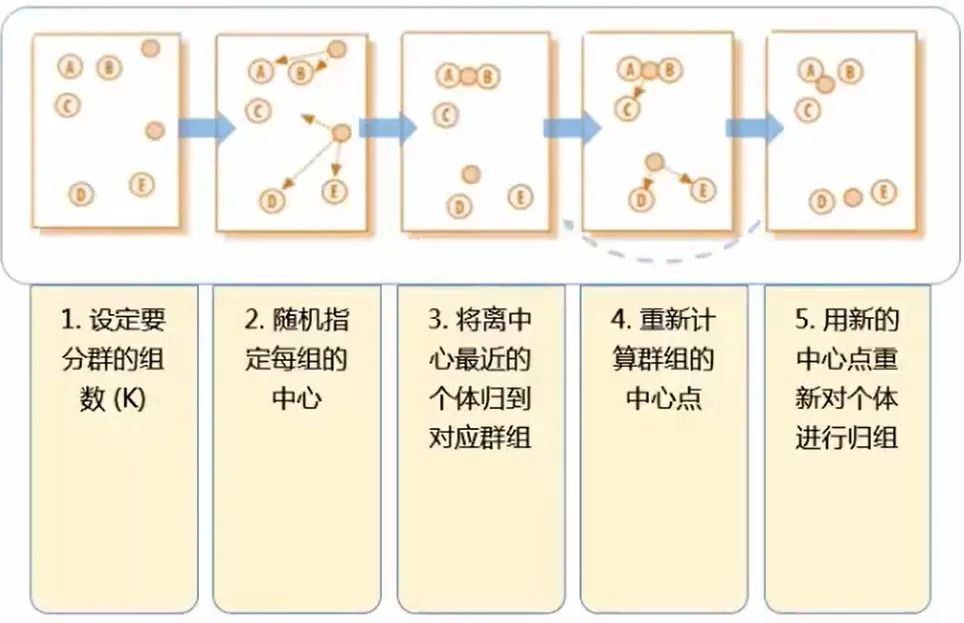
2.1 关于kmeans的一些问题
问：在第二步的随机指定每组的中心 这个步骤中，明摆着 ABC 为一类，DE 为一类 才是最正确的分类方式，毕竟肉眼就可以判断距离了，为什么指定每组的中心后反倒分类错误了呢？（第二步是将 AB 一类，CDE 一类）？
答：别着急，K-Means 算法并不求一步就完全分类正确。第二步到第三步的过程被称为“中心迭代“。一开始是随机的指定每组的中心，这个中心可能是有偏颇的，所以第三步是用每个类的中心来代替第二步中随即指定的中心。接下来再计算每个点到中心的距离，就会发现 C 这个点其实是离上面的中心更近（AB 一类，DE 一类本来就分类正确了，只是 C 出现了分类失误）
问：图中经过第四步后其实就已经划分出了正确的分类，第五步还有什么用呢？
答：第四步到第五步这个过程跟第二到第三步一样，也叫 “ 中心迭代 ”，即将新分好的正确的类的中心作为群组的中心点。这样才能为下一步的分类做准备，毕竟数据量并不只是图中的五个点，这一套(五步)流程也不是只运行一次就能完成分类，需要不断重复，最终的结果便是不会再有点像 C 那样更换分类的情况。
问：第一步要计算几次距离？（k=2）
答：需要计算 10 次距离，随即指定的两个中心点到每一个已知点的距离：中心1，2 分别到点 ABCDE 的距离。其实也就是 n 个点，分成 k 类时，需要计算 n×k 次。
问：第一步用层次聚类法也是 10 次，为什么还说 K-Means 是一个计算量较小的方法呢？
答：对第一步使用层次聚类法的计算次数为：Cn2（（C52 = (54)/2）），即计算两两点之间的距离，然后再比较筛选，即：n(n-1) / 2 = 54 / 2 = 10 次，但这只是小的数据样本，如果样本量巨大呢（同样还是 k 为 2 时）？那么 K-Means 的 n*k 与层次聚类法的 Cn2 的复杂度图比较便是：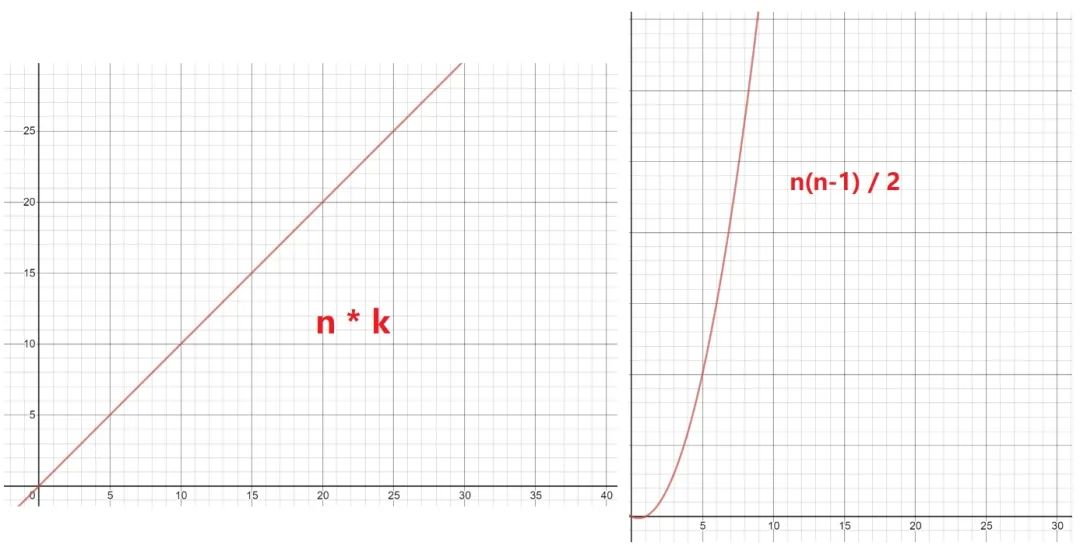
数据量一旦开始增加，层级聚类法的计算复杂程度便呈指数级增长。
问：K-Means 的不足？
答：K-Means 最显著的缺点便是 k 的个数不好确定，但在商业数据挖掘上，这个缺点其实不一定难避免。因为商业数据挖掘的 k-means 聚类方法中，k 大部分都在 2 ~ 12 这个范围，所以只需要做 9 次，然后看哪种效果最好即可。
2.2 K-Means 的要点
要点1：预先处理变量的缺失值、异常值 要点2：变量标准化 要点3：不同维度的变量，相关性尽量低 要点4：如何决定合适的分群个数？·
主要推荐轮廓系数（Silhouette Coeficient），并结合以下注意事项：
分群结果的稳定性
重复多次分群，看结果是否稳定
分群结果是否有好解释的商业意义
也有一种相对没那么严谨的分类方法，这种方法通常会分 5~8 类，这样既能反映工作量（给领导看），又不至于太累（分出 12 类，还要对每一类的特征进行探索，描述性统计分析等）
2.3 轮廓系数
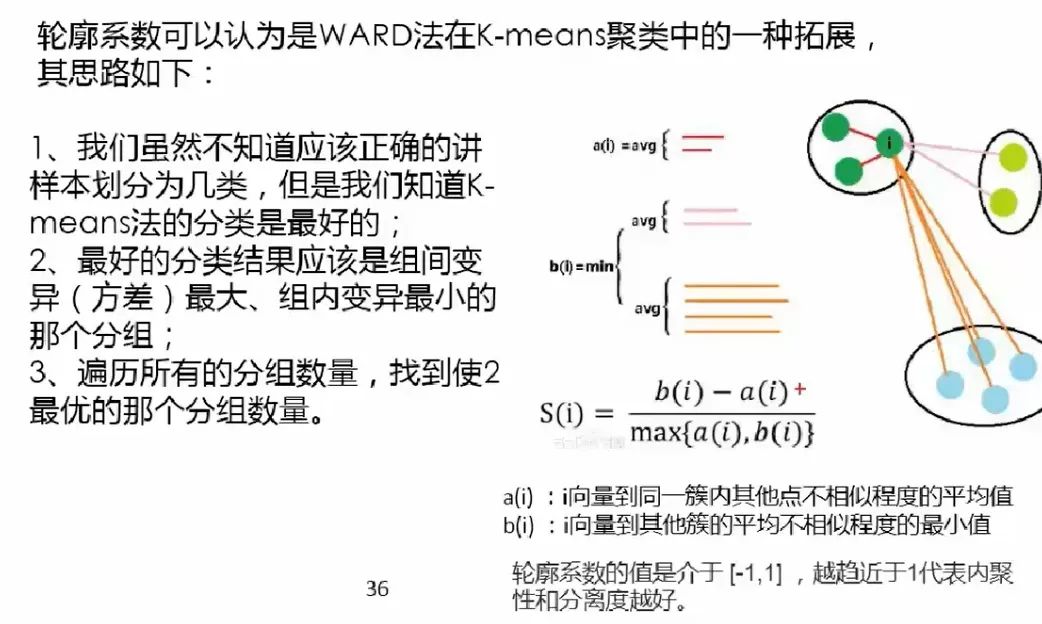
最好的分类结果：不同组之间的差距越大越好，同组内的样本差距越小越好。这样才能更好的体现物以类聚的思想（e.g: 同一类人的三观非常一致，不同类的人之间三观相差甚远）。因为组内差异为零的话，a(i) 便无限接近于0，公式分子便为 b(i)，分母 max{0, b(i)} = b(i)，所以结果为 b(i) / b(i) = 1，即越趋近于 1 代表组内聚类性和组间的分离度越好。
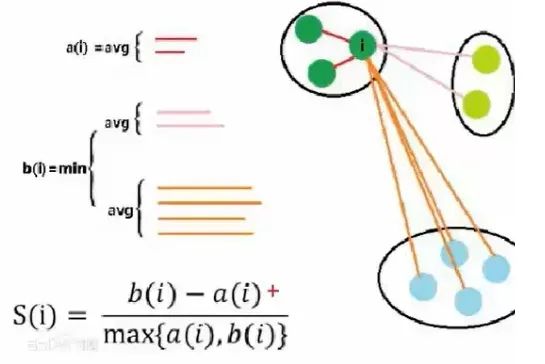
轮廓系数其实非常难求，组内的(a(i))好算，b(i) 非常难计算，而且还要每个点都要同不同组里面的所有点进行计算，所以轮廓系数在实操的时候样本量的大小需要控制，一般几千就行了，几万的话就太难计算了；换言之，轮廓系数一般也是在探索的时候用，比如分层抽样后对 k 的取值进行探索。这也再次呼应了前两段提到的 K-Means 方法的 k 难以直接通过数学公式求得的的这一特点。
2.4 K-Means 聚类的两种用法
1、发现异常情况：如果不对数据进行任何形式的转换，只是经过中心标准化或级差标准化就进行快速聚类，会根据数据分布特征得到聚类结果。这种聚类会将极端数据聚为几类。这种方法适用于统计分析之前的异常值剔除，对异常行为的挖掘，比如：监控银行账户是否有洗钱行为、监控POS机是有从事套现、监控某个终端是否是电话卡养卡客户等等。
2、将个案数据做划分：出于客户细分目的的聚类分析一般希望聚类结果为大致平均的几大类，因此需要将数据进行转换比如使用原始变量的百分位秩、Turkey正态评分、对数转换等等。在这类分析中数据的具体数值并没有太多的意义，重要的是相对位置。这种方法适用场景包括客户消费行为聚类、客户积分使用行为聚类等等。
如果变量比较多比如 10 个左右，变量间的相关性又比较高，就应该做个因子分析或者稀疏主成分分析，因为 K-Means 要求不同维度的变量相关性尽量低。（本系列的推文：原理+代码｜Python基于主成分分析的客户信贷评级实战）
那如果数据右偏严重，K-Means 聚类会出现什么情况？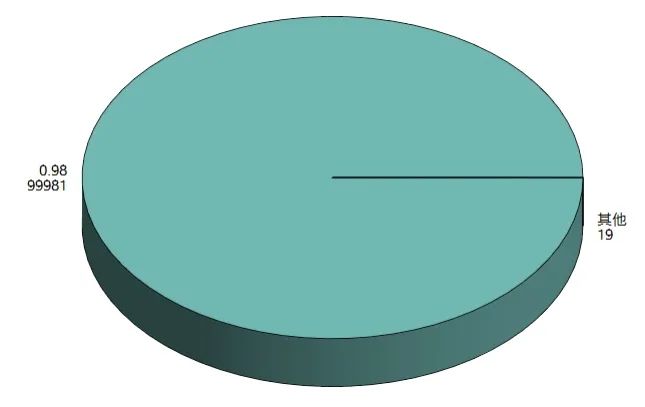
如果不经过任何处理，则聚类出来的结果便是如上图那样，出现 ”绝大部分客户属于一类，很少量客户属于另外一类“ 的情况，这就失去了客户细分的意义（除非你是为了检测异常值），因为有时候我们希望客户能够被均匀的分成几类（许多领导和甲方的需求为均匀的聚类，这是出于管理的需求）
原始数据本来就是右偏的，几种标准化方式之后其实也还是右偏的...，我们在学校学习统计学或聚类方法的时候，所用数据大多是来自自然科学的，所以分布情况都比较“完美”，很少出现较强的偏态分布。而现实生活与工作中的数据，如金融企业等，拿到的数据大多右偏严重。
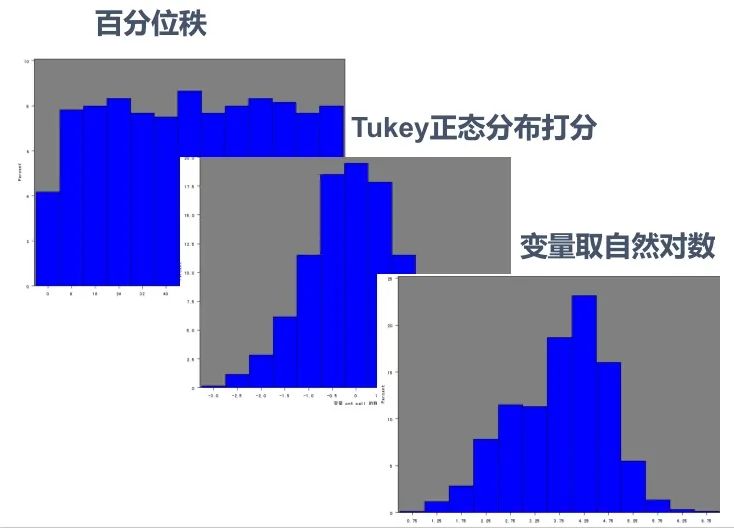上图是能够强迫将右偏数据转换成均匀分布的几种方法。但通常回归算法时的右偏处理才会使用变量取自然对数的方法，聚类算法常用 Tukey 正态分布打分的方式来处理右偏数据。
2.5 变量转换小结
非对称变量在聚类分析中选用百分位秩和Tukey正态分布打分比较多；在回归分析中取对数比较多。因为商业上的聚类模型关心的客户的排序情况，回归模型关心的是其具有经济学意义，对数表达的是百分比的变化。
2.6 使用决策树做聚类后的客户分析
聚类算法还能与决策树算法一起用（期待脸(☆▽☆)）？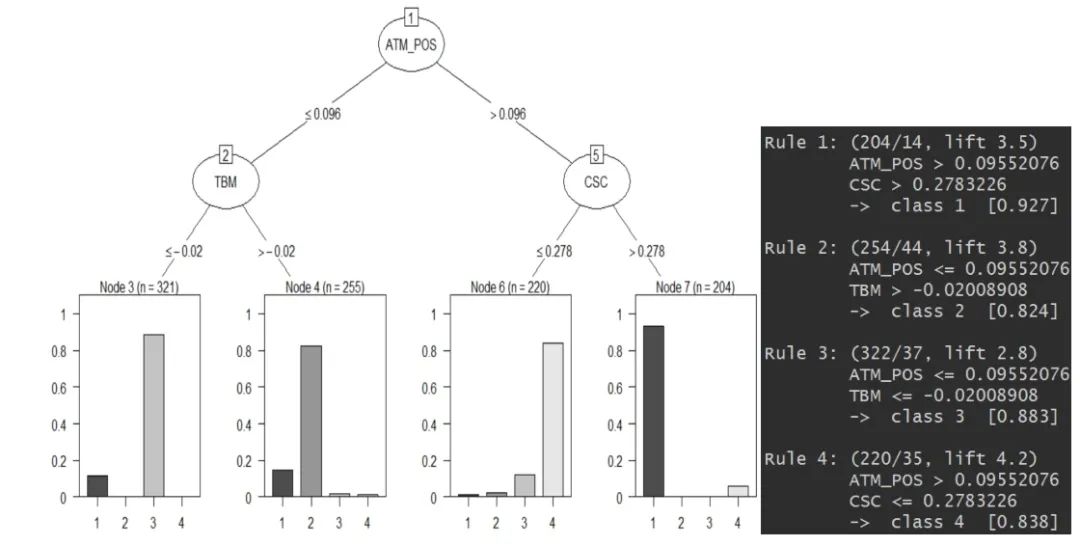
轮廓系数可以为我们做 K-Means 聚类的时候提供一个 k 的参考值，而初步聚类后，我们便有了 Y，即每个数据样本所对应的类别。这时候我们画棵决策树（可以结合使用高端一些的决策树可视化方式），如果底端的叶子所呈现出的数据分类是某一类较多，其余类偏少，这样便表示这个 k 值是一个比较好的选择。（每一类都相对较纯，没有杂质）
03
代码实战
本次代码实战我们将使用已经经过前文主成分分析处理过的有关银行客户的数据集：
CSC：counter service for customer -- 选择柜台服务的客户 ATM_POS: 使用 ATM 和 POS 服务的客户 TBM：选择有偿服务的客户
import pandas as pd
# df 为清洗好的数据
df = pd.read_csv('data_clean.csv')
df.head()
这里每个变量所在列的具体数值可先不做探究
这里每个变量所在列的具体数值可先不做探究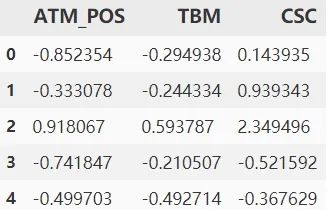
3.1 K-Means 聚类的第一种方式
不进行变量分布的正太转换--用于寻找异常值
# 使用k-means聚类
## 1.1 k-means聚类的第一种方式：不进行变量分布的正态转换--用于寻找异常值
# 1、查看变量的偏度
var = ["ATM_POS","TBM","CSC"] # var: variable-变量
skew_var = {}
for i in var:
skew_var[i]=abs(df[i].skew()) # .skew() 求该变量的偏度
skew=pd.Series(skew_var).sort_values(ascending=False)
skew
可以看出 TBM 这个变量的偏度已经超标，很可能会影响到后续的分类
进行k-means聚类
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3) # n_clusters=3 表示聚成3类
result = kmeans.fit(df)
result
与随机森林，决策树等算法一样，KMeans 函数中的参数众多，这里不具体解释了，可查阅官方文档
.join() 表示横向拼接
# 对分类结果进行解读
model_data_l = df.join(pd.DataFrame(result.labels_))
# .labels_ 表示这一个数据点属于什么类
model_data_l = model_data_l.rename(columns={0: "clustor"})
model_data_l.sample(10)
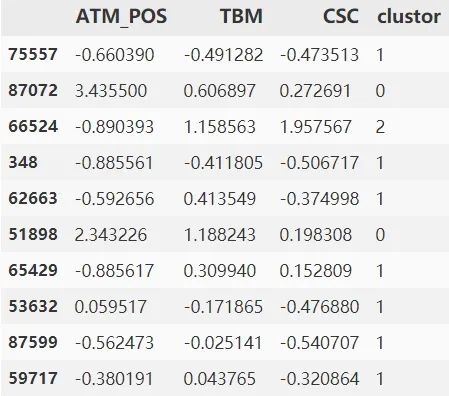绘制饼图呈现每一类的比例
# 饼图呈现
import matplotlib
get_ipython().magic('matplotlib inline')
model_data_l.clustor.value_counts().plot(kind = 'pie')
# 自然就能发现出现分类很不平均的现象
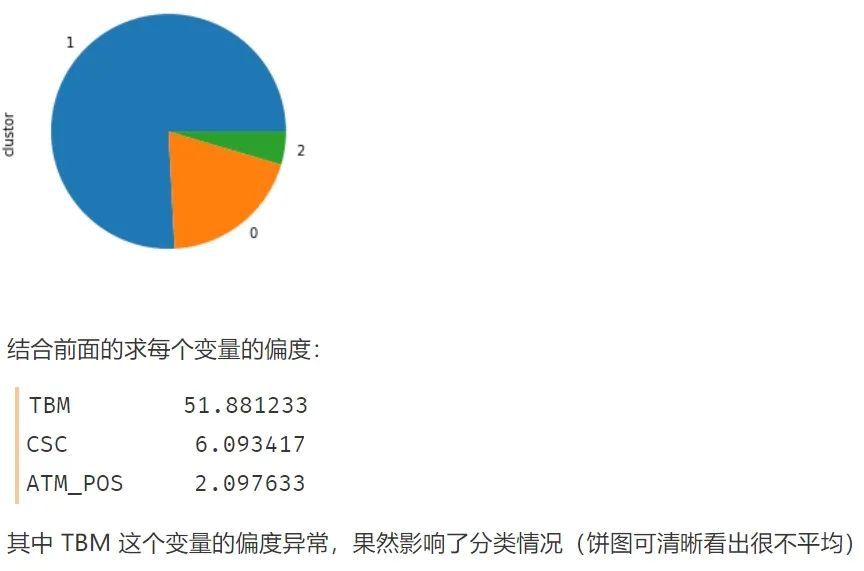
3.2 k-means聚类的第二种方式
进行变量分布的正态转换--用于客户细分
# 进行变量分布的正态转换
import numpy as np
from sklearn import preprocessing
quantile_transformer = \
preprocessing.QuantileTransformer(output_distribution='normal',
random_state=0) # 正态转换
df_trans = quantile_transformer.fit_transform(df)
df_trans = pd.DataFrame(df_trans)
# 因为 .fit_transform 转换出来的数据类型为 Series，
## 所以用 pandas 给 DataFrame 化一下
df_trans = df_trans.rename(columns={0: "ATM_POS", 1: "TBM", 2: "CSC"})
df_trans.head()
转换的方式有很多种，每种都会涉及一些咋看起来比较晦涩的统计学公式,但请不要担心，每种代码其实都是比较固定的，这里使用 QT 转换（每种转换的原理和特点优劣等可参考网络资源）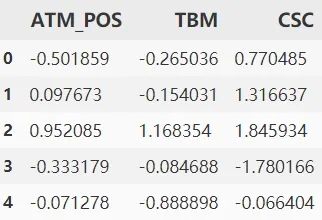
检验一下偏度：发现几乎都为 0 了
var = ["ATM_POS","TBM","CSC"]
skew_var = {}
循环计算偏度：发现都差不多等于 0 了。
for i in var:
skew_var[i] = abs(df_trans[i].skew())
skew = pd.Series(skew_var).sort_values(ascending=False)
skew # 字典显示更方便
重复的聚类步骤，代码可直接粘贴
kmeans = KMeans(n_clusters=4) # 这次聚成 4 类
result = kmeans.fit(df_trans)
model_data_l = df_trans.join(pd.DataFrame(result.labels_))
model_data_l = model_data_l.rename(columns={0: "clustor"})
model_data_l.head()
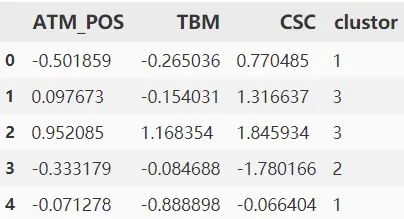再次使用饼图呈现结果，发现每类的比例开始平均了。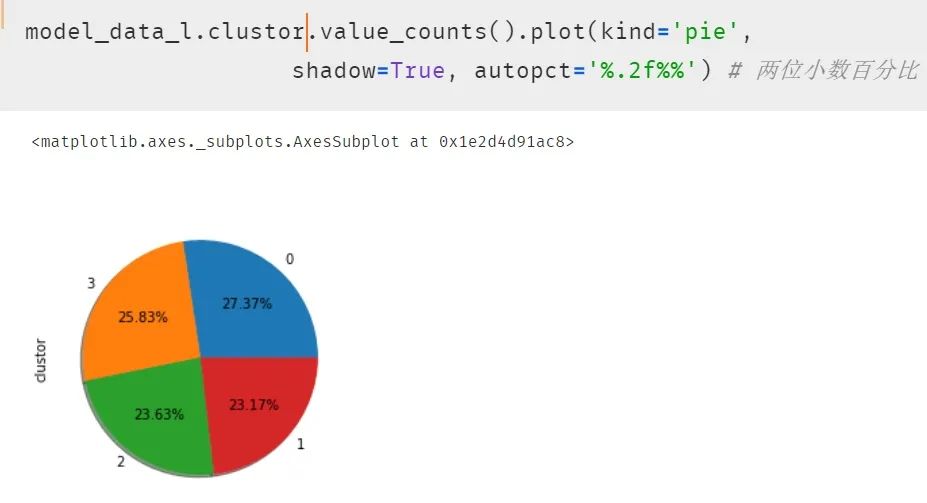
3.3 结果分析
最后对结果进行分析如下表
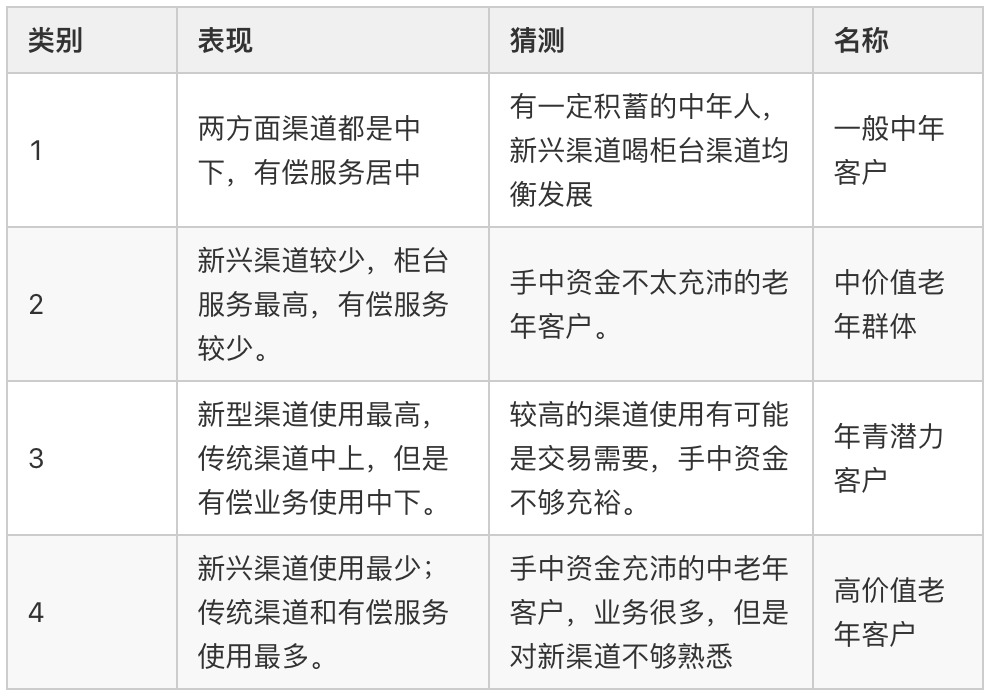
小结
对于不同场景，我们的使用聚类的方法也有所不同：
“”
一般场景下的聚类：「变量归一化 --> 分布转换 --> 主成分 --> 聚类」 发现异常境况的聚类：「变量归一化 --> 主成分 --> 聚类」
其实聚类模型对分析人员的业务修养要求较高，因为聚类结果好坏不是简单的看统计指标就可得出明确的答案。统计指标是在所有的变量都符合某个假设条件才能表现良好的，而实际建模中很少能达到那种状态；聚类的结果要做详细的描述性统计，甚至作抽样的客户访谈，以了解客户的真实情况，所以让业务人员满足客户管理的目标，是聚类的终极目标。
PS：公号内回复「Python」即可进入Python 新手学习交流群，一起 100 天计划！
老规矩，兄弟们还记得么，右下角的 “在看” 点一下，如果感觉文章内容不错的话，记得分享朋友圈让更多的人知道！
【代码获取方式】