详解全网最快 Go 泛型跳表【内附源码】
 背景
背景
最近一年我们用Go语言实现的业务系统至少70%,因此我们Review了大量的Go代码,也看了很多相关的技术资料。Go语言有两个不友好的点,一个是错误处理,另一个是泛型。我们 调研市面上是否有类似C++中STL的泛型库,结果发现它们要么很薄弱,要么根本就不支持泛型。
于是本人写了个基于泛型的容器和算法库,名为stl4go(
文末有源码链接
)。其中的有序 Map 没有选择红黑树,而是用了跳表。经过优化后,stl4go算得上是 GitHub 上能找到的、最快的 Go 实现。如果你感兴趣,欢迎继续往下阅读。
 跳表是什么
跳表是什么
跳表(skiplist)是一种 随机化的数据 , 由 William Pugh 在论文Skip lists: a probabilistic alternative to balanced trees中提出。 跳表以有序的方式在层次化的链表中保存元素, 效率和平衡树媲美——查找、删除、添加等操作都可以在O(logN)期望时间下完成, 综合能力相当于平衡二叉树。比起平衡树来说, 跳跃表的实现要简单直观得多,核心功能在200行以内即可实现,遍历的时间复杂度是O(N)。代码简单、空间节省,在挺多的场景得到应用。
SkipList用于需要有序的场合。在不需要有序的场景下,go自带的map容器依然是优先选择。

接口设计
1)创建函数
对于可以用 <、== 比较的类型,可以使用简单的创建函数。对于不可以直接比较的,也可以通过提供自定义的比较函数来创建。
// 对于Key可以用 < 和 == 运算符比较的类型,调这个函数来创建
func NewSkipList[K Ordered, V any]() *SkipList[K, V]
// 其他情况,需要自定义Key类型的比较函数
func NewSkipListFunc[K any, V any](keyCmp CompareFn[K]) *SkipList[K, V]
// 从一个map来构建,仅为方便写Literal,go没法对自定义类型使用初始化列表。
func NewSkipListFromMap[K Ordered, V any](m map[K]V) *SkipList[K, V]
2)主要方法
IsEmpty() bool // 表是否为空
Len() int // 返回表中元素的个数
Clear() // 清空跳表
Has(K) bool // 检查跳表中是否存在指定的key
Find(K) *V // Finds element with specific key.
Insert(K, V) // Inserts a key-value pair in to the container or replace existing value.
Remove(K) bool // Remove element with specific key.
还有迭代器和遍历区间查找等功能与本主题关系不大,本文略去讲述。上文, 可以看得出,它完全可以满足有序Map容器的要求。
3)节点定义
虽然不少讲跳表原理示意图会把每层的索引节点单独列出来:
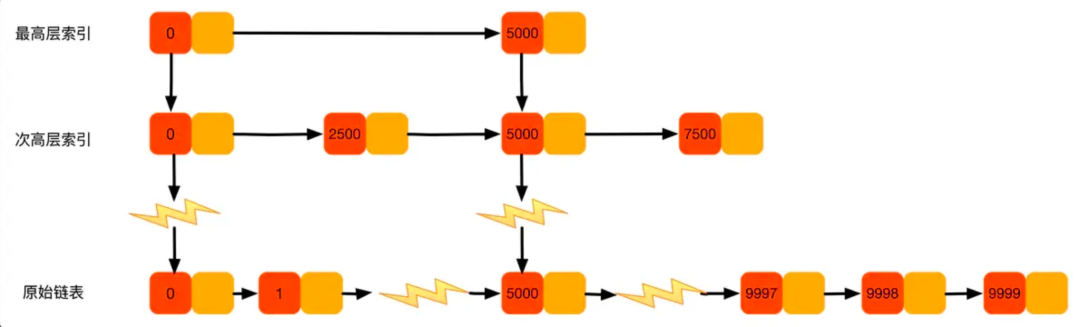
但是一般的实现都会把索引节点实现为最底层节点的一个数组,这样每个元素只需要一个节点,节省了单独的索引节点的存储开销,也提高了性能。
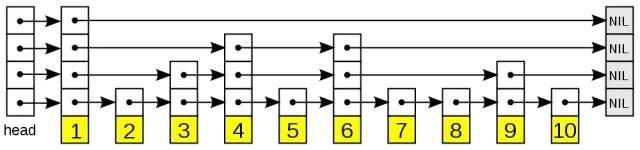
因此节点定义如下:
type skipListNode[K any, V any] struct {
key K
value V
// 指向下一个节点的指针的数组,不同深度的节点长度不同,[0]表示最下层
next []*skipListNode[K, V]
}

代码优化
代码并非完全从头开始写的,我们是以liyue201@github.com的gostl的实现为基础。其 实现比较简洁,只有200多行代码。支持自定义数据类型比较,但是不支持泛型。我们在他的基础上, 做了一系列的算法和内存分配等方面的优化,并增加了迭代器、区间查找等功能 。
liyue代码地址:https://github.com/liyue201/gostl/blob/master/ds/skiplist/skiplist.go
1)算法优化
-
生成随机Level的优化
每次跳表插入元素时,需要随机生成一个本次的层数,最朴素的实现方式是抛硬币。也就是根据连续获得正面的次数来决定层数。
func randomLevel() int {
level := 0
for math.Float64() < 0.5 {
level++
}
return level
}
Redis里的算法类似,只不过用的是1/4的级数差,索引少一半,可以节省一些内存,源代码如下:
https://github.com/redis/redis/blob/7.0/src/t_zset.c#L118-L128
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned. */
int zslRandomLevel(void) {
static const int threshold = ZSKIPLIST_P*RAND_MAX;
int level = 1;
while (random() < threshold)
level += 1;
return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
上述方法简单直白,但是存在两个问题:
第一,math.Float64() (以及任何全局随机函数)内部为共享的随机数生成器对象,每次调用都会加锁解锁,在竞争情况下性能下降很厉害。第二,多次生成随机数。看完下文你会发现,只用生成一次就可以。详情参见源代码如下:
https: //cs.opensource.google/go/go/+/refs/tags/go1.19:src/math/rand/rand.go
所以我们在gostl的实现中改用了生成一个某范围内的随机数。根据其均匀分布的特点来计算level:
func (sl *Skiplist) randomLevel() int {
total := uint64(1)<<uint64(sl.maxLevel) - 1 // 2^n-1
k := sl.rander.Uint64() % total
levelN := uint64(1) << (uint64(sl.maxLevel) - 1)
level := 1
for total -= levelN; total > k; level++ {
levelN >>= 1
total -= levelN
}
return level
}
这段for循环有些拗口,改写一下就更清晰了:
level := 0
for k < total {
levelN >>= 1
total -= levelN
level++
}
也就是生成的随机数越小则level越高。比如maxLevel为10时,total=1023,那么:
512<k<1023之间的概率为1/2,level=1
256<k<511之间的概率为1/4,level=2
128<k<255之间的概率为1/8,level=3
...
当level比较高时,循环次数就会增加 。不过,我们可以观察到在生成的随机二进制中,数值增减一半正好等于改变一个bit位。因此我们改用直接调用math/bits里的Len64()函数,来计算生成的随机数的最小位数的方式来实现:
func (sl *SkipList[K, V]) randomLevel() int {
total := uint64(1)<<uint64(skipListMaxLevel) - 1 // 2^n-1
k := sl.rander.Uint64() % total
return skipListMaxLevel - bits.Len64(k) + 1
}
而Len64函数是用查表实现的,相当的快:
https://github.com/golang/go/blob/go1.19/src/math/bits/bits.go#L330-L345
// Len64 returns the minimum number of bits required to represent x;
// the result is 0 for x == 0.
func Len64(x uint64) (n int) {
// ...
return n + int(len8tab[x])
}
当level>1时,时间开销就从循环变成固定开销,会快一点点。
-
自适应Level
很多实现都把level硬编码成全局或者实例级别的常量,比如在gostl中就是如此。 sl.maxLevel是一个实例级别的固定常量,跳表创建后便不再修改,因此有两个问题:
首先,当实际元素很少时,查找函数中循环的前几次cur变量基本上都是空指针,白白浪费时间查找,所以他的实现里 defaultMaxLevel设置的很小 。
其次,由于默认的maxLevel很小(只有10),插入1024个元素后,最上层基本上就接近平衡二叉树的情况了。如果再继续插入大量的元素,每层索引节点数量都快速增加,性能急剧下降。如果在构造时就根据预估容量设置一个足够大的maxLevel,可避免这个问题。但是很多时候这个数不是那么好预估,而且用起来不方便,漏设置又可能会导致意料之外的性能恶化。
因此我们把level设计为根据元素的个数动态自适应调整: 设置一个level成员记录最高的level值; 当插入元素时,如果出现了更高的层,再插入后就调大level; 当删除元素时,如果最顶层的索引变空了,就减少level。 通过这种方式,就解决了上述问题。
// Insert inserts a key-value pair into the skiplist.
// If the key is already in the skip list, it's value will be updated.
func (sl *SkipList[K, V]) Insert(key K, value V) {
// 处理key已存在的情况,略去
level := sl.randomLevel()
node = newSkipListNode(level, key, value)
// 插入链表,略去
if level > sl.level {
// Increase the level
for i := sl.level; i < level; i++ {
sl.head.next[i] = node
}
sl.level = level
}
sl.len++
}
为了防止在一开始元素个数很小时就生成了很大的随机level,我们在 randomLevel 里做了一下限制,最大允许生成的level为log2(Len())+2(2是个拍脑袋决定的余量)。
-
插入删除优化
插入时如果key不存在或者删除时节点存在,需要找到每层索引中的前一个节点,放入prevs数组返回,用于插入或者删除节点后各层链表的重新组织。 gostl的实现,是先在findPrevNodes函数里的循环中得到所有的prevs,然后再比较[0]层的值来判断key是否相等决定更新或者返回。源码如下:
https://github.com/liyue201/gostl/blob/e5590f19a43ac53f35893c7c679b37d967c4859c/ds/skiplist/skiplist.go#L186-L201
这个函数会从顶层遍历到最底层:
func (sl *Skiplist) findPrevNodes(key interface{}) []*Node {
prevs := sl.prevNodesCache
prev := &sl.head
for i := sl.maxLevel - 1; i >= 0; i-- {
if sl.head.next[i] != nil {
for next := prev.next[i]; next != nil; next = next.next[i] {
if sl.keyCmp(next.key, key) >= 0 {
break
}
prev = &next.Node
}
}
prevs[i] = prev
}
return prevs
}
插入时,再取最底层的节点的下一个,进一步比较是否相等:
// Insert inserts a key-value pair into the skiplist
func (sl *Skiplist) Insert(key, value interface{}) {
prevs := sl.findPrevNodes(key)
if prevs[0].next[0] != nil && sl.keyCmp(prevs[0].next[0].key, key) == 0 {
// 如果相等,其实prevs就没用了,但是findPrevNodes里依然进行了查询
// same key, update value
prevs[0].next[0].value = value
return
}
...
}
值得注意得失,再插入key时如果已经节点存在,或者删除key时节点不存在,是不需要调整每层节点的,前面辛辛苦苦查找的prevs就没用了。 我们在这里做了个优化,在这种情况下提前返回,不再继续找所有的prevs。 以插入为例:
// findInsertPoint returns (*node, nil) to the existed node if the key exists,
// or (nil, []*node) to the previous nodes if the key doesn't exist
func (sl *skipListOrdered[K, V]) findInsertPoint(key K) (*skipListNode[K, V], []*skipListNode[K, V]) {
prevs := sl.prevsCache[0:sl.level]
prev := &sl.head
for i := sl.level - 1; i >= 0; i-- {
for next := prev.next[i]; next != nil; next = next.next[i] {
if next.key == key {
// Key 已经存在,停止搜索
return next, nil
}
if next.key > key {
// All other node in this level must be greater than the key,
// search the next level.
break
}
prev = next
}
prevs[i] = prev
}
return nil, prevs
}
node和prevs只会有一个不空:
// Insert inserts a key-value pair into the skiplist.
// If the key is already in the skip list, it's value will be updated.
func (sl *SkipList[K, V]) Insert(key K, value V) {
node, prevs := sl.impl.findInsertPoint(key)
if node != nil {
// Already exist, update the value
node.value = value
return
}
// 生成及插入新节点,略去
}
删除操作的优化方式类似,不再赘述。
-
数据类型特有的优化
Ordered类型的跳表如果是升序的,可以直接用NewSkipList来创建。 对于用得较少的降序或者Key是不可比较的类型,就需要通过传入的比较函数来比较Key 。
一开始的实现为了简化。对于Ordered的SkipList,我们是通过调用SkipListFunc来实现的。这样可以节省不少代码,实现起来很简单。 但是Benchmark时,跑不过一些较快地实现。主要原因在 比较函数的函数调用 上。以查找为例:
// Get returns the value associated with the passed key if the key is in the skiplist, otherwise returns nil
func (sl *Skiplist) Get(key interface{}) interface{} {
var pre = &sl.head
for i := sl.maxLevel - 1; i >= 0; i-- {
cur := pre.next[i]
for ; cur != nil; cur = cur.next[i] {
cmpRet := sl.keyCmp(cur.key, key)
if cmpRet == 0 {
return cur.value
}
if cmpRet > 0 {
break
}
pre = &cur.Node
}
}
return nil
}
在C++中,比较函数可以是无状态的函数对象,其()运算符是可以inline的。但是在Go中, 比较函数只能是函数指针 ,sl.keyCmp调用无法被inline。因此简单的类型,其开销占的比例很大。
我们一开始用的优化手法,是在运行期间根据硬编码的key的类型,进行类型转换后调优化的实现。这种方式虽然凑效但是代码可读性差。其中,用到了硬编码的类型列表、运行期类型switch等机制,甚至还需要代码生成。
后来我们摸索出更优的方法。 通过同一个接口,基于比较Key是作为Ordered还是通过Func的方式,来提供不同实现的方式 。这不需要任何强制类型转换:
type skipListImpl[K any, V any] interface {
findNode(key K) *skipListNode[K, V]
lowerBound(key K) *skipListNode[K, V]
upperBound(key K) *skipListNode[K, V]
findInsertPoint(key K) (*skipListNode[K, V], []*skipListNode[K, V])
findRemovePoint(key K) (*skipListNode[K, V], []*skipListNode[K, V])
}
// NewSkipList creates a new SkipList for Ordered key type.
func NewSkipList[K Ordered, V any]() *SkipList[K, V] {
sl := skipListOrdered[K, V]{}
sl.init()
sl.impl = (skipListImpl[K, V])(&sl)
return &sl.SkipList
}
// NewSkipListFunc creates a new SkipList with specified compare function keyCmp.
func NewSkipListFunc[K any, V any](keyCmp CompareFn[K]) *SkipList[K, V] {
sl := skipListFunc[K, V]{}
sl.init()
sl.keyCmp = keyCmp
sl.impl = skipListImpl[K, V](&sl)
return &sl.SkipList
}
对于 Len()、IsEmpty()等,则不放进接口里。这有利于编译器inline优化。
2)内存分配优化
无论是理论上还是实测,内存分配对性能的影响还是较大。Go不像Java和C#的堆内存分配那么简单,因此 应当减少不必要的内存分配 。
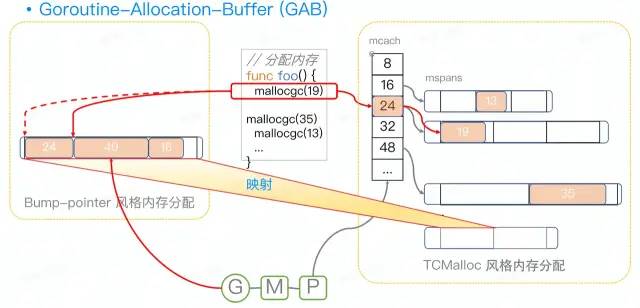
图来源:Go 生态下的字节跳动大规模微服务性能优化实践
-
Cache Prevs节点
在插入时,如果节点先前不存在或者删除时节点存在,那么就需要获得所有层的指向该位置的节点数组。全网有好几个实现案例都采用了在SkipList实例级别预先分配一个slice的办法,经测试比起每次都创建slice返回确实有相当明显的性能提升。
-
节点分配优化
不同level的节点数据类型是相同的,但是其next指针数组的长度不同。一些简单粗暴的实现是设置为固定的最大深度,由于跳表中绝大多数节点都只落在最低几层,浪费了较多的内存。
另外一种做法是改为动态分配,那么就多一次内存分配。 我们的做法是根据不同的深度定义不同的结构体,额外包含一个相应长度的nexts节点指针数组。在node的next切片指向这个数组,可以就减少一次内存分配。 并且由于nexts数组和node的地址是在一起的,cache局部性也更好。
// newSkipListNode creates a new node initialized with specified key, value and next slice.
func newSkipListNode[K any, V any](level int, key K, value V) *skipListNode[K, V] {
switch level {
case 1:
n := struct {
head skipListNode[K, V]
nexts [1]*skipListNode[K, V]
}{head: skipListNode[K, V]{key, value, nil}}
n.head.next = n.nexts[:]
return &n.head
case 2:
n := struct {
head skipListNode[K, V]
nexts [2]*skipListNode[K, V]
}{head: skipListNode[K, V]{key, value, nil}}
n.head.next = n.nexts[:]
return &n.head
// 一直到 case 40 ...
}
}
这么多啰嗦的代码
不适合手写,可以
弄个bash脚本通过go generate生成
。
我们在调试这段代码时发现,go的switch case语句对简单的全数值,也是通过二分法而非C++常用的跳转表来实现的。也许是因为有更耗时的内存分配,我们尝试把case 1、2等单独拿出来也没有提升。因此,暂且估计这里对性能没有影响。 如果case非常多的话,可以考虑对最常见的case单独处理,或者用函数指针数组来优化。

C++实现
类似的代码在C++中由于支持模板非类型参数,可以简单不少:
template <typename K, typename V>
struct Node {
K key;
V value;
size_t level;
Node* nexts[0];
SkipListNode(key, V value) : level(level), key(std::move(key)), value(std::move(value)) {}
};
template <typename K, typename V, int N> // 注意 N 可以作为模板参数
struct NodeN : public Node {
NodeN(K key, V value) : Node(N, key, value) {}
Node* nexts[N] = {};
};
Node* NewNode(int level, K key, V value) {
switch (level) {
case 1: return new NodeN<K, V, 1>(key, value);
case 2: return new NodeN<K, V, 2>(key, value);
case 3: return new NodeN<K, V, 3>(key, value);
...
}
}
用C(当然在C++中也可以用)的flexible array代码则会更简单一些:
Node* NewNode(int level, K key, V value) {
auto p = malloc(sizeof(Node*) + level * sizeof(Node*));
return new(p) Node(std::move(key), std::move(value));
}
由于C和C++中的next数组,不需要通过切片(相当于指针)来指向nexts数组,少了一次内存寻址,所以理论上性能更好一些。 C++实现为Go代码的手工转译,功能未做充分的验证,仅供对比评测。

Benchmark
sean-public@github.com实现了一个以float64为key的跳表,并和其他实现做了个比较,证明自己的最快。相关地址如下:
https://github.com/sean-public/fast-skiplist
https://github.com/sean-public/skiplist-survey
我们在他的基础上添加了一些其他的实现和我们的实现,做了benchmark。优化的数据类型优化就是基于此评测结果做的。相关地址如下:
https://github.com/chen3feng/skiplist-survey
以下是部分评测结果,数值越小越好:
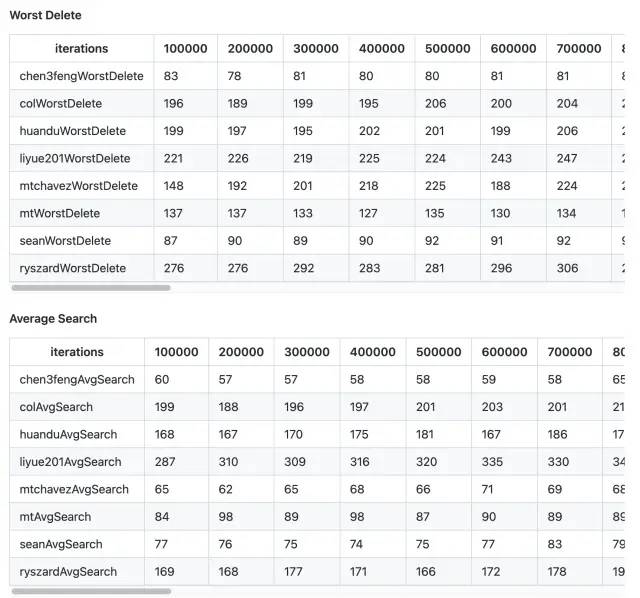
虽然有少量指标不是最快的,但是总体上(大部分指标)超越了我们在github上找到的其他实现。并且大部分其他实现key只支持int64或者float64,使得无法用于string等类型。
另外,我们也对C++的实现测了一下性能:
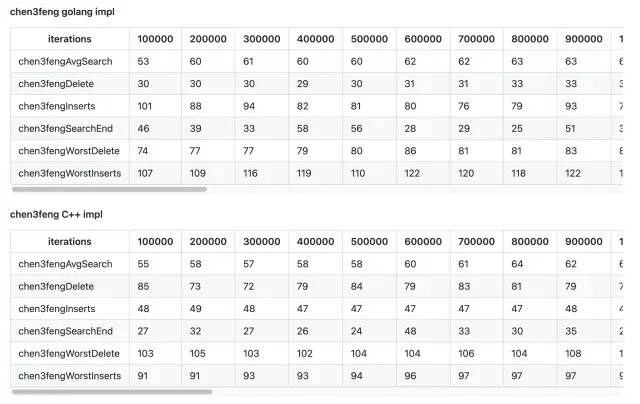
我们发现Go的实现性能很多指标基本接近C++,其中Delete反而更快一些。是因为C++在删除时要析构节点并释放内存,而Go采用GC的方式延后旁路处理。欢迎交流讨论。
源码:https://github.com/chen3feng/stl4go
推荐阅读
我为大家整理了一份 从入门到进阶的Go学习资料礼包 ,包含学习建议:入门看什么,进阶看什么。 关注公众号 「polarisxu」,回复 ebook 获取;还可以回复「进群」,和数万 Gopher 交流学习。
