今天介绍的第 007 号分析思维模型，可以很好地回答这个问题。

1. 模型介绍

在统计学里面，正态分布是一种很常见的模型，像人的寿命、血压、考试成绩、测量误差等等，都属于正态分布。

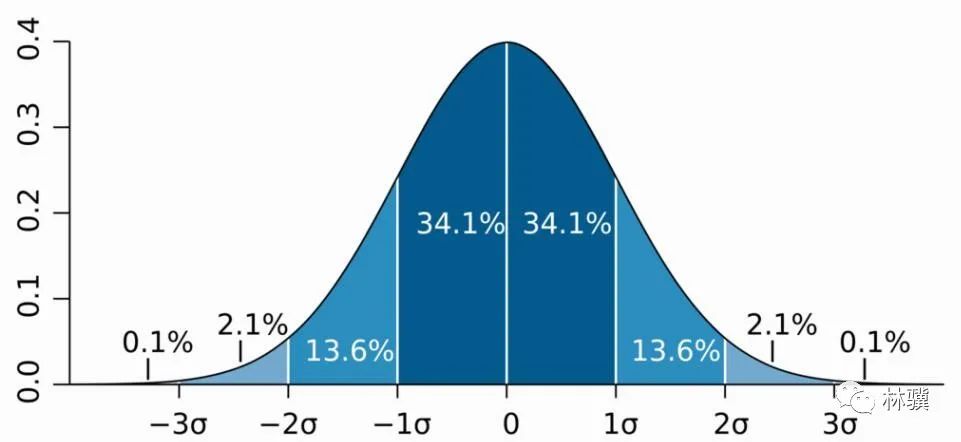
为什么正态分布模型很常见呢？

根据中心极限定理，如果一个事物受到多种相互独立的随机因素的影响，不管每个因素本身是什么分布，最终结果都属于正态分布。

许多事物都受到多种因素的影响，所以导致正态分布很常见。

正态分布的特点，是大部分数据都离平均值很近，几乎不可能出现极端异常的值。所以在现实世界中，你看不到一吨重的老鼠，也看不到一斤重的大象。

2. 应用举例

正态分布在生产管理中经典应用是「六西格玛」方法，简写为「6σ」，也就是对产品属性进行建模，明确误差要减小到什么程度，产品合格率才算达标。这样企业就有了量化的目标，从而可以花大力气去改善产品的质量。

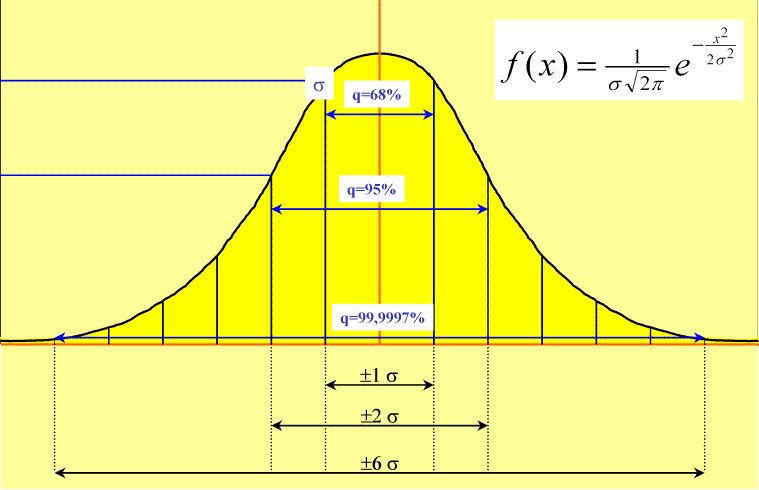
假设有一家专业制造汽车配件的公司，生产一种直径为 21 毫米的螺丝，误差不能超过 1 毫米，也就是说，螺丝直径范围必须在 20-22 毫米之间，否则有可能导致安全事故，因此必须做好产品质量管理。

由于螺丝直径的误差是很多种随机因素导致的，例如金属质量的变化、机器振动、温度和速度的波动等等，所以根据中心极限定理，推断螺丝的直径应该服从正态分布。

公司不可能精确地测量每一个螺丝的直径，通常会采取随机抽样的方法，根据样本来计算平均值和标准差，假设平均值是 21 毫米，6σ 等于 1，也就是说，基准标准差等于 1/6，如果能够达到这个标准，那么生产出来的产品质量就是比较可靠的，产品合格的概率高达 99.99968%，这并不容易，需要持续改进才有可能做到。

管理的实践，并不是计算出标准差就万事大吉，而是需要做很多非常艰巨的工作，来使得实际的标准差确实降到基准值以内。

我们学习分析思维模型，也不是理解了它的原理就好了，而是要把它应用到实践中，用它来解决现实中遇到的难题。

3. Python实践

我用 Python 模拟六个骰子，每个骰子的点数是随机的，从 1 到 6 的概率都是 1/6，如果把六个骰子的点数相加，然后画出分布图，与正态分布很接近。

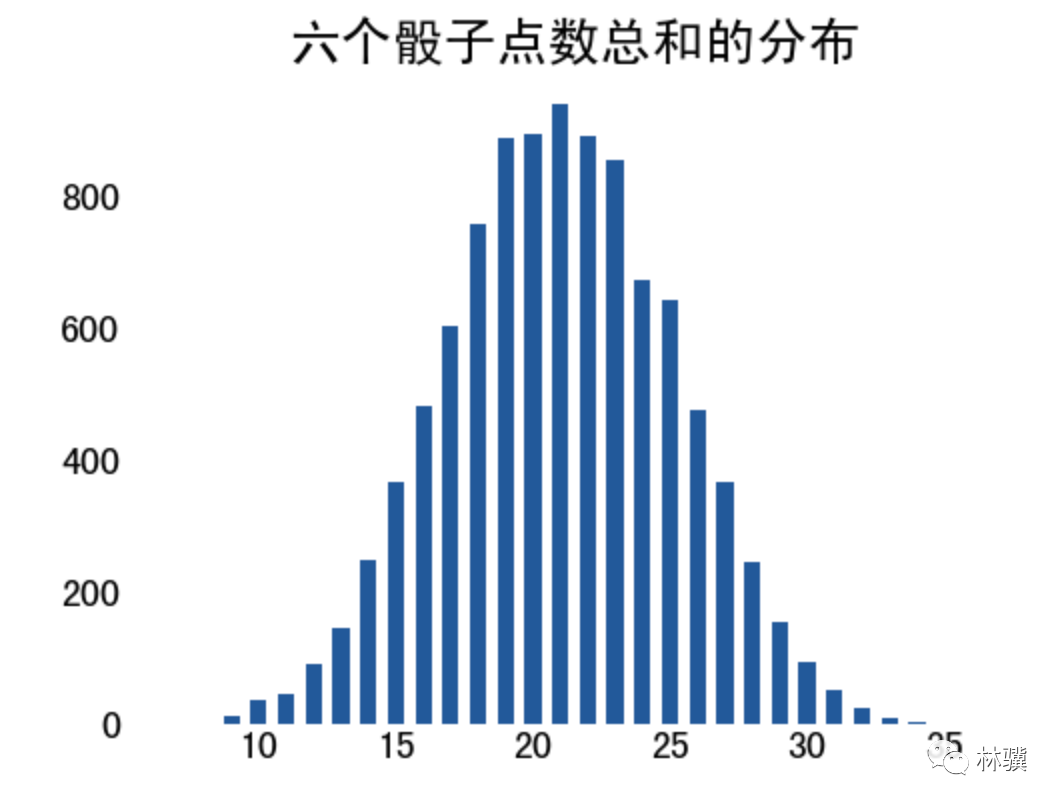
从这个例子也可以看出，中心极限定理在发挥作用，尽管每个骰子的点数都不属于正态分布，但是六个骰子相加起来的点数服从正态分布。

具体实现代码如下：

# 导入所需的库
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

# 正常显示中文标签
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 模拟骰子产生随机整数
np.random.seed(666666)
df = pd.DataFrame(np.random.randint(1, 7, (10000, 6)))

# 对骰子点数求和
df['总和'] = df.apply(lambda x: x.sum(), axis=1)

# 对点数之和进行计数
total = df.groupby(['总和'])['总和'].count()

# 画图用的数据定义
x = total.index
y = total.values

# 使用「面向对象」的方法画图
fig, ax = plt.subplots(figsize=(8, 6))

# 设置标题
ax.set_title("六个骰子点数总和的分布", fontsize=26, loc='center')

# 画柱形图
ax.bar(x, y, width=0.6, color='#00589F')

# 隐藏边框
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)

# 隐藏刻度线
ax.tick_params(axis='x', which='major', length=0)
ax.tick_params(axis='y', which='major', length=0)

# 设置坐标标签字体大小
ax.tick_params(labelsize=20)

plt.show()

小结

虽然世界是复杂多变的，但是多种独立因素综合起来的结果，又能用简单直观的正态分布模型来解释，这充分体现了数学之美。

用数学和图表来展现分析思维模型，能够帮助我们更好地理解世界运行的规律。

掌握多种分析思维模型，能够提高我们推理、解释、设计、沟通、行动、预测和探索的能力，从而实现对世界更加细致的理解。