不到30行代码实现一个酷炫H5全景
点击上方 前端瓶子君,关注公众号
回复算法,加入前端编程面试算法每日一题群
前言:本文将围绕:了解什么是全景 --> 怎么构成全景 --> 全景交互原理来进行讲解,手把手教你从零基础实现一个酷炫的Web全景,并讲解其中的原理。小白也能学习,建议收藏学习,有任何疑问,请在评论区讨论,笔者经常查看并回复。
一、了解什么是全景
1.1 全景定义
定义:全景是某一空间的_全部_景色。
通俗地说:大家都拍过照片,那我们想想一下拍照片的过程:站在某个空间,拿着相机,朝着某一角度拍摄,就可以获得这角度的景色照片了,而全景呢?是站在某个空间,拿着相机站着,朝着360角度拍摄,获得所有角度的景色照片,组合起来,再通过专门的技术展示给大家看的可交互的照片。
全景示例:

Jietu20210527-113413-HD.gif
体验二维码(支持微信扫码):
image.png
1.2 全景展示方式
全景的展示方式有很多中,比如:柱体全景、立方体全景、球体全景等等……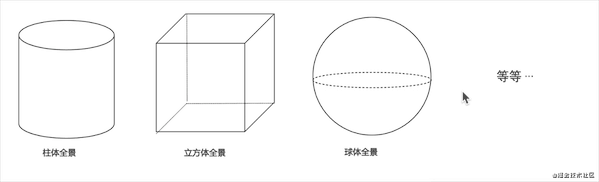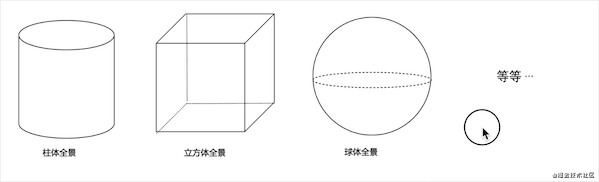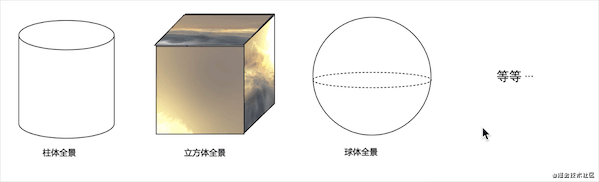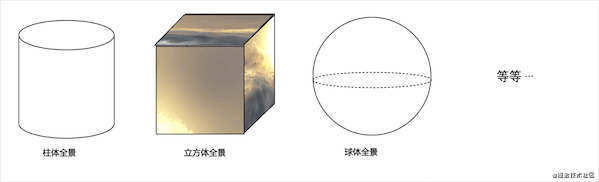
最最通俗的理解:用一个大的纸箱套在头上,看的场景(这种展示方式就是立方体全景)

image.png
柱体、立方体存在交叉区域,界面在交叉区域交互会呈现死角。所以,最好全景呈现方式是球体全景,360度无死角,本文将以球体全景来讲解。
二、怎么构成全景
2.1 认识ThreeJS
目前主流全景的前端实现方式:
| 实现方式 | 费用 | 是否开源 | 学习成本 | 开发难度 | 兼容性 | 扩展 | 性能 |
|---|---|---|---|---|---|---|---|
| CSSS 3D | 免费 | 是 | 中 | 难 | 支持CSS3D的浏览器 | 易 | 低 |
| ThreeJS | 免费 | 是 | 高 | 中 | 支持WebGL的部分浏览器 | 易 | 高 |
| 全景工具(Krpano) | 收费 | 否 | 易 | 无 | 支持flash和canvas的浏览器 | 难 | 中 |
作为一个有追求(瞎折腾)前端开发,当然要选择ThreeJS!!!
ThreeJS是Three(3D)+JS(JavaScript),它封装了底层的WebGL接口,使得我们能够在不了解图形学知识的前提下,也能用简单的代码实现三维场景的渲染。
要想在屏幕中展示3D图像,大致思路:
第一步:构建一个空间直角坐标系 :Three中称之为场景(Scene)
第二步:在坐标系中,绘制几何体:Three中的几何体有很多种,包括BoxGeometry(立方体),SphereGeometry(球体)等等
第三步:选择一个观察点,并确定观察方向等:Three中称之为相机(Camera)
第四步:将观察到的场景渲染到屏幕上的指定区域 :Three中使用Renderer完成这一工作(相当于拍照)
以上是ThreeJS渲染物体的固定写法,不理解的话记住也行的😄
球体全景所需的图片素材(下图):宽是高的两倍,数值是2的整数倍最好,建议图片宽高为2048px*1024px(后面实现全景会用到哈)

image.png
具体代码实现:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>手把手教你制作酷炫Web全景</title>
<meta name="viewport" id="viewport" content="width=device-width,initial-scale=1,minimum-scale=1, maximum-scale=1, user-scalable=no, viewport-fit=cover">
</head>
<body>
<div id="wrap" style="position: absolute;z-index: 0;top: 0;bottom: 0;left: 0;right: 0;width: 100%;height: 100%;overflow: hidden;">
</div>
<script src="https://cdn.bootcdn.net/ajax/libs/three.js/r128/three.js"></script>
<script>
const width = window.innerWidth
const height = window.innerHeight
const radius = 500 // 球体半径
// 第一步:创建场景
const scene = new THREE.Scene()
// 第二步:绘制一个球体
const geometry = new THREE.SphereBufferGeometry(radius, 32, 32)
const material = new THREE.MeshBasicMaterial({
map: new THREE.TextureLoader().load('./img/1.jpeg') // 上面的全景图片
})
const mesh = new THREE.Mesh(geometry, material)
scene.add(mesh)
// 第三步:创建相机,并确定相机位置
const camera = new THREE.PerspectiveCamera(75, width / height, 0.1, 100)
camera.position.x = 0 // 确定相机位置
camera.position.y = 0
camera.position.z = 100
camera.target = new THREE.Vector3(radius, 0, 0) // 设定对焦点
// 第四步:拍照并绘制到canvas
const renderer = new THREE.WebGLRenderer()
renderer.setSize(width, height) // 设置照片大小
document.querySelector('#wrap').appendChild(renderer.domElement) // 绘制到canvas
function render() {
camera.lookAt(camera.target) // 对焦
renderer.render(scene, camera) // 拍照
// 不断渲染,因为图片加载和处理需要时间,不确定何时拍照合适
requestAnimationFrame(render)
}
render()
</script>
</body>
</html>
复制代码
浏览器页面效果(记得开启手机模拟调试):

image.png
2.2 基础知识点
2.2.1 经纬度
本文是使用经纬度来操作全景,需要科普一下经纬度的知识
经纬度是经度与纬度的合称组成一个坐标系统。称为地理坐标系统,它是一种利用三度空间的球面来定义地球上的空间的球面坐标系统,能够标示地球表面上的任何一个位置。
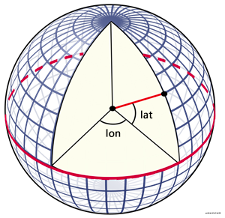
image.png
如图所示,经度:lon,取值范围:[0,360],纬度:lat,取值范围:[-90,90];
2.2.2 经纬度转换三维坐标
球面的点{lon,lat},其中R为球体的半径,求球面的点的在ThreeJS的坐标的位置为:
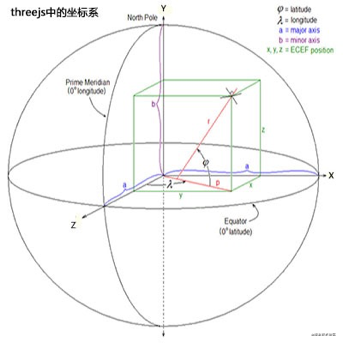
image.png
解:
X = R * cos(lat)* sin( lon )
Y = R * sin( lat )
Z = R * cos( lat )*cos( lon )
注:ThreeJS中默认的坐标系是右手坐标系,X轴为左右,Y轴为上下,Z轴为前后。
2.3 生成全景的步骤
在2.1的章节中,我们已经完成了绘制一个球体,绘制全景是在其基础上要做调整:
1、将相机移到球体的球心位置;
2、将全景图片贴到球体的内表面;
具体步骤如下:
第一步:创建一个场景(Scene)
第二步:创建一个球体,并将全景图片贴到球体的内表面,放入场景中
第四步:创建一个透视投影相机将camera拉到球体的中心,相机观看球体内表面
第五步:通过修改经纬度来,改变相机观察的点
具体代码实现:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>手把手教你制作酷炫Web全景</title>
<meta name="viewport" id="viewport" content="width=device-width,initial-scale=1,minimum-scale=1, maximum-scale=1, user-scalable=no, viewport-fit=cover">
</head>
<body>
<div id="wrap" style="position: absolute;z-index: 0;top: 0;bottom: 0;left: 0;right: 0;width: 100%;height: 100%;overflow: hidden;">
</div>
<script src="https://cdn.bootcdn.net/ajax/libs/three.js/r128/three.js"></script>
<script>
const width = window.innerWidth, height = window.innerHeight // 屏幕宽高
const radius = 50 // 球体半径
// 第一步:创建场景
const scene = new THREE.Scene()
// 第二步:绘制一个球体
const geometry = new THREE.SphereBufferGeometry(radius, 32, 32)
geometry.scale(-1, 1, 1) // 球面反转,由外表面改成内表面贴图
const material = new THREE.MeshBasicMaterial({
map: new THREE.TextureLoader().load('./img/1.jpeg') // 上面的全景图片
})
const mesh = new THREE.Mesh(geometry, material)
scene.add(mesh)
// 第三步:创建相机,并确定相机位置
const camera = new THREE.PerspectiveCamera(75, width / height, 0.1, 100)
camera.position.x = 0 // 确定相机位置移到球心
camera.position.y = 0
camera.position.z = 0
camera.target = new THREE.Vector3(radius, 0, 0) // 设置一个对焦点
// 第四步:拍照并绘制到canvas
const renderer = new THREE.WebGLRenderer()
renderer.setPixelRatio(window.devicePixelRatio)
renderer.setSize(width, height) // 设置照片大小
document.querySelector('#wrap').appendChild(renderer.domElement) // 绘制到canvas
renderer.render(scene, camera)
let lat = 0, lon = 0
function render() {
lon += 0.003 // 每帧加一个偏移量
// 改变相机的对焦点,计算公式参考:2.2.2章节
camera.target.x = radius * Math.cos(lat) * Math.cos(lon);
camera.target.y = radius * Math.sin(lat);
camera.target.z = radius * Math.cos(lat) * Math.sin(lon)
camera.lookAt(camera.target) // 对焦
renderer.render(scene, camera)
requestAnimationFrame(render)
}
render()
</script>
</body>
</html>
复制代码
效果:

Jietu20210527-172203-HD.gif
至此,我们全景制作已经完成了,(只统计js代码:共_28行_代码,我才不是标题党呢?😁)。
三、全景交互原理
3.1 手势交互之旋转
手势交互之旋转指单指滑动操作,这与滑动地球仪的交互是一致的。
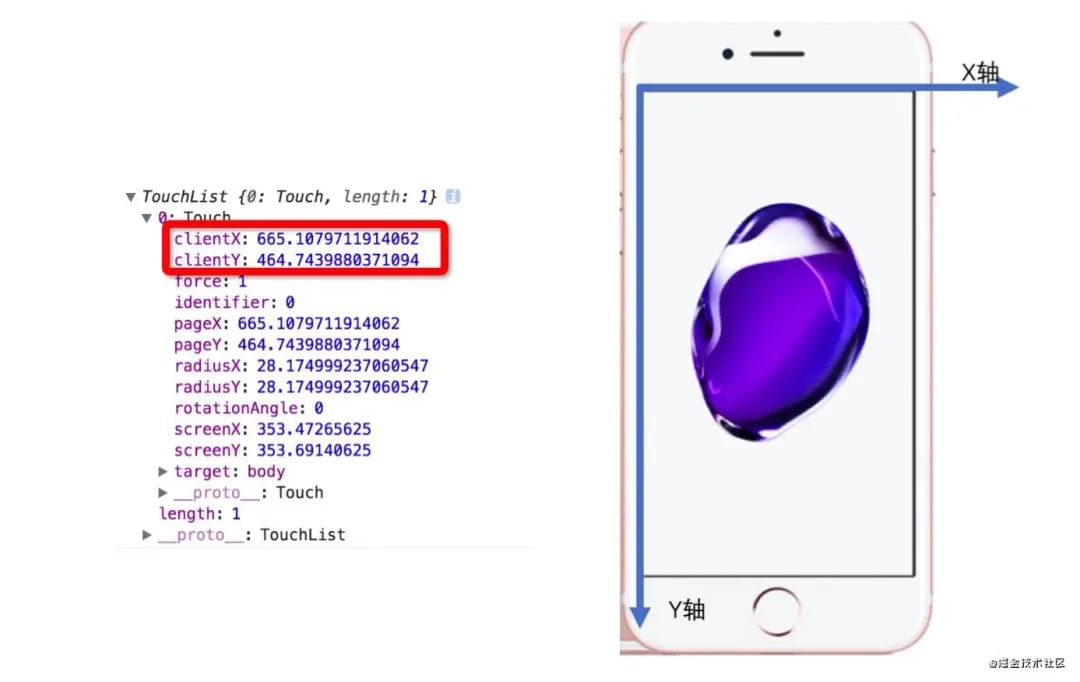
屏幕坐标系,左上角为原点,X轴:由左向右,Y轴:由上到下, 手指在屏幕滑动会依次触发三个事件:touchstart、touchmove和touchend;event对象中记录了手指屏幕的位置
TeamTalk_IMG_2021-05-27-173217.jpg
手指在屏幕滑动过程:
touchstart:记录滑动起始的位置(startX,startY)
touchmove:记录当前位置(curX,curY)相减上一次位置的值,计算出弧长除于半径乘以factor,计算出(lon,lat)
touchend:暂时没有用的
其中:弧长R值的是屏幕的滑动距离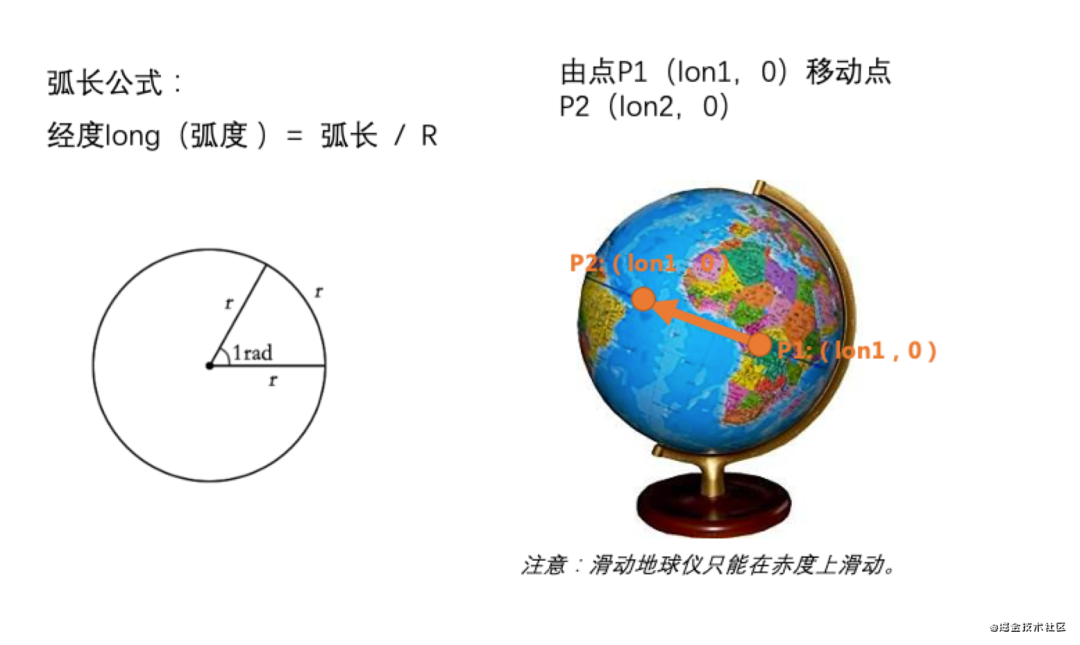
那么单指在屏幕的滑动,由P1 (clientX1,clientY1)移动到P2 (clientX1,clientY1)长度为,对应经纬度变化:
distanceX = clientX1 - clientX2 // X轴方向
distanceY = clientY1 - clientY2 // Y轴方向
// 其中R为球体半径,根据弧长公式:
lon = distanX / R
lat = distanY / R
复制代码
代码实现:
// 增加touch事件监听
let lastX, lastY // 上次屏幕位置
let curX, curY // 当前屏幕位置
const factor = 1 / 10 // 灵敏系数
const $wrap = document.querySelector('#wrap')
// 触摸开始
$wrap.addEventListener('touchstart', function (evt) {
const obj = evt.targetTouches[0] // 选择第一个触摸点
startX = lastX = obj.clientX
startY = lastY = obj.clientY
})
// 触摸中
$wrap.addEventListener('touchmove', function (evt) {
evt.preventDefault()
const obj = evt.targetTouches[0]
curX = obj.clientX
curY = obj.clientY
// 参考:弧长公式
lon -= ((curX - lastX) / radius) * factor // factor为了全景旋转平稳,乘以一个灵敏系数
lat += ((curY - lastY) / radius) * factor
lastX = curX
lastY = curY
})
复制代码
单指操作效果:

上面的代码已经加上全景的单指交互,但是,缺少了旋转惯性。接下来,我们加一下惯性动画:
滑动惯性实现,手指在屏幕滑动过程:
touchstart:记录滑动起始的位置(startX,startY, startTime)
touchmove:记录当前位置(curX,curY)相减上一次位置的值,乘以factor,计算出(lon,lat),【触摸跟随】
touchend:记录endTime,计算本次滑动过程中的平均速度,然后,每帧减去减速度d,直至速度为0或者touchstart事件被触发 【触摸结束触发惯性动画】
代码实现:
let lastX, lastY // 上次屏幕位置
let curX, curY // 当前屏幕位置
let startX, startY // 开始触摸的位置,用于计算速度
let isMoving = false // 是否停止单指操作
let speedX, speedY // 速度
const factor = 1 / 10 // 灵敏系数,经验值
const deceleration = 0.1 // 减速度,惯性动画使用
const $wrap = document.querySelector('#wrap')
// 触摸开始
$wrap.addEventListener('touchstart', function (evt) {
const obj = evt.targetTouches[0] // 选择第一个触摸点
startX = lastX = obj.clientX
startY = lastY = obj.clientY
startTime = Date.now()
isMoving = true
})
// 触摸中
$wrap.addEventListener('touchmove', function (evt) {
evt.preventDefault()
const obj = evt.targetTouches[0]
curX = obj.clientX
curY = obj.clientY
// 参考:弧长公式
lon -= ((curX - lastX) / radius) * factor // factor为了全景旋转平稳,乘以一个系数
lat += ((curY - lastY) / radius) * factor
lastX = curX
lastY = curY
})
// 触摸结束
$wrap.addEventListener('touchend', function (evt) {
isMoving = false
var t = Date.now() - startTime
speedX = (curX - startX) / t // X轴方向的平均速度
speedY = (curY - startY) / t // Y轴方向的平均速度
subSpeedAnimate() // 惯性动画
})
let animateInt
// 减速度动画
function subSpeedAnimate() {
lon -= speedX * factor // X轴
lat += speedY * factor
// 减速度
speedX = subSpeed(speedX)
speedY = subSpeed(speedY)
// 速度为0或者有新的触摸事件,停止动画
if ((speedX === 0 && speedY === 0) || isMoving) {
if (animateInt) {
cancelAnimationFrame(animateInt)
animateInt = undefined
}
} else {
requestAnimationFrame(subSpeedAnimate)
}
}
// 减速度
function subSpeed(speed) {
if (speed !== 0) {
if (speed > 0) {
speed -= deceleration;
speed < 0 && (speed = 0);
} else {
speed += deceleration;
speed > 0 && (speed = 0);
}
}
return speed;
}
复制代码
预览地址:azuoge.github.io/Opanorama/
3.2 手势交互之缩放
手势交互之缩放是双指操作,跟放大图片一样。
前面介绍ThreeJS,提到过相机,全景缩放也是依据相机拍照时,缩放拍摄照片内容的原理是一样的。
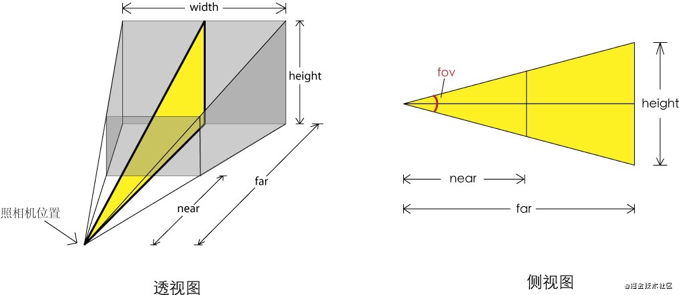
image.png
使用ThreeJS创建相机代码如下:
const camera = new THREE.PerspectiveCamera( fov , aspect , near , fear )
复制代码
参数说明:

image.png
其中,
near:取默认值:0.1即可
fear:只要大于球体半径就可,取值为:球体半径R
aspect:在全景的场景已经确定了,照片的长宽比:屏幕宽度 / 屏幕高度
fov:视场,缩放是通过修改它的值来完成全景图片的缩放;
其实,很好理解,睁大眼睛,我们就看的视野就广,看到物体就显得小些【缩小】,反之,眯着眼,看到的视野就窄,看到物体就显得大【放大】,可以通过修改右图的 fov 的值来缩放全景图片
那么如何计算fov呢?这时候我们需要双指交互,同计算,开始触摸计算第一次双指的距离,在双指移动中不断计算双指距离,与上一次距离相除即为缩放倍数。
关键代码如下:
// 其中,(clientX1,clientY1)和(clientX2,clientY2)为双指在屏幕的当前位置
// 计算距离,简化运输不用平方计算
const distance = Math.abs(clientX1 - clientX2) + Math.abc(clientY1 - clientY)
// 计算缩放比
const scale = distance / lastDiance
// 计算新的视角
fov = camera.fov / scale
// 视角范围取值
camera.fov = Math.min(90, Math.max(fov,60)) // 90 > fov > 60 ,从参数说明中选取
// 视角需要主动更新
camera.updateProjectionMatrix()
复制代码
体验地址:azuoge.github.io/Opanorama/
3.3 手机陀螺仪交互
html5事件中,deviceorientation事件,此事件是检测设备方向变化时的事件。
H5有两份坐标:
地球坐标 x/y/z:在任何情况下,都是恒定方向
手机平面坐标 x/y/z:相对于手机屏幕定义的方向
取值范围:
X轴:上下旋转Beta(X) ,取值范围:[ -180° ~ 180° ]
Z轴:左右旋转扭曲Alpha(Z) ,取值范围:[ 0°, 360° ]
Y轴:扭转可以是 Gamma(Y) ,取值范围:[ -90° ,90° ]
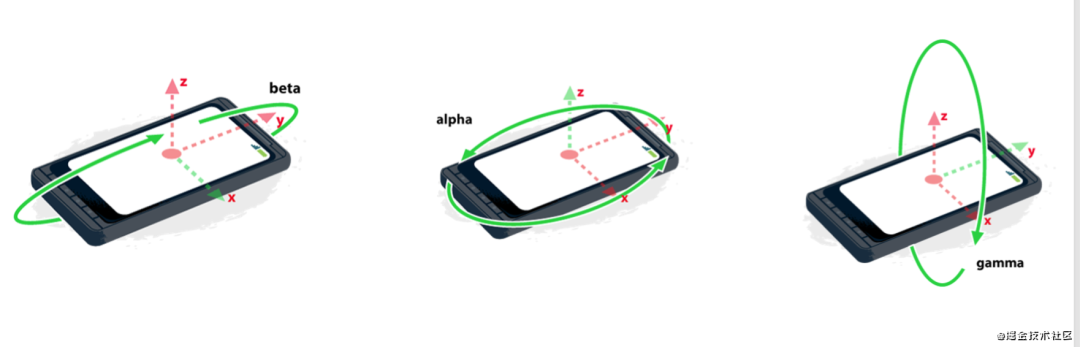
image.png
当将手机垂直,且正面(90度)冲着自己。
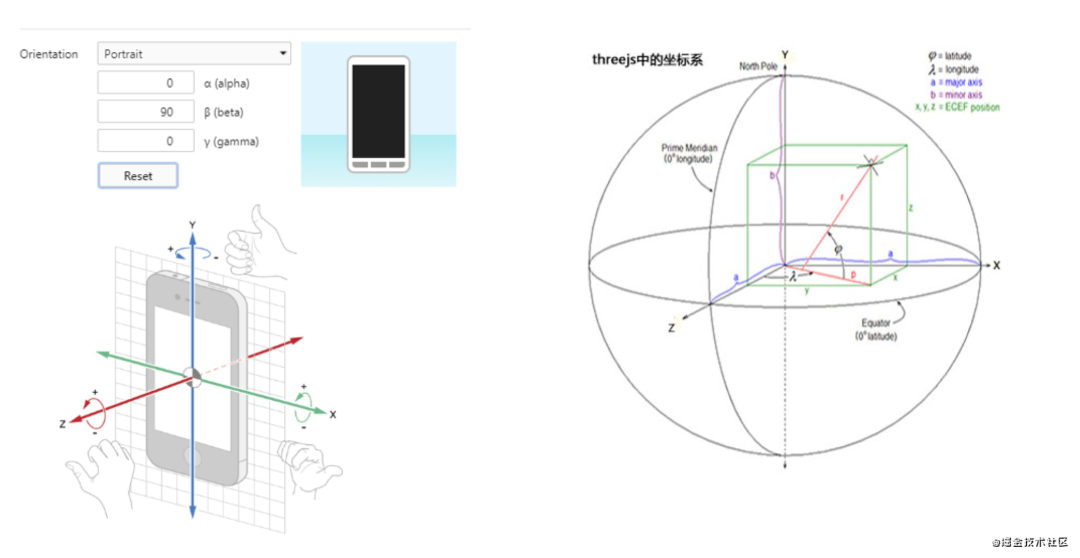
image.png
从上图观察,并结合ThreeJS的坐标系,可以得出关键结论:
lat对应 (beta - 90) * (Math.PI / 180) 【角度换算弧度】
lon对应 gamma * (Math.PI / 180) 【角度换算弧度】
这alpha角度就不再这次全景交互中。
当将将手机垂直,且正面(90度)冲着自己,转动手机方向演示
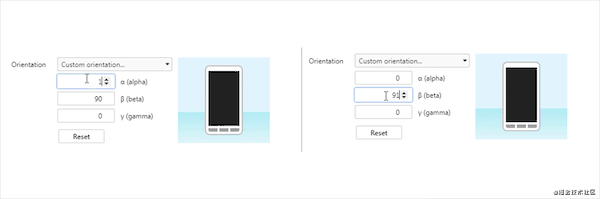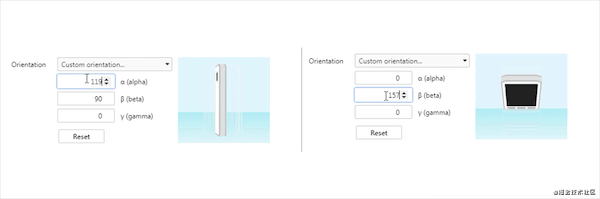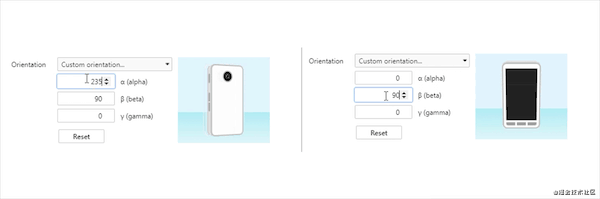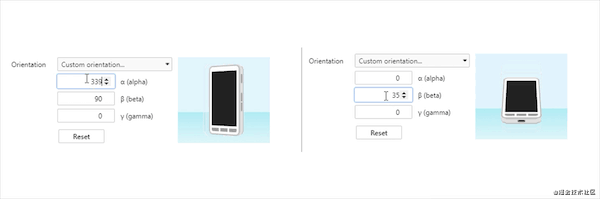
Jietu20210530-104349-HD.gif
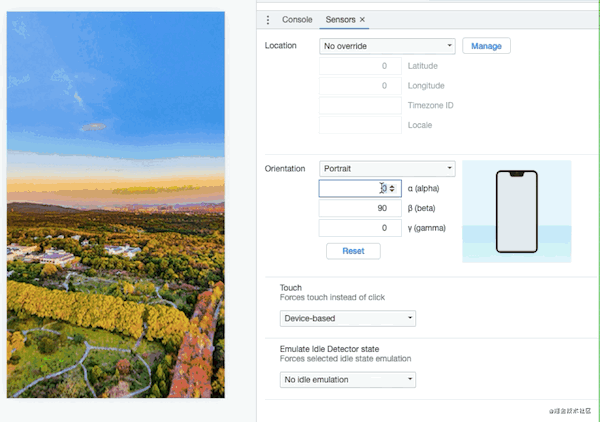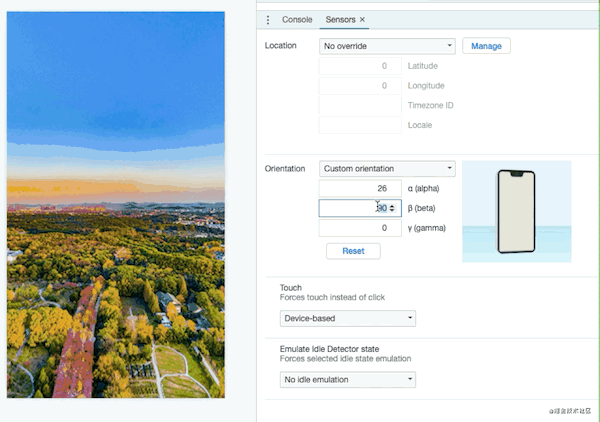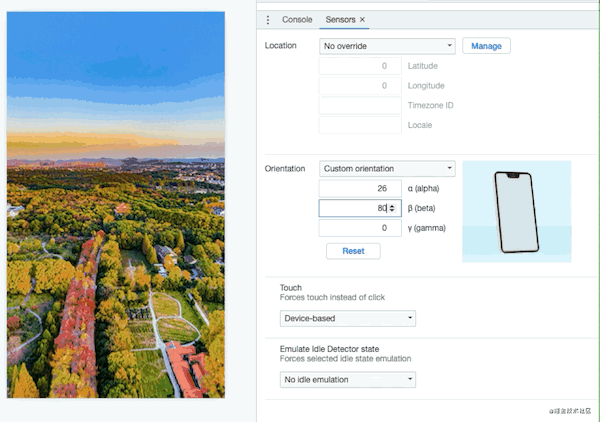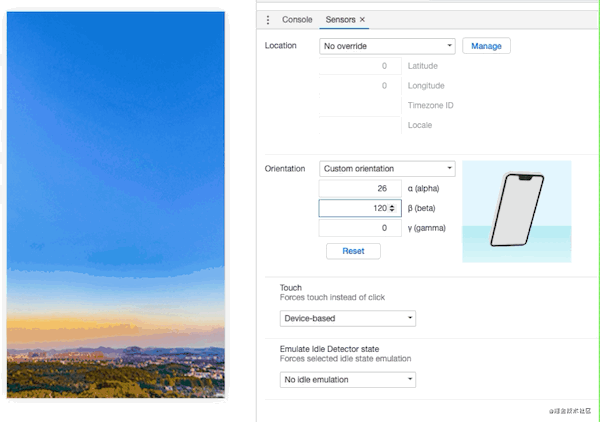
Chrome浏览器是可以开启陀螺仪模拟,操作如下:
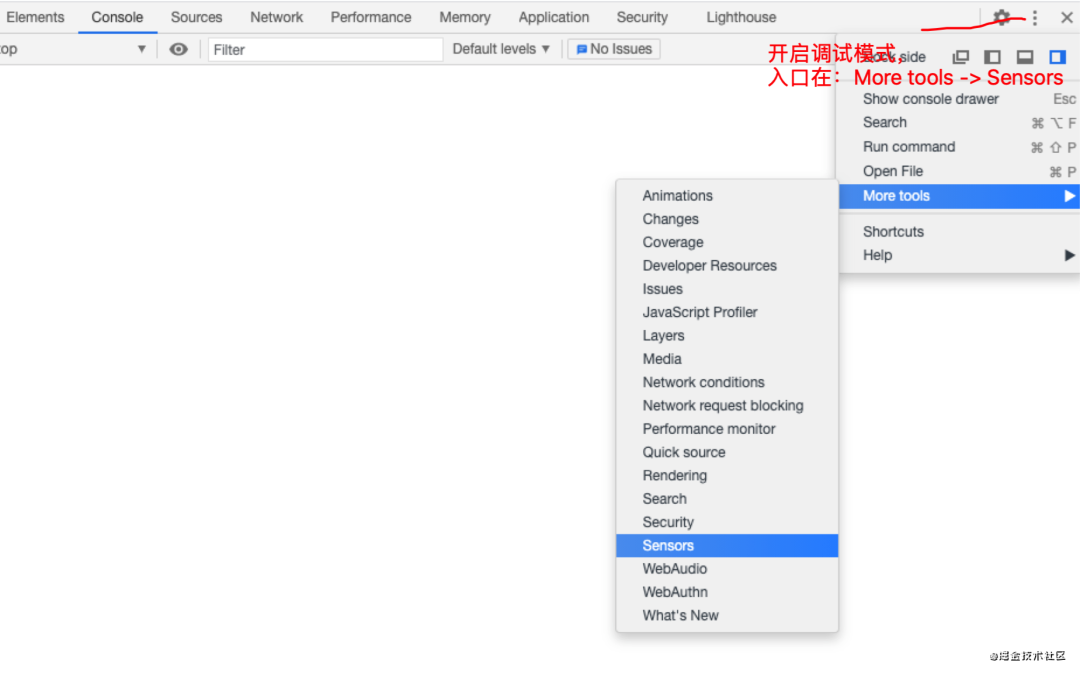
image.png
那么代码就很简单:
// 角度换算弧度公式
const L = Math.PI / 180
// 陀螺仪交互
window.addEventListener('deviceorientation', function (evt) {
lon = evt.alpha * L
lat = (evt.beta - 90) * L
})
复制代码
效果如下:
Jietu20210530-112850-HD.gif
需要注意的是:H5获取的手机方向数值,在部分android手机,存在明显的抖动,就算手机静止放在桌面上,陀螺仪输出的数据也会抖动;(该问题不属于原理,只是在全景应用过程遇到的问题,不感兴趣的同学可以跳过😄)

Jietu20210530-112405-HD.gif
我们需要对陀螺仪的输出的数字做处理,这里采用信号传输中使用的 低通滤波算法
公式如下:
 当K=1时,就是真实的数据,小于1,就可以稀释变化值。
当K=1时,就是真实的数据,小于1,就可以稀释变化值。
但是又有了新的问题:灵敏度和平稳度的矛盾
滤波系数越小,滤波结果越平稳,但是灵敏度越低
滤波系数越大,灵敏度越高,但是滤波结果越不稳定
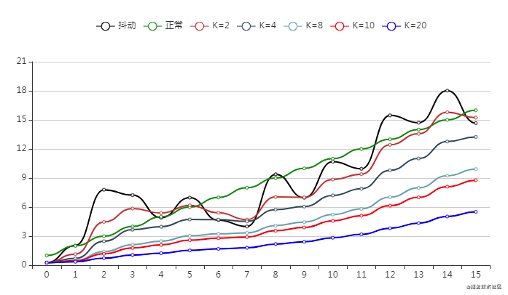
image.png
通过统计数据得出的结论, K取值为10,灵敏度和平稳度表现较好。
体验地址:azuoge.github.io/Opanorama/
3.4 手势和陀螺仪交互结合
手势和陀螺仪的交互都转化成经纬度来驱动全景,那么,两者结合也就很简单了。
具体思路如下:
lat = touch.lat + orienter.lat + fix.lat // 取值范围:[-90,90]
lon = touch.lon + orienter.lon + fix.lon // 取值范围:[0,360]
复制代码
其中,touch为手势影响,orienrer为陀螺仪影响,fix为修正因子,保证经纬度在换算的结果始终符合取值范围。
本文完整的代码放在: https://github.com/azuoge/Opanorama,欢迎查阅和讨论。
关于本文
来源:azuo
https://juejin.cn/post/6968263858309824526
最后
欢迎关注【前端瓶子君】✿✿ヽ(°▽°)ノ✿
回复「算法」,加入前端编程源码算法群,每日一道面试题(工作日),第二天瓶子君都会很认真的解答哟!
回复「交流」,吹吹水、聊聊技术、吐吐槽!
回复「阅读」,每日刷刷高质量好文!
如果这篇文章对你有帮助,「在看」是最大的支持
》》面试官也在看的算法资料《《
“在看和转发”就是最大的支持
