来源：集智俱乐部

本文约23000字，建议阅读20+分钟 
本文整理自丁鹏老师的8篇短文，从多角度回顾了因果推断的各种模型方法。

[ 导读 ] 推断因果关系，是人类思想史与科学史上的重要主题。现代因果推断的研究，始于约尔-辛普森悖论，经由鲁宾因果模型、随机试验等改进，到朱力亚·珀尔的因果革命，如今因果科学与人工智能的结合正掀起热潮。

1. 因果推断简介之一：从 Yule-Simpson’s Paradox 讲起

2. 因果推断简介之二：Rubin Causal Model (RCM) 和随机化试验

3. 因果推断简介之三：R. A. Fisher 和 J. Neyman 的分歧

4. 因果推断简介之四：观察性研究，可忽略性和倾向得分

5. 因果推断简介之五：因果图 (Causal Diagram)

6. 因果推断简介之六：工具变量（instrumental variable）

7. 因果推断简介之七：Lord’s Paradox

8. 因果推断简介之八：吸烟是否导致肺癌？Fisher versus Cornfield

1. 因果推断简介之一：
从 Yule-Simpson’s Paradox 讲起

在国内的时候，向别人介绍自己是研究因果推断（causal inference）的，多半的反应是：什么？统计还能研究因果？这确实是一个问题：统计研究因果，能、还是不能？直接给出回答，比较冒险；如果有可能，我需要花一些篇幅来阐述这个问题。

目前市面上能够买到的相关教科书仅有 2011 年图灵奖得主 Judea Pearl 的 Causality: Models, Reasoning, and Inference。Harvard 的统计学家 Donald Rubin 和计量经济学家 Guido Imbens 合著的教科书历时多年仍尚未完成；Harvard 的流行病学家 James Robins 和他的同事也在写一本因果推断的教科书，本书目前只完成了第一部分，还未出版。我本人学习因果推断是从 Judea Pearl 的教科书入手的，不过这本书晦涩难懂，实在不适合作为入门的教科书。Donald Rubin 对 Judea Pearl 提出的因果图模型（causal diagram）非常反对，他的教科书中杜绝使用因果图模型。我本人虽然脑中习惯用图模型进行思考，但是还是更偏好 Donald Rubin 的风格，因为这对于入门者，可能更容易。不过这一节，先从一个例子出发，不引进新的统计符号和概念。

天才的高斯在研究天文学时，首次引进了最大似然和最小二乘的思想，并且导出了正态分布（或称高斯分布）。其中最大似然有些争议，比如 Arthur Dempster 教授说，其实高斯那里的似然，有贝叶斯或者信仰推断（fiducial inference）的成分。高斯那里的 “统计” 是关于 “误差” 的理论，因为他研究的对象是 “物理模型” 加“随机误差”。大约在 100 多年前，Francis Galton 研究了父母身高和子女身高的 “关系”，提出了“（向均值）回归” 的概念。众所周知，他用的是线性回归模型。此时的模型不再是严格意义的“物理模型”，而是“统计模型” — 用于刻画变量之间的关系，而不一定是物理机制。之后，Karl Pearson 提出了“相关系数”（correlation coefficient）。

后世研究的统计，大多是关于 “相关关系” 的理论。但是关于 “因果关系” 的统计理论，非常稀少。据 Judea Pearl 说，Karl Pearson 明确的反对用统计研究因果关系；有意思的是，后来因果推断为数不多的重要文章（如 Rosenbaum and Rubin 1983; Pearl 1995）都发表在由 Karl Pearson 创刊的 Biometrika 上。下面讲到的悖论，可以说是困扰统计的根本问题，我学习因果推断便是由此入门的。

在高维列联表分析中，有一个很有名的例子，叫做 Yule-Simpson’s Paradox。有文献称，Karl Pearson 很早就发现了这个悖论 ——也许这正是他反对统计因果推断的原因。此悖论表明，存在如下的可能性：X和Y在边缘上正相关；但是给定另外一个变量Z后，在Z的每一个水平上，X和Y都负相关。Table 1 是一个数值的例子，取自Pearl(2000)。

Table 1 中，第一个表是整个人群的数据：接受处理和对照的人都是 40 人，处理有较高的存活率，因此处理对整个人群有 “正作用”。第二个表和第三个表是将整个人群用性别分层得到的，因为第一个表的四个格子数，分别是下面两个表对应格子数的和：

奇怪的是，处理对男性有 “负作用”，对女性也有 “负作用”。一个处理对男性和女性都有 “负作用”，但是他对整个人群却有 “正作用”：悖论产生了！

有人可能会认为这种现象是由于随机性或者小样本的误差导致的。但是这个现象与样本量无关，与统计的误差也无关。比如，将上面的每个格子数乘以一个巨大的正数，上面的悖论依然存在。

纯数学的角度，上面的悖论可以写成初等数学

；这并无新奇之处。但是在统计上，这具有重要的意义——变量之间的相关关系可以完全的被第三个变量 “扭曲”。更严重的问题是，我们的收集的数据可能存在局限性，忽略潜在的“第三个变量” 可能改变已有的结论，而我们常常却一无所知。鉴于 Yule-Simpson 悖论的潜在可能，不少人认为，统计不可能用来研究因果关系。

上面的例子是人工构造的，在现实中，也存在不少的实例正是 Yule-Simpson’s Paradox。比如，UC Berkeley 的著名统计学家 Peter Bickel 教授 1975 年在 Science 上发表文章，报告了 Berkeley 研究生院男女录取率的差异。他发现，总体上，男性的录取率高于女性，然而按照专业分层后，女性的录取率却高于男性 (Bickel 等 1975)。

在流行病学的教科书 (如 Rothman 等 2008) 中，都会讲到 “混杂偏倚”（confounding bias），其实就是 Yule-Simpson’s Paradox，书中列举了很多流行病学的实际例子。

由于有 Yule-Simpson’s Paradox 的存在，观察性研究中很难得到有关因果的结论，除非加上很强的假定，这在后面会谈到。比如，一个很经典的问题：吸烟是否导致肺癌？由于我们不可能对人群是否吸烟做随机化试验，我们得到的数据都是观察性的数据：即吸烟和肺癌之间的相关性（正如 Table 1 的合并表）。此时，即使我们得到了吸烟与肺癌正相关，也不能断言 “吸烟导致肺癌”。这是因为可能存在一些未观测的因素，他既影响个体是否吸烟，同时影响个体是否得癌症。比如，某些基因可能使得人更容易吸烟，同时容易得肺癌；存在这样基因的人不吸烟，也同样得肺癌。此时，吸烟和肺癌之间相关，却没有因果作用。

相反的，我们知道放射性物质对人体的健康有很大的伤害，但是铀矿的工人平均寿命却不比常人短；这是流行病学中有名的 “健康工人效应”（healthy worker effect）。这样一来，似乎是说铀矿工作对健康没有影响。但是，事实上，铀矿的工人通常都是身强力壮的人，不在铀矿工作寿命会更长。此时，在铀矿工作与否与寿命不相关，但是放射性物质对人的健康是有因果作用的。

这里举了一个悖论，但没有深入的阐释原因。阐释清楚这个问题的根本原因，其实就讲清楚了什么是因果推断。这在后面会讲到。作为结束，留下如下思考的问题：

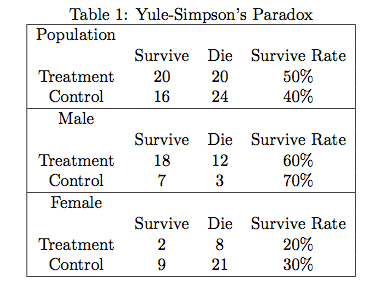
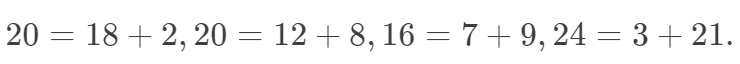
Table 1 中，处理组和对照组中，男性的比例分别为多少？这对悖论的产生有什么样的影响？反过来考虑处理的 “分配机制”（assignment mechanism），计算P(Treatment∣Male)和 P(Treatment∣Female)。
假如(X，Y，Z)服从三元正态分布，X和Y正相关，Y和Z正相关，那么X和Z是否正相关？（北京大学概率统计系 09 年《应用多元统计分析》期末第一题）
流行病学的教科书常常会讲各种悖论，比如混杂偏倚（confounding bias）和入院率偏倚（Berkson’s bias）等，本质上是否与因果推断有关？
计量经济学中的 “内生性”（endogeneity）怎么定义？它和 Yule-Simpson 悖论有什么联系？

2. 因果推断简介之二：
Rubin Causal Model (RCM) 和随机化试验

因果推断用的最多的模型是 Rubin Causal Model (RCM; Rubin 1978) 和 Causal Diagram (Pearl 1995)。Pearl (2000) 中介绍了这两个模型的等价性，但是就应用来看，RCM 更加精确，而 Causal Diagram 更加直观，后者深受计算机专家们的推崇。这部分主要讲 RCM。

设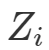表示个体 i接受处理与否，处理取1，对照取0 (这部分的处理变量都讨论二值的，多值的可以做相应的推广)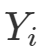；表示个体 i的结果变量。另外记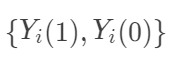表示个体 i接受处理或者对照的潜在结果 (potential outcome)，那么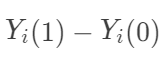表示个体 i 接受治疗的个体因果作用。不幸的是，每个个体要么接受处理，要么接受对照，中必然缺失一半，个体的因果作用是不可识别的。观测的结果是。但是，在Z做随机化的前提下，我们可以识别总体的平均因果作用 (Average Causal Effect; ACE）：

这是因为

最后一个等式表明

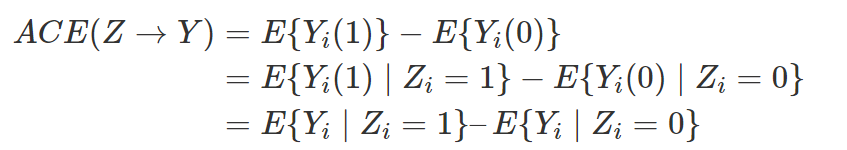
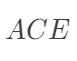可以由观测的数据估计出来。其中第一个等式用到了期望算子的线性性（非线性的算子导出的因果度量很难被识别！)；第二个式子用到了随机化，即

其中，

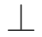表示独立性。由此可见，随机化试验对于平均因果作用的识别起着至关重要的作用。

当Y是二值的时候，平均因果作用是流行病学中常用的“风险差”（risk difference; RD）：

当然，流行病学还常用“风险比”（risk ratio; RR）：

和“优势比”（odds ratio; OR）：

上面的记号都带着“C”，是为了强调“causal”。细心的读者会发现，定义 CRR 和 COR 的出发点和 ACE 不太一样。ACE 是通过对个体因果作用求期望得到的，但是 CRR 和 COR 是直接在总体上定义的。这点微妙的区别还引起了不少人的研究兴趣。比如，经济学中的某些问题，受到经济理论的启示，处理的作用可能是非常数的，仅仅研究平均因果作用不能满足实际问题的需要。这时候，计量经济学家提出了“分位数处理作用”（quantile treatment effect: QTE）：

在随机化下，这个量也是可以识别的。但是，其实这个量并不能回答处理作用异质性（heterogenous treatment effects）的问题，因为处理作用非常数，最好用如下的量刻画：

这个量刻画的是处理作用的分布。不幸的是，估计

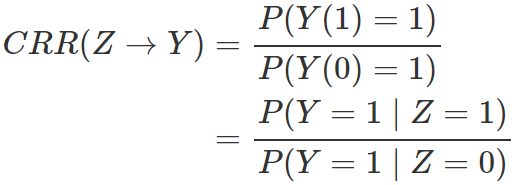
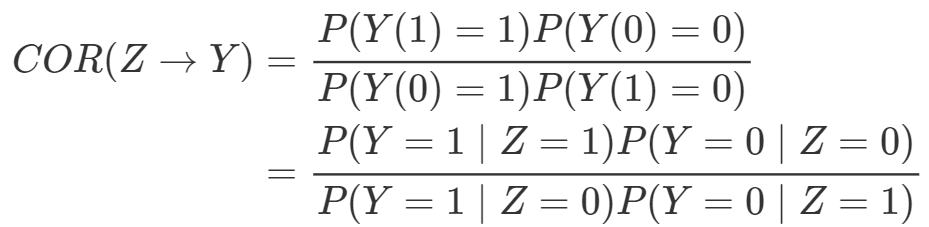
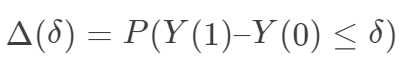
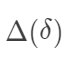需要非常强的假定，通常不具有可行性。

作为结束，留下如下的问题：

“可识别性”（identifiability）在统计中是怎么定义的？
医学研究者通常认为，随机对照试验（randomized controlled experiment）是研究处理有效性的黄金标准，原因是什么呢？随机化试验为什么能够消除 Yule-Simpson 悖论？
在随机化下是可识别的。另外一个和它“对偶”的量是 Ju and Geng (2010) 提出的分布因果作用（distributional causal effect: DCE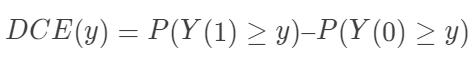）：，在随机化下也可以识别。
即使完全随机化，也不可识别。也就是说，经济学家提出的具有“经济学意义”的量，很难用观测数据来估计。这种现象在实际中常常发生：关心实际问题的人向统计学家索取的太多，而他们提供的数据又很有限。

关于 RCM 的版权，需要做一些说明。目前可以看到的文献，最早的是 Jerzy Neyman 于 1923 年用波兰语写的博士论文，第一个在试验设计中提出了“潜在结果”（potential outcome）的概念。后来 Donald Rubin 在观察性研究中重新（独立地）提出了这个概念，并进行了广泛的研究。Donald Rubin 早期的文章并没有引用 Jerzy Neyman 的文章，Jerzy Neyman 的文章也不为人所知。一直到 1990 年，D. M. Dabrowska 和 T. P. Speed 将 Jerzy Neyman 的文章翻译成英文发表在 Statistical Science 上，大家才知道 Jerzy Neyman 早期的重要贡献。今天的文献中，有人称 Neyman-Rubin Model，其实就是潜在结果模型。计量经济学家，如 James Heckman 称，经济学中的 Roy Model 是潜在结果模型的更早提出者。在 Donald Rubin 2004 年的 Fisher Lecture 中，他非常不满地批评计量经济学家，因为 Roy 最早的论文中，全文没有一个数学符号，确实没有明确的提出这个模型。详情请见，Donald Rubin 的 Fisher Lecture，发表在 2005 年的 Journal of the American Statistical Association 上。研究 Causal Diagram 的学者，大多比较认可 Donald Rubin 的贡献。但是 Donald Rubin 却是 Causal Diagram 的坚定反对者，他认为 Causal Diagram 具有误导性，且没有他的模型清楚。他与James Heckman （诺贝尔经济学奖）， Judea Pearl （图灵奖）和 James Robins 之间的激烈争论，成为了广为流传的趣闻。

3. 因果推断简介之三：
R. A. Fisher 和 J. Neyman 的分歧

R.A.Fisher

这部分谈到的问题非常微妙：完全随机化试验下的 Fisher randomization test 和 Neyman repeated sampling procedure。简单地说，前者是随机化检验，或者如很多教科书讲的Fisher 精确检验（Fisher exact test）；后者是 Neyman 提出的置信区间（confidence interval）理论。

我初学因果推断的时候，并没有细致的追求这些微妙的区别，觉得了解到简介之二的层次就够了。不过在 Guido Imbens 和 Donald Rubin 所写的因果推断教科书（还未出版）中，这两点内容放在了全书的开端，作为因果推断的引子。在其他的教科书中，是看不到这样的讲法的。平日里常常听到 Donald Rubin 老爷子对 Fisher randomization test 的推崇，我渐渐地也被他洗脑了。

Fisher 的随机化检验，针对的是如下的零假设，又被称为 sharp null：

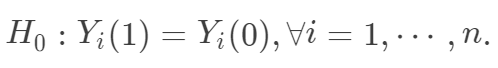坦白地说，这个零假设是我见过的最奇怪的零假设，没有之一。现行的统计教科书中，讲到假设检验，零假设都是针对某些参数的，而 Fisher 的 sharp null 看起来却像是针对随机变量的。这里需要讲明白的是，当我们关心有限样本（finite sample）的因果作用时，每个个体的潜在结果

都是固定的，观测变量

的随机性仅仅由于“随机化” 本身导致的。

理解清楚这点，才能理解 Fisher randomization test 和后面的 Neyman repeated sampling procedure。如果读者对于这种有限样本的思考方式不习惯，可以先阅读一下经典的抽样调查教科书，那里几乎全是有限样本的理论，所有的随机性都来自于随机采样的过程。

如果认为潜在结果是固定的数，那么 Fisher sharp null 就和现行的假设检验理论不相悖。这个 null 之所以“sharp”的原因是，在这个零假设下，所有个体的潜在结果都固定了，个体的因果作用为零，唯一的随机性来自于随机化的“物理”特性。定义处理分配机制的向量为

结果向量为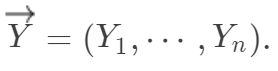

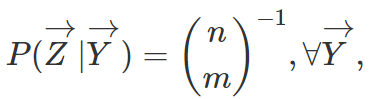
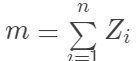此时有限样本下的随机化分配机制如下定义：

其中，

为处理组中的总数。这里的“条件期望”并不是说

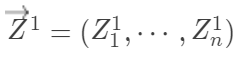是随机变量，而是强调处理的分配机制不依赖于潜在结果。比如，我们选择统计量

来检验零假设，问题在于这个统计量的分布不易求出。但是，我们又知道，这个统计量的分布完全来自随机化。因此，我们可以用如下的“随机化”方法（Monte Carlo 方法模拟统计量的分布）：将处理分配机制的向量进行随机置换得到

，计算此时的检验统计量

；如此重复多次n不大时，可以穷尽所有的置换，便可以模拟出统计量在零假设下的分布，计算出 p 值。

有人说，Fisher randomization test 已经蕴含了 bootstrap 的思想，似乎也有一定的道理。不过，这里随机化的方法是针对一个特例提出来的。

J. Neyman

下面要介绍的 Neyman 的方法，其实早于 Fisher 的方法。这种方法在 Neyman 1923 年的博士论文中，正式提出了。这种方法假定n个个体中有m个随机的接受处理，目的是估计（有限）总体的平均因果作用：

一个显然的无偏估计量是

但是，通常的方差估计量，

高估了方差，构造出来的置信区间在 Neyman – Pearson 意义下太“保守”。可以证明，在个体处理作用是常数的假定下，上面的方差估计是无偏的。

通常的教科书讲假设检验，都是从正态均值的检验开始。Neyman 的方法给出了的点估计和区间估计，也可以用来检验如下的零假设：

实际中，到底是 Fisher 和零假设合理还是 Neyman 的零假设合理，取决于具体的问题。比如，我们想研究某项政策对于中国三十多个省的影响，这是一个有限样本的问题，因为我们很难想象中国的省是来自某个“超总体”。但是社会科学中的很多问题，我们不光需要回答处理或者政策对于观测到的有限样本的作用，我们更关心这种处理或者政策对于一个更大总体的影响。前者，Fisher 的零假设更合适，后者 Neyman 的零假设更合适。

关于这两种角度的争论，可以上述到 Fisher 和 Neyman 两人。1935 年，Neyman 向英国皇家统计学会提交了一篇论文“Statistical problems in agricultural experimentation”，Fisher 和 Neyman 在讨论文章时发生了激烈的争执。不过，从今天的统计教育来看，Neyman 似乎占了上风。

用下面的问题结束：

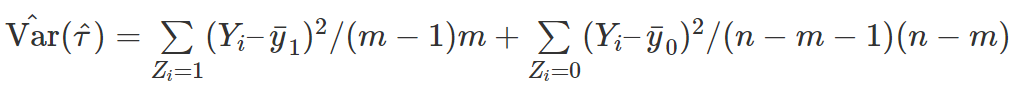
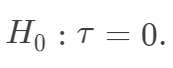
在 sharp null下，Neyman 方法下构造的 T 统计量，是否和 Fisher randomization test 构造的统计量相同？分布是否相同？
Fisher randomization test 中的统计量可以有其他选择，比如 Wilcoxon 秩和统计量等，推断的方法类似。
当Y是二值变量时，上面 Fisher 的方法就是教科书中的 Fisher exact test。在没有学习 potential outcome 这套语言之前，理解 Fisher exact test 是有些困难的。
证明。
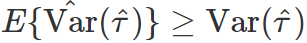假定n个个体是一个超总体（super-population）的随机样本，超总体的平均因果作用定义为那么 Neyman 的方法得到估计量是超总体平均因果作用的无偏估计，且方差的表达式是精确的；而 sharp null 在超总体的情形下不太适合。

4. 因果推断简介之四：

观察性研究，可忽略性和倾向得分

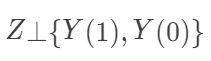这节采用和前面相同的记号。Z表示处理变量（1是处理，0是对照），Y表示结果，X表示处理前的协变量。在完全随机化试验中，可忽略性

成立，这保证了平均因果作用

可以表示成观测数据的函数，因此可以识别。在某些试验中，我们“先验的”知道某些变量与结果强相关，因此要在试验中控制他们，以减少试验的方差。在一般的有区组（blocking）的随机化试验中，更一般的可忽略性

成立，因为只有在给定协变量X后，处理的分配机制才是完全随机化的。比如，男性和女性中，接受处理的比例不同，但是这个比例是事先给定的。

在传统的农业和工业试验中，由于随机化，可忽略性一般是能够得到保证的；因此在这些领域谈论因果推断是没有太大问题的。Jerzy Neyman 最早的博士论文，就研究的是农业试验。但是，这篇写于 1923 年的重要统计学文章，迟迟没有得到统计学界的重视，也没有人将相关方法用到社会科学的研究中。1970 年代，Donald Rubin 访问 UC Berkeley 统计系，已退休的 Jerzy Neyman 曾问起：为什么没有人将潜在结果的记号用到试验设计之外？正如 Jerzy Neyman 本人所说 “without randomization an experiment has little value irrespective of the subsequent treatment（没有随机化的试验价值很小）”，人们对于观察性研究中的因果推断总是抱着强烈的怀疑态度。我们经常听到这样的声音：统计就不是用来研究因果关系的！

在第一讲 Yule-Simpson 悖论的评论中，有人提到了哲学（史）上的休谟问题（我的转述）：人类是否能从有限的经验中得到因果律？这的确是一个问题，这个问题最后促使德国哲学家康德为调和英国经验派（休谟）和大陆理性派（莱布尼兹-沃尔夫）而写了巨著《纯粹理性批判》。其实，如果一个人是绝对的怀疑论者（如休谟），他可能怀疑一切，甚至包括因果律，所以，康德的理论也不能完全“解决”休谟问题。怀疑论者是无法反驳的，他们的问题也是无法回答的。他们存在的价值是为现行一切理论起到警示作用。一般来说，统计学家不会从过度哲学的角度谈论问题。从前面的说明中可以看出，统计中所谓的“因果”是“某种”意义的“因果”，即统计学只讨论“原因的结果”，而不讨论“结果的原因”。前者是可以用数据证明或者证伪的；后者是属于科学研究所探索的。用科学哲学家卡尔·波普的话来说，科学知识的积累是“猜想与反驳”的过程：“猜想”结果的原因，再“证伪”原因的结果；如此循环即科学。

下面谈到的是，在什么样的条件下，观察性研究也可以推断因果。这是一切社会科学所关心的问题。答案是：可忽略性，即

。在可忽略性下，ACE可以识别，因为

从上面的公式来看，似乎我们的任务是估计两个条件矩E{Y|X, Z=z}(z=0,1). 这就是一个回归问题。不错，这也是为什么通常的回归模型被赋予“因果”含义的原因。如果我们假定可忽略性和线性模型

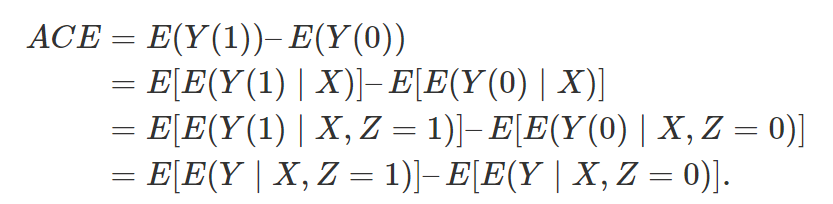
成立，那么

就表示平均因果作用。线性模型比较容易实现，实际中人们比较倾向这种方法。但是他的问题是：（1）假定个体因果作用是常数；（2）对于处理和对照组之间的不平衡（unbalance）没有很好的检测，常常在对观测数据外推（extrapolation）。

上面的第二条，是线性回归最主要的缺陷。在 Donald Rubin 早期因果推断的文献中，推崇的方法是“匹配”（matching）。一般来说，我们有一些个体接受处理，另外更多的个体接受对照；简单的想法就是从对照组中找到和处理组中比较“接近”的个体进行匹配，这样得出的作用，可以近似平均因果作用。“接近”的标准是基于观测协变量的，比如，如果某项研究，性别是唯一重要的混杂因素，我们就将处理组中的男性和对照组中的男性进行匹配。但是，如果观测协变量的维数较高，匹配就很难实现了。现有的渐近理论表明，匹配方法的收敛速度随着协变量维数的增高而线性的衰减。

后来 Paul Rosenbaum 到 Harvard 统计系读 Ph.D.，在 Donald Rubin 的课上问到了这个问题。这就促使两人合作写了一篇非常有名的文章，于 1983 年发表在 Biometrika 上：“The central role of the propensity score in observational studies for causal effects”。倾向得分定义为

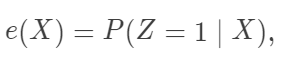容易验证，在可忽略性下，它满足性质

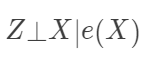（在数据降维的文献中，称之为“充分降维”，sufficient dimension reduction）和

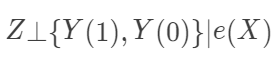（给定倾向得分下的可忽略性）。根据前面的推导，显然有 ACE=E[E(Y|e(X), Z=1)]-E[E(Y|e(X),Z=0)] 。此时，倾向得分是一维的，我们可以根据它分层（Rosenbaum 和 Rubin 建议分成 5 层），得到平均因果作用的估计。连续版本的分层，就是下面的加权估计：

不过，不管是分层还是加权，第一步我们都需要对倾向得分进行估计，通常的建议是 Logistic 回归。甚至有文献证明的下面的“离奇”结论：使用估计的倾向得分得到平均因果作用的估计量的渐近方差比使用真实的倾向得分得到的小。

熟悉传统回归分析的人会感到奇怪，直接将 Y对 Z和 X做回归的方法简单直接，为何要推荐倾向得分的方法呢？确实，读过 Rosenbaum 和 Rubin 原始论文的人，一般会觉得，这篇文章很有意思，但是又觉得线性回归（或者 logistic 回归）足矣，何必这么复杂？在因果推断中，我们应该更加关心处理机制，也就是倾向得分。按照 Don Rubin 的说法，我们应该根据倾向得分来“设计”观察性研究；按照倾向得分将人群进行匹配，形成一个近似的“随机化试验”。而这个设计的过程，不能依赖于结果变量；甚至在设计的阶段，我们要假装没有观察到结果变量。否则，将会出现如下的怪现象：社会科学的研究者不断地尝试加入或者剔除某些回归变量，直到回归的结果符合自己的“故事”为止。这种现象在社会科学中实在太普遍了！结果的回归模型固然重要，但是如果在 Y模型上做文章，很多具有“欺骗性”的有偏结果就会出现在文献中。这导致大多数的研究中，因果性并不可靠。

讲到这里，我们有必要回到最开始的 Yule-Simpson’s Paradox。用Z表示处理（1表示处理，0表示对照），Y表示存活与否（1是表示存活，0表示死亡），X表示性别（1表示男性，0表示女性）。目前我们有处理“因果作用”的两个估计量：一个不用性别进行加权调整

另一个用性别进行加权调整（由于此时协变量是一维的，倾向得分和协变量本身存在一一对应，用倾向得分调整结果相同，见下面问题 1）

其中，表示相应的矩估计。是否根据性别进行调整，对结果有本质的影响。当

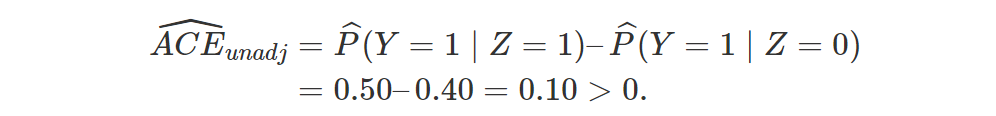
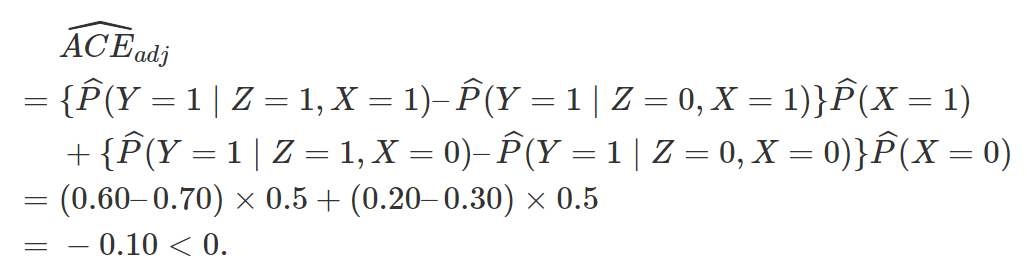
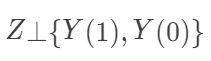时，第一个估计量是因果作用的相合估计；当

时，第二个估计量是因果作用的相合估计。根据实际问题的背景，我们应该选择哪个估计量呢？到此为止，回答这个问题有些似是而非（选择调整的估计量？），更进一步的回答，请听下回分解：因果图（causal diagram）。

作为结束，留下如下的问题：

如果X是二值的变量（如性别），那么匹配或者倾向的分都导致如下的估计量:
这个公式在流行病学中非常基本，即根据混杂变量进行分层调整。在后面的介绍中将讲到，这个公式被 Judea Pearl 称为“后门准则”（backdoor criterion）。
倾向得分的加权形式，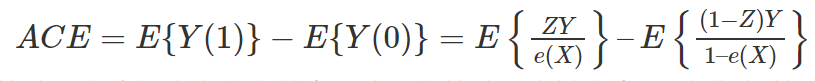
本质上是抽样调查中的 Horvitz-Thompson 估计。在流行病学的文献中，这样的估计量常被称为“逆概加权估计量”（inverse probability weighting estimator; IPWE）。
直观上，为什么估计的倾向得分会更好？想想偏差和方差的权衡（bias-variance tradeoff）。

关于“可忽略性”（ignorability），需要做一些说明。在中文翻译的计量经济学教科书中，这个术语翻译存在错误，比如 Wooldridge 的 Econometric Analysis of Cross Section and Panel Data 的中译本中，“可忽略性”被翻译成“不可知”。子曰：“名不正，则言不顺；言不顺，则事不成。”在 Rubin (1978) 中，“可忽略性”这个概念是在贝叶斯推断的框架下提出来的：当处理的分配机制满足这样的条件时，在后验的推断中，可将分配机制“忽略”掉。在传统的贝叶斯看来，所有的推断都是条件在观测数据上的，那么为什么处理的分配机制会影响贝叶斯后验推断呢？Donald Rubin 说，当时连 Leonard Jimmie Savage 和 Dennis Victor Lindley 都在此困惑不解，他 1978 年的文章，原意就是为了解释为什么随机化会影响贝叶斯推断。

“可忽略性” 这个名字最早是在缺失数据的文献中提出来的。当缺失机制是随机缺失（missing at random：MAR）且模型的参数与缺失机制的参数不同时，缺失机制“可忽略”（ignorable）。“可忽略”是指，缺失机制不进入基于观测数据的似然或者贝叶斯后验分布。

5. 因果推断简介之五：
因果图 (Causal Diagram)

这部分介绍 Judea Pearl 于 1995 年发表在 Biometrika 上的工作 “Causal diagrams for empirical research”，这篇文章是 Biometrika 创刊一百多年来少有的讨论文章，Sir David Cox，Guido Imbens, Donald Rubin 和 James Robins 等人都对文章作了讨论。由于 Judea Pearl 最近刚获得了图灵奖，我想他的工作会引起更多的关注（事实上计算机界早就已经过度的关注了）。

一、有向无环图和 do 算子

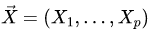为了避免过多图论的术语，这里仅仅需要知道有向图中“父亲”和“后代”的概念：有向箭头上游的变量是“父亲”，下游的变量是“后代”。在一个有向无环图（Directed Acyclic Graph；DAG）中，记所有的节点集合为

。这里用

表示连续变量的密度函数和离散变量的概率函数。有两种观点看待一个 DAG：一是将其看成表示条件独立性的模型；二是将其看成一个数据生成机制。当然，本质上这两种观点是一样的。在第一种观点下，给定 DAG 中某个节点的“父亲”节点，它与其所有的非“后代”都独立。根据全概公式和条件独立性，DAG 中变量的联合分布可以有如下的递归分解：

其中

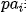表示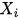

的“父亲”集合，即所有指向

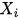的节点集合。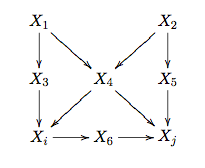

Figure 1: An Example of Causal Diagram

例子：在 Figure 1 中，联合分布可以分解成为

如果将 DAG 看成一个数据生成机制，那么它和下面的非参数结构方程模型是等价的：

注意，这个联立方程组是“三角的”（triangular）或者“递归的”（recursive），因为 DAG 中没有环，方程组中也就没有反馈。计量经济学中的联立方程组模型（simultaneous equation model: SEM），并不在这个讨论的框架下。DAG 用于描述数据的生成机制，而不常用于描述系统均衡时的状态；后者主要是 SEM 的目的。这样描述变量联合分布或者数据生成机制的模型，被称为“图模型”或者“贝叶斯网络”（Bayesian network）。

显然，一个有向无环图唯一地决定了一个联合分布；反过来，一个联合分布不能唯一地决定有向无环图。反过来的结论不成立，对我们的实践有很重要的意义，比如 Figure 2 中的两个有向无环图，原因和结果不同，图的结构也不同；但是，我们观测到的联合分布

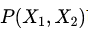可以有两种分解

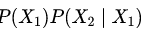和

因此，我们从观测变量的联合分布，很难确定“原因”和“结果”。在下一节图模型结构的学习中，我们会看到，只有在一些假定和特殊情形下，我们可以从观测数据确定“原因”和“结果”。

用一个 DAG 连表示变量之间的关系，并不是最近才有的。图模型也并不是 Judea Pearl 发明的。但是，早期将图模型作为因果推断的工具，成果并不深刻，大家也不太清楚仅仅凭一个图，怎么能讲清楚因果关系。教育、心理和社会学中常用的结构方程模型（structural equation model: SEM），就是早期的尝试；甚至可以说 SEM 是因果图的先驱。（注意，这里出现的两个 SEM 表示不同的模型！）

DAG 中的箭头，似乎表示了某种“因果关系”。但是，要在 DAG 上引入“因果”的概念，则需要引进 do 算子，do 的意思可以理解成“干预” （intervention）。没有“干预”的概念，很多时候没有办法谈因果关系。在 DAG 中

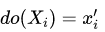（也可以记做

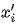），表示如下的操作：将

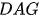中指向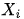

的有向边全部切断，且将

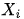的取值固定为常数

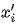. 如此操作，得到的新

的联合分布可以记做

可以证明，干预后的联合分布为

请注意，

在绝大多数情况下是不同的。

例子：考虑如下的两个 DAG：

在 Figure 2 (1) 中，有。由于

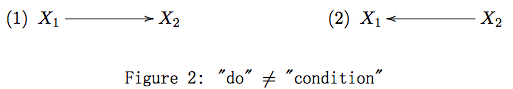
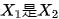的“原因”，“条件”和“干预

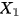，对应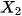

的分布相同。但是在 Figure 2 (2) 中，有. 由于

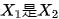的“结果”，“条件”（或者“给定”）“结果”，“原因”的分布不再等于他的边缘分布，但是人为的“干预”“结果

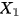，并不影响“原因

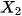的分布。

根据 do 算子，便可以定义因果作用。比如二值的变量

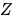对于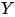

的平均因果作用定义为

上面 do 算子下的期望，分别对应 do 算子下的分布。这样在 do 算子下定义的因果模型，被已故计量经济学家 Halbert White 称为 Pearl Causal Model (PCM; White and Chalak 2009)。Pearl 在其书中写到：

“I must take the opportunity to acknowledge four colleagues who saw clarity shining through the do(x) operator before it gained popularity: Steffen Lauritzen, David Freedman, James Robins and Philip David. Phil showed special courage in pringting my paper in Biometrika, the journal founded by causality’s worst adversary – Karl Pearson.” (Pearl, 2000)

在书中 Pearl 论述了 RCM 和 PCM 的等价性，即

其中

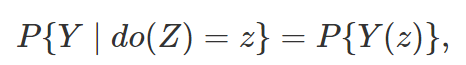
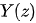表示潜在结果。要想说明两个模型的等价性，可以将潜在结果嵌套在 DAG 所对应的数据生成机制之中，所有的潜在结果

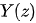都由这个非参数结构方程模型产生：

其中，

表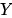

除的父亲节点。上面的方程表示：

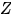的值强制z时，DAG 系统所产生

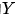值。这个意义下，do 算子导出的结果，就是“潜在结果”。

二、 d分离，前门准则和后门准则

在上面的叙述中，如果整个 DAG 的结构已知且所有的变量都可观测，那么我们可以根据上面 do 算子的公式算出任意变量之间的因果作用。但是，在绝大多数的实际问题中，我们既不知道整个 DAG 的结构，也不能将所有的变量观测到。因此，仅仅有上面的公式是不够的。

下面，我将介绍 Judea Pearl 提出的“后门准则”（backdoor criterion）和“前门准则”（frontdoor criterion）。这两个准则的意义在于：（1）某些研究中，即使 DAG 中的某些变量不可观测，我们依然可以从观测数据中估计出某些因果作用；（2）这两个准则有助于我们鉴别“混杂变量”和设计观察性研究。

下面的讨论中，“可识别性”这个概念将被频繁的使用。因果推断中的识别性，和传统统计中的识别性定义是一致的。统计中，如果两个不同的模型参数，对应不同的观测数据的分布，那么我们称模型的参数可以识别。这里，如果因果作用可以用观测数据的分布唯一的表示，那么我们称因果作用是可以识别的。

前门准则和后门准则，都涉及了 d 分离（d-seperation）的概念。

定义（d 分离）: 设

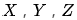是 DAG 中不相交的节点集合，

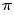为一条连接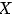

中某节点到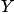

中某节点的路径（不管方向）。如果路径

上某节点满足如下的条件：

在路径上，w点处为v 结构（或称冲撞点，collider），且W及其后代不在Z中；
在路径上，w点处不是v 结构，且 w在中,

那么称Z阻断 (block) 了路径。

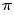进一步，如果 Z阻断了X到 Y的所有路径，那么称 z d 分离 X和Y，记为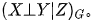

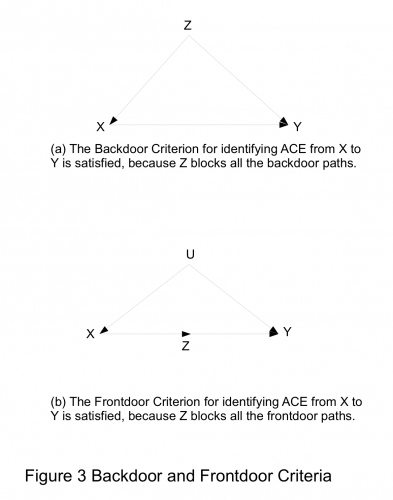
下面介绍 Pearl (1995) 的主要工作：后门准则和前门准则。

后门准则：在 DAG 中，如果如下条件满足：

Z中节点不能是的后代；
Z阻断了之间所有指向的路径（这样的路径可以称为后门路径）；

则称变量的集Z相对于变量的有序满足D对

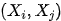后门准则。进一步，Z相对于变量的有序

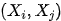满足后门准则，其中

是中的任意节点；那么称变量的集Z相对于节点集合的有序对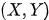

满足后门准则。

Pearl (1995) 证明，若存在一个变量集Z相对

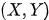满足后门准则，那X和Y的因果作用是可以识别的，且为了理解因果图的概念，下面的简短证明是很有必要的。

证明：在 Figure 3 (a) 中，

从上面可以看出，上面的后门准则和可忽略性假定下 ACE 的识别公式一样：都是用Z 做调整 (adjustment)，先分层再加权求和。这条结论在 Rosenbaum and Rubin (1983) 之后提出，且流行病学家也都用这样的调整方法控制混杂因素，因此对很多统计学家和流行病学家来说并不新奇。比较新颖的结论是下面的前门准则。

前门准则：在 DAG 中，称节点的集合Z 相对于有序对

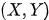满足前门准则，如果

Z切断了所有 X到Y 的直接路径；
X到Z 没有后门路径；
所有 Z到Y 的后门路径都被X 阻断。

此时，如果

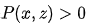X和Y的因果作用可识别，为

证明：Figure 3 (b) 中蕴含了条件独立性，将在推导中用到

。

这个前门路径看似很难理解，证明似乎很不直观，恰似变魔术。但是它其实是很显然的，在前门路径的 DAG 中，我们有：（1）X

Y

Z

Y

X

X

Y

Z

X

Y

Y的因果作用可识别——这样看来，这个结论就不奇怪了！

Pearl 在书中讲了一个非常有趣的例子，来说明前门准则的用处。

例子：我们关心吸X和肺之间的因果关系。由于一个潜在的不可观测的基因 U 的存在，吸烟和肺癌之间有一条“活”的后门路径，因此不借助其他的条件，我们无法识别吸烟与肺癌的因果关系。如果我们有这样的知识“吸烟X 仅仅通过肺部烟焦油的含量 Z来影响肺癌Y ”，那么吸烟对肺癌的因果作用就可以估计出来了。不过，这里需要两个条件，也就是在证明中使用的两个条件独立性，他们表明：（1）吸烟 X 和肺部烟焦油的含量 Z 之间没有“活”的后门路径（或者没有混杂因素）；（2）吸烟 X对肺癌Y 的作用仅仅来源于吸烟 X对肺部烟焦油 Z的作用，或者说，吸烟 X对肺癌Y 没有“直接作用”。

例子：在 Figure 1 的 DAG 中

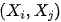之间的后门路径被

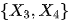或者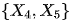

阻断，而前门路径被

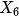阻断。上面的两个准则表明，要识别从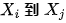的因果作用，我们不需要观测到所有的变量，只需要观测到切断后门路径或者前门路径的变量即可。

三、回到 Yule-Simpson’s Paradox

在第一节中，我们看到了经典的 Yule-Simpson’s Paradox。记T 为处理（吃药与否）；Y为结果（存活与否），X 是用于分层的变量（在最开始的例子中，X 是性别；在这里我们先将 X简单地看成某个用于分层的变量）。悖论存在，是因为T 和 Y正相关；但是按照X的值分层后， T和Y 负相关。分，还是不分？—–这是一个问题！这在实际应用是非常重要的问题。

不过，仅仅从“相关”（association）的角度讨论这个问题，是没有答案的。从“因果”（causation）的角度来看，才能有确切的回答。解释 Yule-Simpson’s Paradox，算是因果图的第一个重要应用。

下面，我将以上面的 Figure 4 中的四个图为例说明，三个变量之间的关系的复杂性。

图（a）：根据后门准则， X阻断了 T到Y 的后门路径，因此，根据 X做调整可以得到 T对Y的因果作用。如果实际问题符合图（a），那么我们需要用调整后的估计量。

图（b）：X是T的“后代”且是Y 的“父亲”。很多地方称，此时 X处于 T到Y 的因果路径上。直观的看，如果忽略X，那么 T和 Y之间的相关性就是 T对 Y的因果作用，因为 T和Y 之间的后门路径被空集阻断，我们无须调整。如果此时我们用X 进行调整，那么得到的是T 到Y 的“直接作用”。不过，什么是“直接作用”，我们将会在后面讨论；这里只是给一个形象的名字。

图（c）：和图（b）相同， T和Y 之间的相关性就是因果作用。但是，复杂性在于 X和Y 之间有一个共同的但是不可观测的原因U。此时，不调整的相关性，是一个因果关系的度量。但是，如果我们用X 进行调整，那么给定 X 后，T和 U相关，T和Y 之间的后门路径被打通，我们得到的估计量不再具有因果的含义。这种现象发生的原因是，

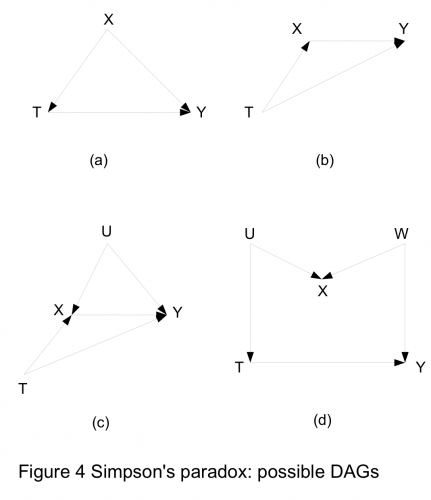
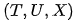之间形成了一个V结构：虽然 T和U之间是独立的，但是给定 X之后，T和U不再独立。

图（d）：这个图常常被 Judea Pearl 用来批评 Donald Rubin，因为它存在一个有趣的M 结构。在这个图中，由于 V结构的存在，T和Y 之间的后门路径被空集阻断，因此T 和 Y之间的相关性就是因果性。但是由于M 结构的存在，当我们用 X进行调整的时候， U和W 之间打开了一条“通路”（它们不再独立），因此 T和 Y之间的后门路径被打通，此时 T和Y 之间的相关性不再具有因果的含义。

我个人认为，因果图是揭开 Yule-Simpson’s Paradox 神秘面纱的有力工具。正如 Judea Pearl 在他的书中写到，不用因果的语言来描述这个问题，我们是讲不清楚这个悖论的。当然，因果的语言不止因果图，Judea Pearl 的解释始终不能得到 Donald Rubin 的认可。

四、讨论

用一个图来描述变量之间的因果关系，是很自然和直观的事情。但是，这并不意味着 Pearl 的理论是老妪能解的。事实上，这套基于 DAG 的因果推断的语言，比传统的 Neyman-Rubin 模型要晦涩很多。DAG 在描述因果关系的时候，常常基于很多暗含的假定而并不明说，这也是 DAG 并没有被大家完全接受的原因。传统的因果推断的语言，开始于 Jerzy Neyman 的博士论文；Donald Rubin 发展这套“潜在结果”的语言，并将它和缺失数据的理论联系在一起，成为统计界更多使用的语言。

在实际中，人们对于图模型的批评从未中断。主要的问题集中在如下的方面：

现实的问题，是否能用一个有向无环图表示？大多数生物学家看到 DAG 的反应是“能不能用图表示反馈？”的确，DAG 作为一种简化的模型，在复杂系统中可能不完全适用。要想将 DAG 推广到动态的系统，或者时间序列中，还有待研究。
Pearl 引入的 do 算子，是他在因果推断领域最主要的贡献。所谓 “do”，就是“干预”，Pearl 认为干预就是从系统之外人为的控制某些变量。但是，这依赖于一个假定：干预某些变量并不会引起 DAG 中其他结构的变化。这个假定常常会受到质疑，但是质疑归质疑，Pearl 的这个假定虽然看似很强，但根据观测数据却不可检验。这种质疑并不是 Pearl 的理论独有的缺陷，这事实上是一切研究的缺陷。比如，我们用完全随机化试验来研究处理的作用，我们要想将实验推广到观察性的数据或者更大的人群中去，也必须用到一些不可验证的假定。
很多人看了 Pearl 的理论后就嘲笑他：难道我们可以在 DAG 中干预“性别”？确实，离开了实际的背景，干预性别似乎是不太合理的。那这个时候，根据 Pearl 的 do算子得到的因果作用意味着什么呢？可以从几个方面回答这个问题。

很多问题，我们不能谈论“干预性别”，也不能谈论“性别”的“因果作用”。“性别”的特性是“协变量”（covariate），对于这类变量（如身高、肤色等），谈论因果作用不合适，因为我们不能想象出一个可能的“实验”，干预这些变量。
上面的回答基于“实验学派”（experimentalists’）的观点，认为不可干预，就没有“因果”。但是，如果认为只要有数据的生成机制，就有因果关系，那么算出性别的因果作用也不奇怪。（计量经就学一直有争议，以 Joshua Angrist、Guido Imbens 等为首的“实验派”，和以 James Heckman 为首的“结构方程模型”派，有过很激烈的讨论。）
有些问题中性别的因果作用是良好定义的。比如，我们可以人工的修改应聘者简历上的名字（随机的使用男性和女性名字），便可以研究性别对于求职的影响，是否存在性别歧视等等（已有研究使用过这种实验设计）。

一个更为严重的问题是，实际工作中，我们很难得到一个完整的 DAG，用于阐述变量之间的因果关系或者数据生成机制，使得 DAG 的应用受到的巨大的阻碍。不过，从观测数据学习 DAG 的结构，确实是一个很有趣且重要的问题，这留待下回分解。

在结束时，留些一些思考的问题：

在何种意义下，后门准则的条件，等价于可忽略性，即?
在第一节的 Yule-Simpson’s Paradox 中，我们最终选择调整的估计量，还是不调整的估计量？

6. 因果推断简介之六：

工具变量（instrumental variable）

为了介绍工具变量，我们首先要从线性模型出发。毫无疑问，线性模型是理论和应用统计（包括计量经济学和流行病学等）最重要的工具；对线性模型的深刻理解，可以说就是对一大半统计理论的理解。下面的第一部分先对线性模型，尤其是线性模型背后的假设做一个回顾。

一、线性回归和最小二乘法

线性模型和最小二乘的理论起源于高斯的天文学研究，“回归”（regression）这个名字则是 Francis Galton 在研究优生学的时候提出来的。为了描述的方便，我们假定回归的自变量只有一维，比如个体 ii 是否接受某种处理（吸烟与否；参加某个工作；等等），记为 Di。回归的因变量也是一维，表示我们关心的结果（是否有肺癌；是否找到工作培训与否；等等），记为Yi。假定我们的研究中有 n 个个体，下面的线性模型用于描述 D 和 Y 之间的 “关系”：

一般情形下，我们假定个体间是独立的。模型虽简单，我们还是有必要做一些解释。首先，我们这里的讨论都假定 Di 是随机变量，对应统计学中的随机设计（random design）的情形；这和传统统计学中偏好的固定设计（fixed design）有点不同—那里假定 Di总是固定的。（统计学源于实验设计，那里的解释变量都是可以控制的，因此统计学教科书有假定固定设计的传统。）假定 Di是随机的，既符合很多社会科学和流行病学的背景，又会简化后面的讨论。另外一个问题是 εi，它到底是什么含义？Rubin 曾经嘲笑计量经济学家的 εi道：为了使得线性模型的等式成立，计量经济学家必须加的一项，就叫 εi。批评的存在并不影响这个线性模型的应用；关键的问题在于，我们在这个 εi上加了什么假定呢？最根本的假定是：

不同的教科书稍有不同，比如 Wooldridge 的书上假定E(εi∣Di)=0，很显然，这蕴含着上面两个假定。零均值的假定并不强，因为 αα“吸收”了 εiεi的均值；关键在第二个协方差为零的假定—它通常被称为 “外生性”（exogeneity）假定。在这个假定下，我们在 (1) 的两边关于 Di 取协方差，便可以得到：

cov(Yi,Di)=βvar(Di),

因此，β=cov(Yi,Di)/var(Di)，我们立刻得到了矩估计：

上面的估计式也是通常的最小二乘解，这里只是换了一个推导方式。如果将 (1) 看成一个数据生成的机制，在假定 (2) 下我们的确可以估计出因果作用 β.

二、内生性和工具变量

问题的关键是假定 (2) 很多时候并不成立（cov(Di,εi)≠0），比如，吸烟的人群和不吸烟的人群本身很不相同，参加工作培训的人可能比不参加工作培训的人有更强的找工作动机，等等。因此，包含个体 ii其他所有隐藏信息的变量 εiεi不再与 DiDi不相关了—这被称为 “内生性”（endogeneity）。这个时候，最小二乘估计收敛到 β+cov(D,ε)/var(D), 因而在 cov(D,ε)≠0时不再是β的相合估计。

前面几次因果推断的介绍中提到，完全的随机化实验，可以给我们有效的因果推断。但是很多问题中，强制性的随机化实验是不现实或者不符合伦理的。比如，我们不能强制某些人吸烟，或者不吸烟。但是，“鼓励性实验”依然可行。我们可以随机地给吸烟的人以某种金钱的奖励，如果他们放弃吸烟，则获得某种经济上的优惠。将这个 “鼓励性” 的变量记为 Zi，它定义为是否被鼓励的示性变量，取值 0-1。由于我们的鼓励是完全随机的，有理由假定 cov(Zi,εi)=0。

以上的各个假定，可以用下面的一个图来形象的描述。

如图所示，由于DD和YY之间存在一个混杂因素UU，两者之间的因果作用是不可以用线性回归相合估计的。工具变量ZZ的存在，使得DD到YY的因果作用的识别成为了可能。这里的工具变量ZZ满足如下的条件: Z⊥U,Z⊥DZ⊥U,Z⊥̸D，并且 Z⊥Y|(D,U)Z⊥Y|(D,U)。第三个条件，可以理解成为 “无 Z到 Y的直接作用”。

此时，我们在线性模型 (1) 两边关于 Zi 取协方差，得到

cov(Zi,Yi)=βcov(Zi,Di)

因此，

β=cov(Zi,Yi)cov(Zi,Di)，我们立刻得到如下的矩估计：

根据大数定律，这个 “工具变量估计” 是 β的相合估计量。上面的式子对一般的 Zi都是成立的；当 Zi是 0-1 变量时，上面的式子可化简成：

其中Y¯1表示 Zi=1组的平均结果，Y¯1表示 Zi=0组的平均结果，关于 DD的定义类似。上面的估计量，很多时候被称为 Wald 估计量（它的直观含义是什么呢？）需要注意的是，(3) 要求 cov(Zi,Di)≠0，即 “鼓励” 对于改变人的吸烟行为是有效的；否则上面的工具变量估计量在大样本下趋于无穷大。

三、潜在结果视角下的因果作用

工具变量估计量在文献中存在已有很多年了，一直到了 Angrist, Imbens and Rubin (1996) 年的文章出现，才将它和潜在结果视角下的因果推断联系起来。关于 Neyman 引进的潜在结果，需要回顾这一系列的第二篇文章。

一般地， Z 表示一个 0-1 的变量，表示随机化的变量（1 表示随机化分到非鼓励组；0 表示随机化分到鼓励组）；D 表示最终接受处理与否（1 表示接受处理；0 表示接受对照）；Y 是结果变量。为了定义因果作用，我们引进如下的潜在结果：(Yi(1),Yi(0)) 表示个体 i 接受处理和对照下 Y 的潜在结果；(Di(1),Di(0)) 表示个体 i 非鼓励组和鼓励组下 D 的潜在结果。由于随机化，下面的假定自然的成立：

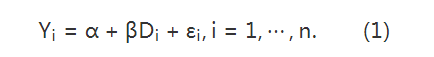
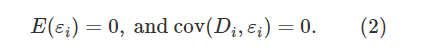
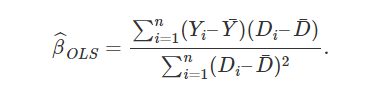
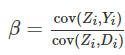
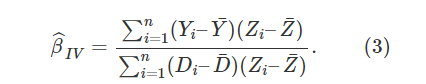
（随机化）Zi⊥{Di(1),Di(0),Yi(1),Yi(0)}.

根据鼓励性实验的机制，个体在受到鼓励的时候，更加不可能吸烟，因为下面的单调性也是很合理的：

（单调性）Di(1)≤Di(0).

由于个体的结果 YY 直接受到所受的处理 DD 的影响，而不会受到是否受鼓励 ZZ 的影响，下面的排除约束（exclusion restriction）的假定，很多时候也是合理的：

（排除约束）Di(1)=Di(0) 蕴含着 Yi(1)=Yi(0).

上面的假定表明，当随机化的 “鼓励”ZZ 不会影响是否接受处理 DD时，随机化的 “鼓励” ZZ 也不会影响结果变量 YY。也可以理解成，随机化的 “鼓励” ZZ 仅仅通过影响是否接受处理 DD 来影响结果 YY，或者说，随机化 “鼓励” ZZ 本身对与结果变量 YY没有“直接作用”。

以上三个假定下，我们得到：

单调使得 D 的潜在结果的组合只有三种；排除约束假定使得上面分解的后两个式子为0。由于对于(Di(1)=0,Di(0)=0) 和(Di(1)=1,Di(0)=1)两类人，随机化的 “鼓励” 对于 D的作用为 0，(Di(1)=1,Di(0)=0)一类人的比例就是Z对D平均因果作用：ACE(Z→D)=P{Di(1)=1,Di(0)=0}. 因此，

上面的式子被定义为 CACE 是有理由的。它表示的是子总体 (Di(1)=1,Di(0)=0) 中，随机化对于结果的因果作用；由于这类人中随机化和接受的处理是相同的，它也表示处理对结果的因果作用。这类人接受处理与否完全由于是否接受鼓励而定，他们被成为 “依从者”（complier），因为这类人群中的平均因果作用又被成为 “依从者平均因果作用”（CACE：complier average causal effect）; 计量经济学家称它为 “局部处理作用”（LATE：local average treatment effect）

由于ZZ是随机化的，它对于DD和YY的平均因果作用都是显而易见可以得到的。

因为

CACE 的一个矩估计便是

由此可见工具变量估计量的因果含义。上面的讨论既显示了工具变量对于识别因果作用的有效性，也揭示了它的局限性：我们只能识别某个子总体的平均因果作用；而通常情况下，我们并不知道某个个体具体属于哪个子总体。

四、实例

这部分给出具体的例子来说明上述理论的应用，具体计算用到了第五部分的一个函数（其中包括用 delta 方法算的抽样方差）。这里用到的数据来自一篇政治学的文章 Green et al. (2003) “Getting Out the Vote in Local Elections: Results from Six Door-to-Door Canvassing Experiments”，数据点击此处可以在此下载。

文章目的是研究某个社会实验是否能够提高投票率，实验是随机化的，但是并非所有的实验组的人都依从。因此这里的变量 ZZ 表示随机化的实验，DD 表示依从与否，YY 是投票与否的示性变量。具体的数据描述，可参加前面提到的文章。

原始数据总结如下：

根据下一个部分的函数，我们得到如下的结果：


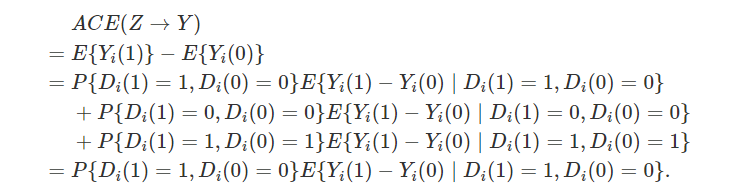
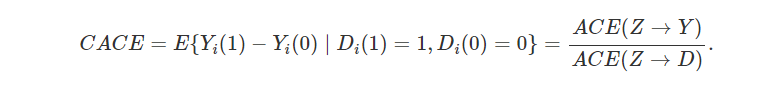
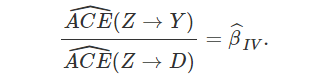
CACE.IV(Y, D, Z)$CACE[1] 0.07914375
$se.CACE           [,1][1,] 0.02273439
$p.value             [,1][1,] 0.0004991073
$prob.complier[1] 0.2925123
$se.complier[1] 0.004871619

由此可见，这个实验对于提高投票率，有显著的作用。

五、R code

## function for complier average causal effectCACE.IV <- function(outcome, treatment, instrument) {  Y <- outcome  D <- treatment  Z <- instrument  N <- length(Y)
  Y1 <- Y[Z == 1]  Y0 <- Y[Z == 0]  D1 <- D[Z == 1]  D0 <- D[Z == 0]
  mean.Y1 <- mean(Y1)  mean.Y0 <- mean(Y0)  mean.D1 <- mean(D1)  mean.D0 <- mean(D0)
  prob.complier <- mean.D1 - mean.D0  var.complier <- var(D1) / length(D1) + var(D0) / length(D0)  se.complier <- var.complier^0.5
  CACE <- (mean.Y1 - mean.Y0) / (mean.D1 - mean.D0)
  ## COV  pi1 <- mean(Z)  pi0 <- 1 - pi1
  Omega <- c(    var(Y1) / pi1, cov(Y1, D1) / pi1, 0, 0,    cov(Y1, D1) / pi1, var(D1) / pi1, 0, 0,    0, 0, var(Y0) / pi0, cov(Y0, D0) / pi0,    0, 0, cov(Y0, D0) / pi0, var(D0) / pi0  )  Omega <- matrix(Omega, byrow = TRUE, nrow = 4)
  ## Gradient  Grad <- c(1, -CACE, -1, CACE) / (mean.D1 - mean.D0)
  COV.CACE <- t(Grad) %*% Omega %*% Grad / N
  se.CACE <- COV.CACE^0.5
  p.value <- 2 * pnorm(abs(CACE / se.CACE), 0, 1, lower.tail = FALSE)
  ## results  res <- list(    CACE = CACE,    se.CACE = se.CACE,    p.value = p.value,    prob.complier = prob.complier,    se.complier = se.complier  )
  return(res)}

7. 因果推断简介之七：Lord’s Parado

在充满随机性的统计世界中，悖论无处不在。这一节介绍一个很有名，但是在中文统计教科书中几乎从未介绍过的悖论。这个悖论是 Educational Testing Service (ETS) 的统计学家 Frederic Lord 于 1967 年提出来的；最终由同在 ETS 工作的另外两位统计学家 Paul Holland 和 Donald Rubin 于 1982 年圆满地找出了这个悖论的根源。这部分先介绍这个悖论，再介绍 Holland 和 Rubin 的解释，最后是一些结论。

一、Lord's Paradox

考虑下面一个简单例子，具体的数字是伪造的。某个学校想研究食堂对于学生体重是否有差异性的影响，尤其关心食堂对于男女学生体重影响是否相同。于是统计学家们收集了如下的数据：学生的性别GG；学生在 1963 年 6 月入学时候的体重XX；学生在 1964 年 6 月放暑假时候的体重YY。

第一个统计学家，采取了一种很简单的方法。如图所示，横轴表示 1963 年 6 月入学前的体重X，纵轴表示 1964 年 6 月前放假的体重Y。个体上来看，男女入学前和入学后一年体重都会有些变化，男女学生体重的散点图分别用绿色和红色标出。从男女学生生平均体重来看，男生入学前后一年平均体重均是 150 磅（图中右上角的黑点），女生入学前后一年平均体重均为 130 磅（图中左下角的黑点）。图中的虚线是对角线Y=X，两个黑点均位于对角线上。因此，第一个统计学家的结论是食堂对于男女学生体重都没有影响，因此对男女学生体重的作用相同。

注：横轴表示 1963 年 6 月入学前的体重X，纵轴表示 1964 年 6 月前放假的体重Y；虚线是对角线Y=X；男女学生体重的散点图分别用绿色和红色标出。图中数据生成机制如下：男学生(X,Y)~二元正态分布，均值(150,150)，协方差矩阵;女学生(X,Y)~二元正态分布，均值(130,130)，协方差矩阵。生成这幅图的 R 代码可以在这里下载：Rcodehttps://uploads.cosx.org/2013/09/Rcode2.txt。由于样本量 3000，样本均值非常接近理论均值，因此落在了对角线上。)(150,150)生成这幅图的 R 代码可以在这里下载：Rcode。由于样本量 3000，样本均值非常接近理论均值，因此落在了对角线上。)

第二个统计学家，由于受到了高等的统计训练，知道 R A Fisher 的 Analysis of Covariance (ANCOVA) ，提出了更加复杂的方法。他认为，我们的分析应该控制入学前的体重，做如下的线性回归：

他进一步认为，上面线性回归的系数 βgβg 反应的就是男女的差别。用最小二乘法拟合上面的回归模型，等价于在男女学生中拟合两条平行的回归直线。如图所示，两条直线斜率 βxβx 相同，但是截距不同，截距之差就是回归系数ˆβg=6.34β^g=6.34。结论是，食堂对于男女体重有差别性的影响。

这两位统计学家得到了不同的结论，究竟谁对谁错呢？Lord 称这个现象为悖论，那么悖论的根源是什么呢？

二、悖论的根源：因果推断视角下的解释

要想解释这个悖论，使用线性回归模型益处不大，因为究竟能否将回归系数解释成因果作用，是个根本性的问题。在下面的讨论中，我们假定数据的样本量足够大，因而可以忽略小样本带来的随机性；也可以认为整个讨论都在总体上进行。和前面一样，我们用Gi表示个体i的性别，男性取值为 1，女性取值为 0；Xi是个体 i在 1963 年 9 月的体重。由于这两个变量都发生在接受处理（在食堂进餐与否）之前，它们都可以看成是协变量，不受处理的影响。我们采用潜在结果模型，定义 { Yi(1), Yi(0) } 是个体 $i$ 在食堂进餐和不在食堂进餐下于 1964 年六月体重的潜在结果。

如果用T表示在食堂进餐与否的变量，那么每个学生都是T=1。当写下潜在结果之后，我们就发现问题的根源之一，是整个研究根本不存在对照组（全体学生其实都在食堂进餐），每个个体在 1964 年 6 月都取值Y(1)(也就是前面的记号Y)。

食堂对于男女学生体重平均因果作用的差是：

上面的推导虽然简单，但是将 ΔΔ 分成了两个显著不同的部分：第一个方括号内的项是我们能够从观测数据中得到的；第二个方括号中的项是我们不可观测的，因为没有任何一个学生接受了食堂之外的处理。

如果我们假定 Y(0)=XY(0)=X，也就是说如果学生不来食堂进餐，他们的体重将和入学前一样，那么

根据上面的图和统计学家一的推理逻辑，我们知道Δg=0(g=0,1)Δg=0(g=0,1)

（男女学生的体重不受处理影响），那么Δ=0Δ=0（处理对于男女体重没有差异性的影响）。在这个假定下，第一个统计学家的断言是正确的。

显然，假定 Y(0)=XY(0)=X是无法被数据证明或者证伪的，它只能依赖于我们的先验知识。那么在什么假定下，第二个统计学家又是对的呢？

根据第二个统计学家做 ANCOVA 的逻辑，他可以假定

并且把δ=a1–a0δ=a1–a0

当成食堂对于男女体重差异作用的度量。δδ 其实就是上面的线性回归模型(∗)的回归系数 βg。如果我们假定 Y(0)=α+bXY(0)=α+bX，那么不去食堂进餐时的潜在体重Y(0)是入学前体重 XX 的线性函数且截距是 bb；这表明Y(1)Y(1) 和 Y(0) 关于 XX 的模型，仅仅截距不同，斜率相同。这个假定并非不可能。此时，

最后一行等于 δδ，因为根据条件期望的性质，方括号中的两项分别是 a1a1 和 a0a0：

这样一来，第二个统计学家的结论就是正确的。

三、结论

根据上面的讨论，关于 Lord’s Paradox，我们有如下的结论：

（1）Lord’s Paradox 的根源在于，整个研究没有对照组；我们甚至不知道什么是对照组，不在食堂进餐，是在家里进餐，还是外面的参观进餐，还是其他？这其实导致 $Y(0)$ 并非完好定义。上面的讨论则是假定 Y(0)Y(0)是良好定义的。

（2）回归或者协方差分析等统计工具，并不能清楚的回答因果的问题。这个问题中，ΔΔ是一个我们关心的因果度量，离开潜在结果，是很难定义的。根据上面的讨论，两位统计学家不采用潜在结果模型，甚至没有意识到，这个研究根本的问题在于缺少对照。

当然，如果我们能够做一个随机化的实验，有处理和对照组，那么回归分析也可能得到合理的答案。

（3）统计学家一和二，都可以是对的。他们结论的正确性，依赖于不同的假定；而这些假定本身是不可能被检验的。

（5）统计学家一和二，都是错的。他们有结论，但是却从未清楚地陈述结论回答的是什么问题。

（6）R A Fisher 在实验设计中提出了 ANCOVA，但是这个方法不是万能的。事实上，这个方法导致的问题，比它带来的功用更严重；这点以后再说。

8. 因果推断简介之八：

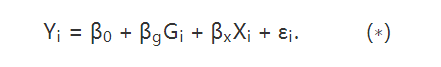
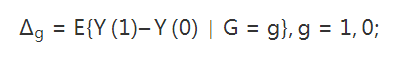
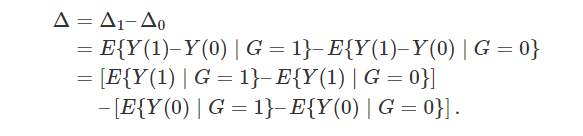
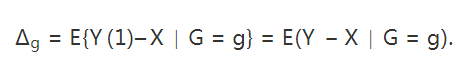
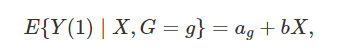
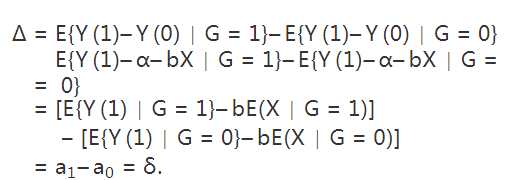
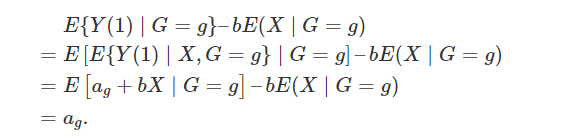
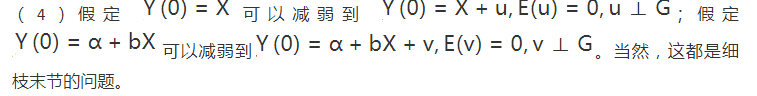
吸烟是否导致肺癌？Fisher versus Cornfield

这一节介绍一个有趣的历史性例子：吸烟是否导致肺癌？主要涉及的人物是 R A Fisher 和 J Cornfield。前者估计上这个网站的人都听过，后者就显得比较陌生了。事实上，Cornfield 在统计、生物统计和流行病学都有着非常重要的贡献。来自 Wikipedia 的一句介绍：“He was the R. A. Fisher Lecturer in 1973 and President of the American Statistical Association in 1974.” 虽然 Cornfield 和 Fisher 学术观点不同（本节介绍），但是 Cornfield 还是在 1973 年给了 Fisher Lecture。

下面我们先介绍 Fisher 和 Cornfield 关于观察性研究中因果推断的两种观点，再给出技术性的细节。

一、Cornfield 条件或者 Cornfield 不等式

（图注：R A Fisher）

我先陈述 Fisher 的观点。由于 Yule-Simpson Paradox 的存在，即使我们观测到吸烟和肺癌之间的正相关关系，也不能断定它们之间有因果性。可能存在一个未观测的基因，它既使得某些人更可能吸烟，又使得这些人更可能患肺癌。因此，即使吸烟和肺癌没有因果关系，这个未观测的基因也可能导致吸烟和肺癌是正相关的。关于 Yule-Simpson Paradox，这一系列的第一篇有介绍。Fisher 的观点可以用一个有向无环图（DAG）来表示：

图中，吸烟到肺癌没有直接的边，因此吸烟对肺癌的因果作用是 0。但是由于它们之间存在一个共同原因 “hidden gene”，它们是相关的。我们用 E 表示是否吸烟 (1= 是，0=否)；D 表示是否患肺癌 (1=是，0=否)；U 表示是否有某种基因 (1= 是，0= 否)。这个符号系统在流行病学比较常用，因为 E 表示暴露与否（exposure），D表示疾病（disease），U表示未观测的混杂因素（unobservable confounder）。在 Fisher 的时代，研究者通过收集的大量数据，得到吸烟对于肺癌的相对风险（relative risk；或称风险比，risk ratio；都简写成 RR）是

流行病学家关心这个 RRED 是否表明了吸烟和肺癌的因果关系。Fisher 表示否定。从一个悲观的角度来讲，我们确实不能从相关关系得到因果性；Fisher 如果表示怀疑，假定有一个未观测的基因，也是无可反驳的。Fisher 的这个说法有时也被称为 “共同原因” 假说。Cornfield 则采取了一个不太悲观的角度。他问：如果 Fisher 的 “共同原因” 假说是对的，那么 E 和 U 之间的相关关系需要多强，才能导致 RRED=9，即 “吸烟患肺癌” 是“不吸烟患肺癌”的风险的 99 倍呢？如果 E和 U之间的相关关系强到不具有生物学意义（E与 U 的相对风险值大得在现实中不太可能），那么 Fisher 的 “共同原因” 假说就不成立，更大的可能性是吸烟 E 对肺癌 D 有因果作用。

那么 Cornfield 是如何有力反驳 Fisher 的观点的呢？

（图注：J Cornfield）

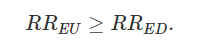
Cornfield 通过简单的数学证明，得到了如下的不等式，文献中也称为 Cornfield 不等式：

也就是说，如果 Fisher 的 “共同原因” 假说成立，那么 E 和 U 之间的 RR 必将大于 E 和 D 之间的 RR。在吸烟和肺癌的例子中，RREU≥9。RREU≥9，即 P(U=1|E=1)/P(U=1|E=0)≥9，直观解释就是 “吸烟时有某个基因 U 存在” 的概率是 “不吸烟时有某个基因 U 存在” 的概率的 9 倍多。根据 Cornfield 进一步的逻辑，由于吸烟更多的是一个社会性的行为，很难想象吸烟的行为能够对于某个基因的存在与否有着 9 倍的预测能力。我前段时间问身边一个生物的 PhD，你觉得 RREU≥9 可能吗？他的回答是不太可能，理由也是说，吸烟更多的决定于社会经济地位、家庭背景等变量，和基因也许有关系，但是不会强到 RREU≥9 的程度。Cornfield et al. (1959) 的原话是：

… if cigarette smokers have 9 times the risk of nonsmokers for developing lung cancer, and this is not because cigarette smoke is a causal agent, but only because cigarette smokers produce hormone X, then the proportion of hormone-X producers among cigarette smokers must be at least 9 times greater than nonsmokers. If the relative prevalence of hormone-X-producers is considerably less than ninefold, then hormone-X cannot account for the magnitude of the apparent effect.

如果我们相信 Cornfield 的逻辑， RREU≥9 在生物学意义上不太可能，那么 Fisher 的 “共同原因” 假说就不成立，吸烟对肺癌的确存在因果作用；反映到上面的DAG 上，吸烟 EE 到肺癌 DD 有一条直接的边。

Cornfield 的这项简单研究，开始了流行病学和统计学中敏感性分析的研究；比如 Rubin 和 Rosenbaum 很多工作都是在 Cornfield 的启发下做出来的。简单地说，敏感性分析，就是在朝着 Yule-Simpson Paradox 的反方向进行的：复杂虽然总是存在，但是我们相信这个世界并不是疯狂的复杂。

二、技术细节

这一部分我们给出 Cornfield 不等式的证明。虽然证明不难，但是想想 Cornfield 于 1959 年用这样一个简单的不等式来反驳 Fisher，就觉得它的历史意义还是不小的。当然不关心技术细节的读者，可以直接忽略本节。关心技术细节的读者，下面的证明虽然冗长，但是只用到非常初等的数学（也许它可以作为一道初等概率论的习题）。

为了简化证明，我们引进一些记号：

不妨假设 RRED≥1 并且 RREU≥1；若不成立，我们总可以重新对这些二值变量的 0 和 1 类进行重新定义。首先，我们在条件独立性 E⊥D|U 下得到 RRED的等价表示：

条件 RREU≥1等价于 f1≥f0，因此，上面 RRED是关于 RRUD的单调递增函数。进一步，

由此，Cornfield 不等式得证。

参考文献

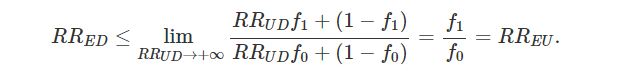
Bickel, P. J. and Hammel, E. A. and O’Connell, J. W. (1975) Sex bias in graduate admissions: Data from Berkeley. Science, 187, 398-404.
Pearl, J. (2000) Causality: models, reasoning, and inference. Cambridge University Press。
Rosenbaum, P.R. and Rubin, D.B. (1983) The central role of the propensity score in observational studies for causal effects. Biometrika, 70, 41-55.
Rothman, K., Greenland, S. and Lash, T. L. (2008) Modern Epidemiology. Lippincott Williams & Wilkins.
Neyman, J. (1923) On the application of probability theory to agricultural experiments. Essay on principles. Section 9. reprint in Statistical Science. 5, 465-472.
Pearl, J. (1995) Causal diagrams for empirical research. Biometrika, 82, 669-688.
Pearl, J. (2000) Causality: models, reasoning, and inference. Cambridge University Press。
Rubin, D.B. (1978) Bayesian inference for causal effects: The role of randomization. The Annals of Statistics, 6, 34-58.
Neyman, J. (1923) On the application of probability theory to agricultural experiments. Essay on principles. Section 9. reprint in Statistical Science. 5, 465-472. with discussion by Donald Rubin.
Rosenbaum, P. R. and Rubin, D. B. (1983) The central role of the propensity score in observational studies for causal effects. Biometrika, 70, 41-55.
Rubin, D. B. (1976) Inference and missing data (with discussion). Biometrika, 63, 581-592.
Rubin, D. B. (1978) Bayesian inference for causal effects: The role of randomization. The Annals of Statistics, 6, 34-58.
Wooldridge, J. M. (2002) Econometric analysis of cross section and panel data. The MIT press.
Lord FM. A paradox in the interpretation of group comparisons. Psychol Bull. 1967;68:304–5. doi: 10.1037/h0025105.
Holland, P.W., Rubin, D.B. (1983). On Lord’s paradox. In: Wainer, H., Messick, S. (Eds.), Principals of Modern Psychological Measurement. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 3–25.
Cornfield 最早的论文发表于 1959 年；由于它的重要性，这篇文章又在 2009 年重印了一次（50 周年纪念）。于是参考文献有两篇，它们是一样的；不过后者多了很多名人的讨论。
Cornfield J et al. Smoking and lung cancer: recent evidence and a discussion of some questions. JNCI 1959;22:173-203.
Cornfield J et al. Smoking and lung cancer: recent evidence and a discussion of some questions. Int J Epidemiol 2009;38:1175-91.（本文邀请了 David R Cox 和 Joel B Greenhouse 等人讨论。）
最近 Ding and VanderWeele 重新回访了这个经典问题，给出了更加广泛的结果。Ding, Peng and Vanderweele, Tyler J. (2014). Generalized Cornfield conditions for the risk difference, Biometrika, 101:4, 971-977. https://doi.org/10.1093/biomet/asu030

作者简介

丁鹏，2004 年至 2011 年在北京大学数学科学学院获得本科和硕士学位，2015 年获哈佛大学统计学博士学位，2016 年起任教于加州大学伯克利分校统计系，2021 年晋升为副教授。其主要研究方向是因果推断。

编辑：于腾凯

校对：林亦霖

丁鹏：多角度回顾因果推断的模型方法

1. 因果推断简介之一：从 Yule-Simpson’s Paradox 讲起

2. 因果推断简介之二：Rubin Causal Model (RCM) 和随机化试验

3. 因果推断简介之三：R. A. Fisher 和 J. Neyman 的分歧