期望最大化（Expectation Maximization）算法简介和Python代码实现（附代码）

来源：DeepHub IMBA
本文约3400字，建议阅读5分钟
本文中通过几个简单的示例解释期望最大化算法是如何工作的。

期望最大化（EM）算法被广泛用于估计不同统计模型的参数。它是一种迭代算法，可以将一个困难的优化问题分解为几个简单的优化问题。在本文中将通过几个简单的示例解释它是如何工作的。

这个算法最流行的例子（互联网上讨论最多的）可能来自这篇论文

（http://www.nature.com/nbt/journal/v26/n8/full/nbt1406.html）。这是一个非常简单的例子，所以我们也从这里开始。

假设我们有两枚硬币（硬币 1 和硬币 2），正面朝上的概率不同。我们选择其中一枚硬币，翻转 m=10 并记录正面的数量。假设我们重复这个实验 n=5 次。我们的任务是确定每个硬币正面朝上的概率。我们有：

首先假设我们知道每个实验中使用了哪种硬币。在这种情况下，有完整的信息，可以使用最大似然估计 (MLE) 技术轻松求解 p_1 和 p_2。首先计算似然函数并取其对数（因为最大化对数似然函数更容易）。由于我们有 n 个独立实验，似然函数只是在 x_i 处评估的个体概率质量函数 (PMF) 的乘积（数字是实验 i 中的正面）。

现在我们需要最大化关于概率 p_1 和 p_2 的对数似然函数。它可以在数值上或解析上完成。我将演示这两种方法。首先让我们尝试解决它，可以分别求解 p_1 和 p_2。

对 p_1 取对数似然函数的导数，将其设置为零并求解 p_1。当区分对数似然函数时，涉及 p_2 的项的导数将等于 0。所以我们只使用涉及硬币 1 的实验数据。

得到的答案很直观：它是我们在硬币 1 的实验中得到正面的总数除以硬币 1 的实验中的翻转总数。p_2 的计算将是类似的。

现在我将在 Python 中实现这个解决方案。

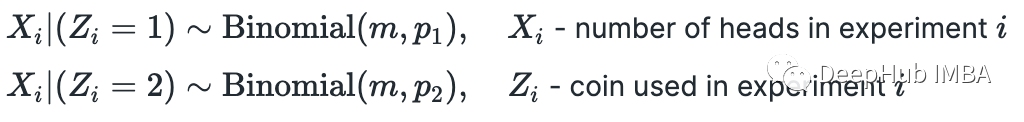
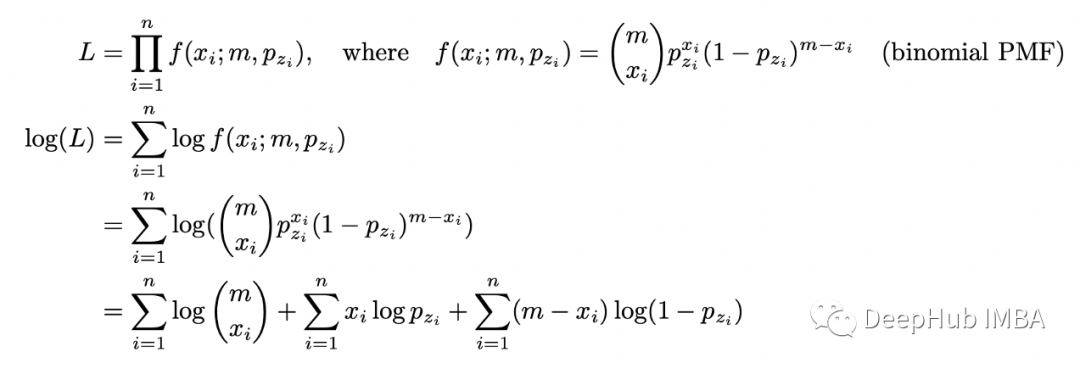
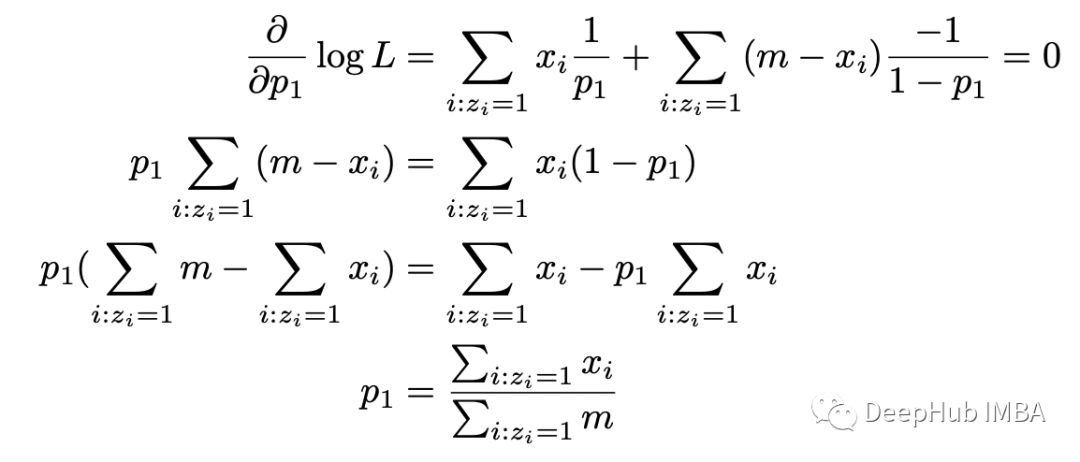
m = 10 # number of flips in experimentn = 5 # number of experiments
p_1 = 0.8p_2 = 0.3
xs = [] # number of heads in each experimentzs = [0,0,1,0,1] # which coin to flip
np.random.seed(5)for i in zs:  if i==0:      xs.append(stats.binom(n=m, p=p_1).rvs()) # flip coin 1  elif i==1:      xs.append(stats.binom(n=m, p=p_2).rvs()) # flip coin 2       xs = np.array(xs)print(xs)
exp1 = [0,1,3] # indexes of experiments with coin 1exp2 = [2,4] # indexes of experiments with coin 2
print('Analytical solutions:')print('p1: ', xs[exp1].sum() / (m * len(exp1)))print('p2: ', xs[exp2].sum() / (m * len(exp2)))

这些实现都比较简单。我们只是实现上面计算的公式并插入数字。运行此代码的结果如下所示。

解决这个问题的另一种方法是使用数值求解器。我们需要找到一个最大化对数似然函数的解决方案，当使用数值求解器时，不需要计算导数并手动求解最大化对数似然函数的参数。只需实现一个我们想要最大化的函数并将其传递给数值求解器。

由于 Python 中的大多数求解器旨在最小化给定函数，因此我们实现了一个计算负对数似然函数的函数（因为最小化负对数似然函数与最大化对数似然函数相同）。

代码和结果如下所示。

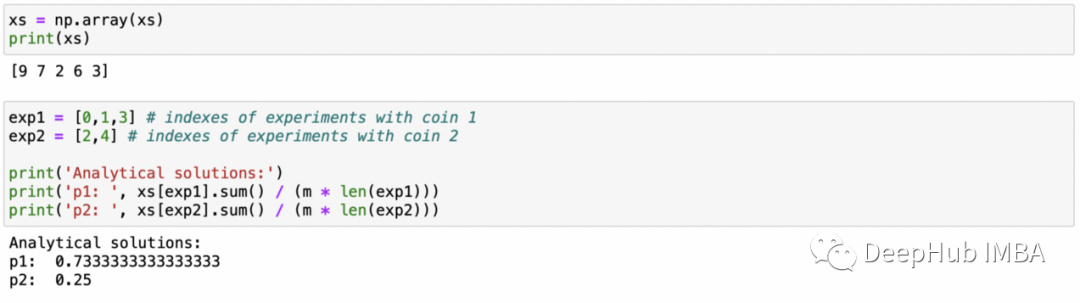
ef neg_log_likelihood(probs, m, xs, zs):  '''  compute negative log-likelihood  '''  ll = 0  for x,z in zip(xs,zs):      ll += stats.binom(p=probs[z], n=m).logpmf(x)         return -ll res = optimize.minimize(neg_log_likelihood, [0.5,0.5], bounds=[(0,1),(0,1)], args=(m,xs,zs), method='tnc')
print('Numerical solution:')print('p1: ', res.x[0])print('p2: ', res.x[1])

和上面的第一种方法得到与解析解相同的结果。

现在假设我们不知道每个实验中使用了哪种硬币。在这种情况下，变量 Z 没有被观察到（它被称为潜在变量或隐藏变量）并且数据集变得不完整。现在估计概率 p_1 和 p_2 变得更加困难，但仍然可以在 EM 算法的帮助下完成。

如果知道选择硬币 1 或硬币 2 的概率，就可以使用贝叶斯定理来估计每个硬币的偏差。

如果知道每个硬币的偏差，可以估计在给定的实验中使用硬币 1 或硬币 2 的概率。在 EM 算法中，我们对这些概率进行初步猜测，然后在两个步骤之间迭代（估计偏差给定使用每个硬币的概率和估计使用每个硬币给定偏差的概率）直到收敛。可以在数学上证明这种算法收敛到（似然函数的）局部最大值。

现在尝试复制论文中提供的示例。问题设置如下所示。

完整的数据集由两个变量 X 和 Z 组成，但仅观察到 X。由于随机选择两个硬币中的一个，因此选择每个硬币的概率等于 0.5。为了求解 theta，我们需要最大化以下似然函数：

上述函数称为不完全似然函数。如果我们计算它的对数，我们得到：

对数下的求和使最大化问题变得困难。

让我们将隐藏变量 Z 包含在似然函数中以获得完全似然：

完全似然函数的对数为：

这样就没有对数内的求和，更容易解决这个函数的最大化问题。由于没有观察到 Z 的值，所以不能直接计算和最大化这个函数。但是如果我们知道 Z 的分布，就可以计算其期望值并使用它来最大化似然（或对数似然）函数。

这里的问题是，要找到 Z 的分布，需要知道参数 theta，而要找到参数 theta，需要知道 Z 的分布。EM 算法允许我们解决这个问题。我们从参数 theta 的随机猜测开始，然后迭代以下步骤：

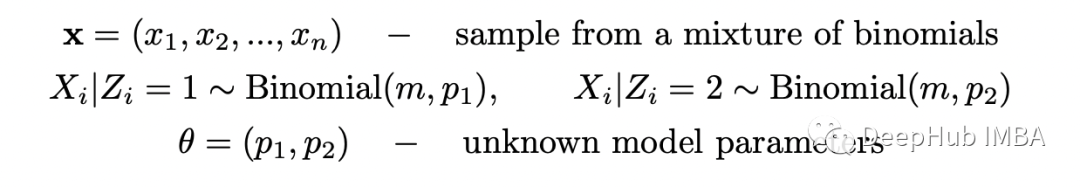
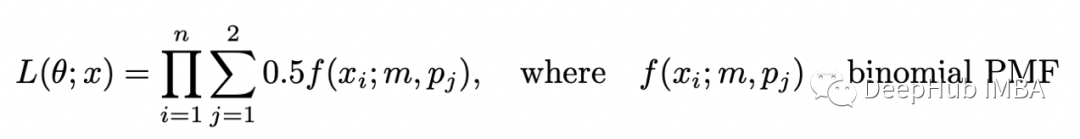
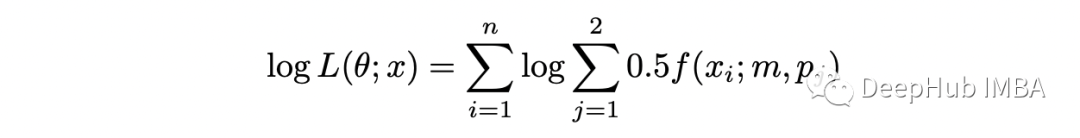
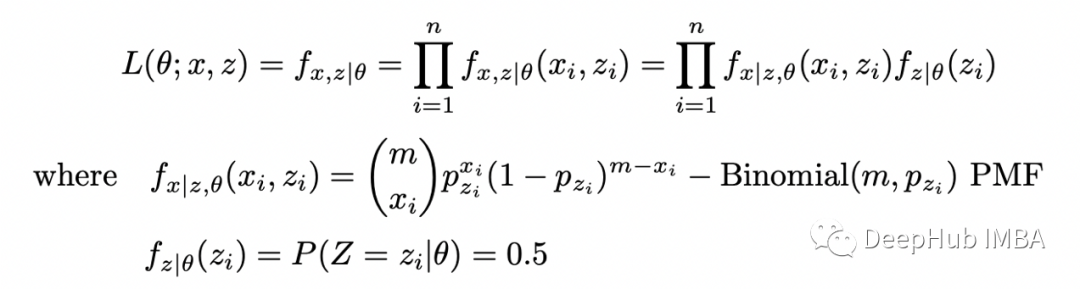
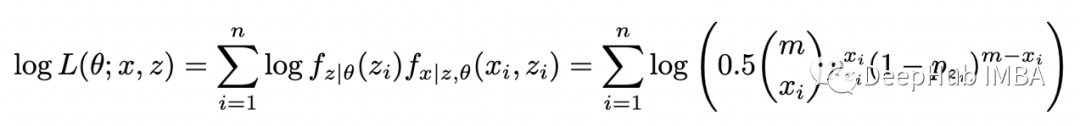
1. 期望步骤（E-step）：计算完整对数似然函数相对于 Z 给定数据 X 的当前条件分布和当前参数估计 theta 的条件期望；
2. 最大化步骤（M-step）：找到最大化该期望的参数 theta 的值。

可以使用贝叶斯定理在给定 X_i 和 theta 的情况下找到 Z_i 的条件分布：

现在定义完全对数似然的条件期望如下：

插入完整的对数似然函数并重新排列：

这样就完成了 E-step。在 M-step中，我们根据参数 theta 最大化上面计算的函数：

在这个的示例中，可以通过分析找到参数（通过求导并将其设置为零）。这里就不演示整个过程，只是提供答案。

在下面的实现中将使用与论文中相同数据来检查是否获得了相同的结果。Python 代码如下：

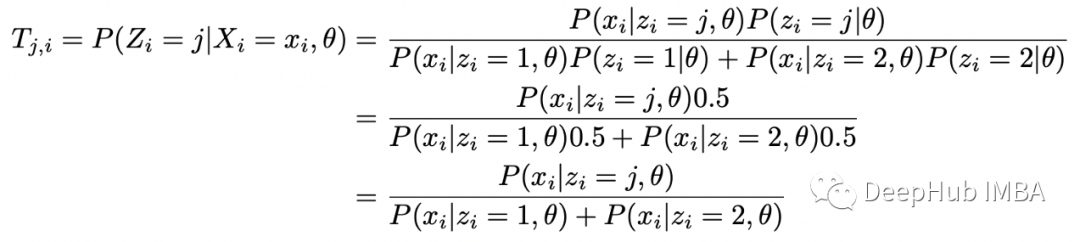
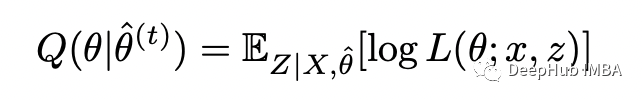
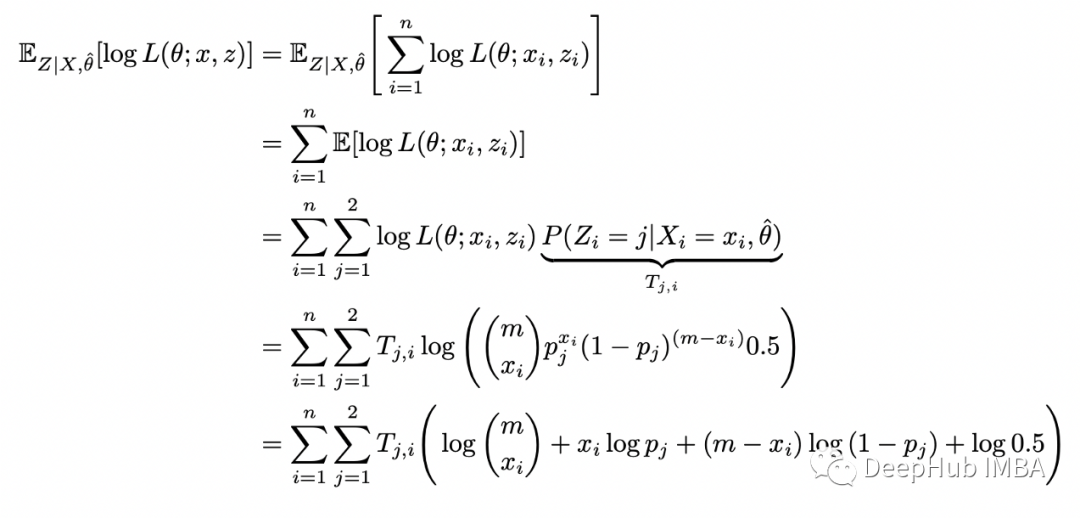
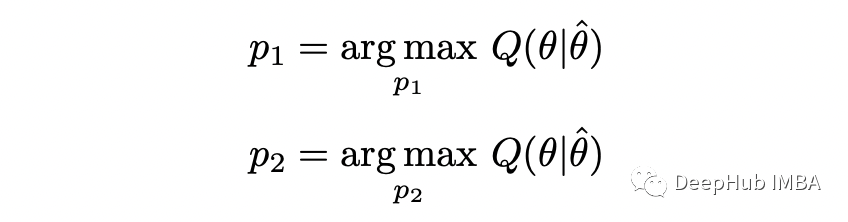
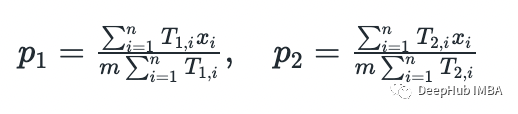
m = 10 # number of flips in each samplen = 5 # number of samplesxs = np.array([5,9,8,4,7])
theta = [0.6, 0.5] # initial guess p_1, p_2
for i in range(10):  p_1,p_2 = theta  T_1s = []  T_2s = []     # E-step  for x in xs:      T_1 = stats.binom(n=m,p=theta[0]).pmf(x) / (stats.binom(n=m,p=theta[0]).pmf(x) +                                                  stats.binom(n=m,p=theta[1]).pmf(x))      T_2 = stats.binom(n=m,p=theta[1]).pmf(x) / (stats.binom(n=m,p=theta[0]).pmf(x) +                                                  stats.binom(n=m,p=theta[1]).pmf(x))             T_1s.append(T_1)      T_2s.append(T_2)            # M-step  T_1s = np.array(T_1s)  T_2s = np.array(T_2s)  p_1 = np.dot(T_1s, xs) / (m * np.sum(T_1s))  p_2 = np.dot(T_2s, xs) / (m * np.sum(T_2s))  print(f'step:{i}, p1={p_1:.2f}, p2={p_2:.2f}')  theta = [p_1, p_2]

所有参数与论文中的完全相同。下面可以看到论文中的图表和上面代码的输出。

结果与论文中完全相同，这意味着 EM 算法的实现是正确的。

也可以使用数值求解器来最大化完全对数似然函数的条件期望，但在这种情况下使用解析解更容易。

现在让我们试着让问题变得更复杂一些。假设选择每个硬币的概率是未知的。那么我们将有两个二项式的混合，选择第一个硬币的概率为 tau，选择第二个硬币的概率为 1-tau。

我们重复与之前相同的步骤。定义完全似然函数：

在前面的例子中，给定 theta 的 Z 的条件概率是恒定的，现在它是带有参数 tau 的伯努利分布的 PMF。

计算完整的对数似然函数：

求给定 X 和 theta 的隐藏变量 Z 的条件分布：

计算对数似然的条件期望：

剩下的就是最大化关于参数 theta 的条件期望。上式中涉及概率 p_j 的项与之前的完全一样，所以 p_1 和 p_2 的解是相同的。最大化关于 tau 的条件期望，可以得到：

Python 中实现这个算法的代码如下

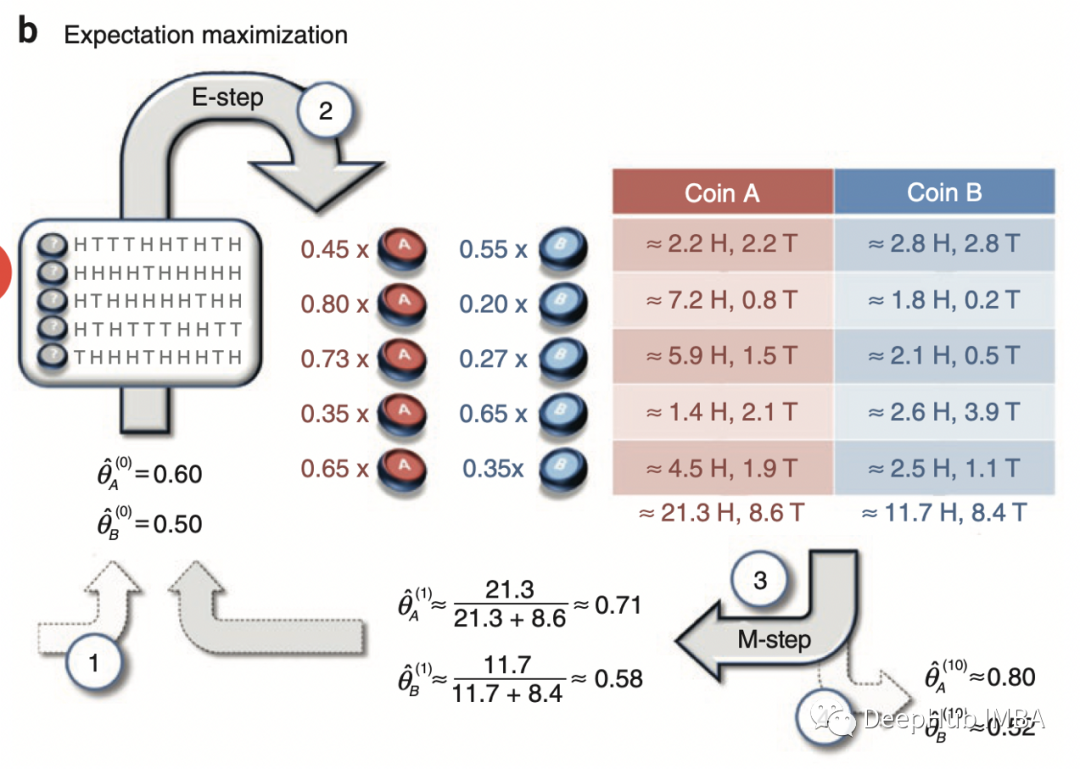
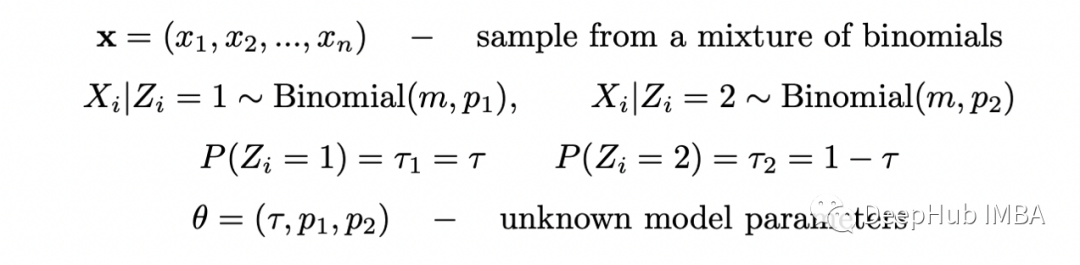
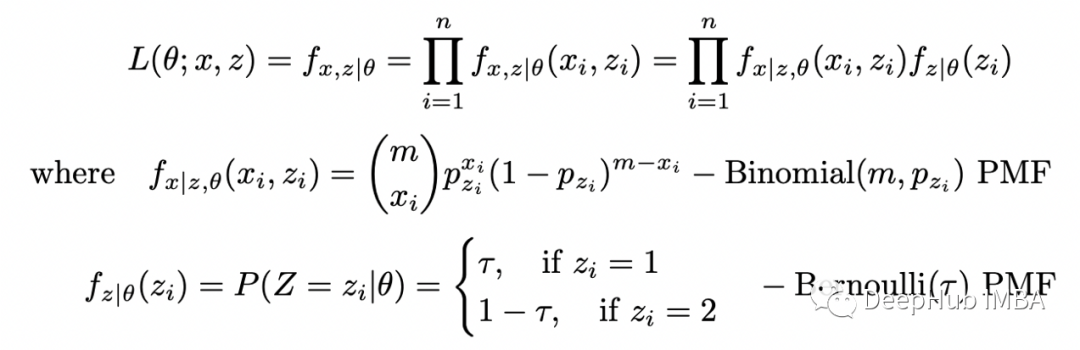
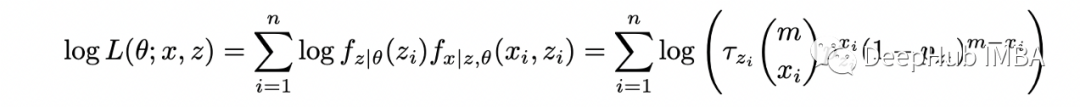
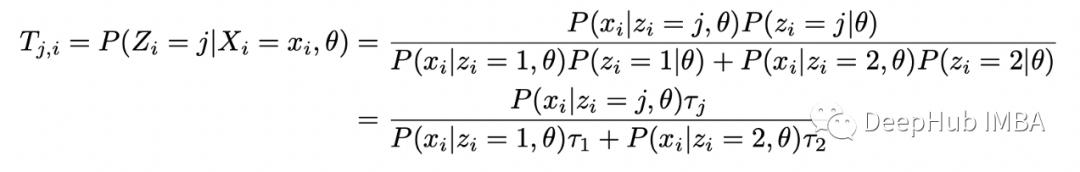
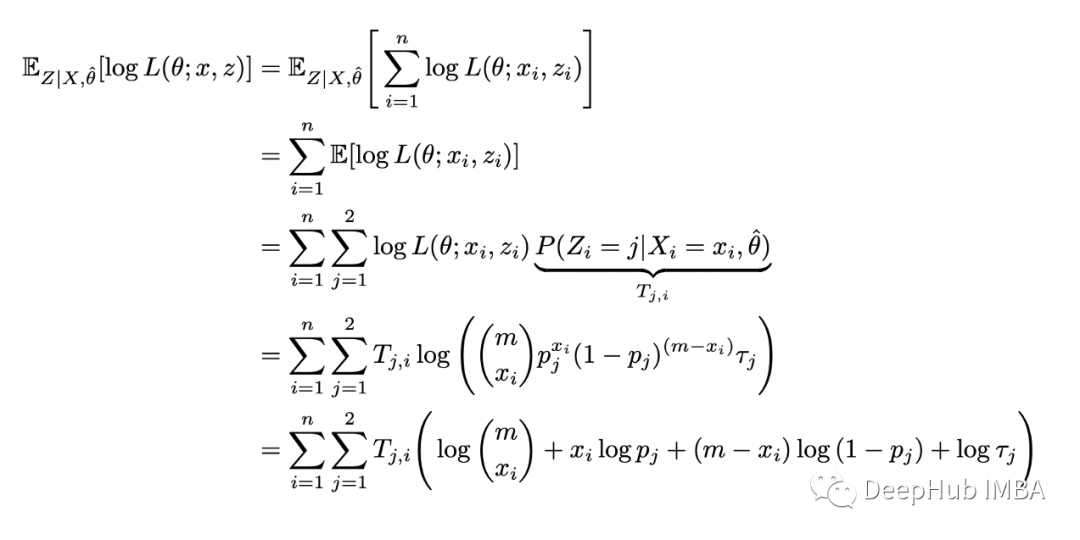
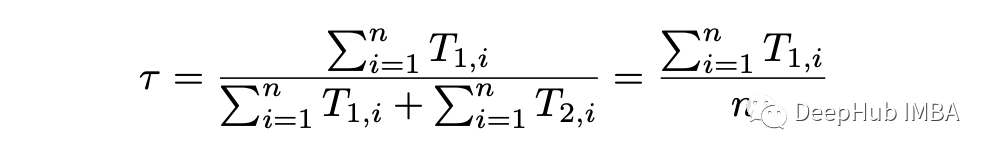
# model parametersp_1 = 0.1p_2 = 0.8tau_1 = 0.3tau_2 = 1-tau_1
m = 10 # number of flips in each samplen = 10 # number of samples
# generate datanp.random.seed(123)dists = [stats.binom(n=m, p=p_1), stats.binom(n=m, p=p_2)]xs = [dists[x].rvs() for x in np.random.choice([0,1], size=n, p=[tau_1,tau_2])]
# random initial guessnp.random.seed(123)theta = [np.random.rand() for _ in range(3)]
last_ll = 0max_iter = 100
for i in range(max_iter):  tau,p_1,p_2 = theta  T_1s = []  T_2s = []     # E-step  lls = []  for x in xs:      denom = (tau * stats.binom(n=m,p=p_1).pmf(x) + (1-tau) * stats.binom(n=m,p=p_2).pmf(x))      T_1 = tau * stats.binom(n=m,p=p_1).pmf(x) / denom      T_2 = (1-tau) * stats.binom(n=m,p=p_2).pmf(x) / denom      T_1s.append(T_1)      T_2s.append(T_2)      lls.append(T_1 * np.log(tau * stats.binom(n=m,p=p_1).pmf(x)) +                  T_2 * np.log(tau * stats.binom(n=m,p=p_2).pmf(x)))     # M-step  T_1s = np.array(T_1s)  T_2s = np.array(T_2s)  tau = np.sum(T_1s) / n  p_1 = np.dot(T_1s, xs) / (m * np.sum(T_1s))  p_2 = np.dot(T_2s, xs) / (m * np.sum(T_2s))  print(f'step:{i}, tau={tau}, p1={p_1:.2f}, p2={p_2:.2f}, log_likelihood={sum(lls):.2f}')  theta = [tau, p_1, p_2]     # stop when likelihood doesn't improve anymore  if abs(sum(lls) - last_ll) < 0.001:      break  else:      last_ll=sum(lls)

在前面的示例中，将算法运行了 10 次迭代，复制论文中的结果。但是在实践中，我们运行算法直到收敛，这意味着当对数似然停止改进时就停止算法。

算法的输出如上所示。由于问题的对称性，p_1 和 p_2 的概率被调换了但 结果仍然是正确的并且接近参数的真实值：我们有 p=0.85，概率为 0.8，p=0.1，概率为 0.2（真实值：p=0.8，概率为 0.7，p=0.1，概率为 0.3）。

本文的目的是通过一些简单的示例演示 EM 算法的基础知识。

本文的完整代码可以在这里找到：

https://github.com/financialnoob/misc/blob/305bf8bc7cbdddaf47d40078100ba27935ff4452/6.introduction_to_em_algorithm.ipynb

编辑：于腾凯
校对：林亦霖