算法与数据结构（五）哈希表

在讲哈希表之前，我们先来看看往一个数组插入数据的过程。

1.确认插入数据的下标；2.把数据放入数组。

拿日常生活中根据身高排队的例子来说，我们想获取到从低到高的姓名列表。我们就是在重复这样一个过程：

1.找到剩余队伍中身高最低人的姓名；2.放入当前数组元素的末尾；3.重复上过程。

但是这里有很大的限制，就是我们这种情况下能够知道一个姓名对应数组的下标是多少，很多其他情况下是无法知道的。在这种情况下使用数组处理这个场景是足够的。

然后看看这样一个场景，我们需要存储一个人的姓名及其对应的身高。这个时候我们用数组会怎么做？我们可以把数组存储的元素改成是 (姓名, 身高)，然后我们查找一个人的身高时，遍历数组找到姓名，然后返回身高。这种做法问题是查找时间复杂度过高，每次查找有 O(n) 的复杂度。我们能不能在 O(1) 的时间复杂度中查找到元素呢？

这时候就需要哈希表 HashTable。

什么是哈希表

哈希表 HashTable，也叫散列表、映射、字典等等，哈希表存储的是键值对 —— key、value。

也就是说，哈希表可以直接存储 "name": height 来解决上述问题。

哈希表关键点有三个：

•哈希函数•哈希冲突•装载因子

哈希函数

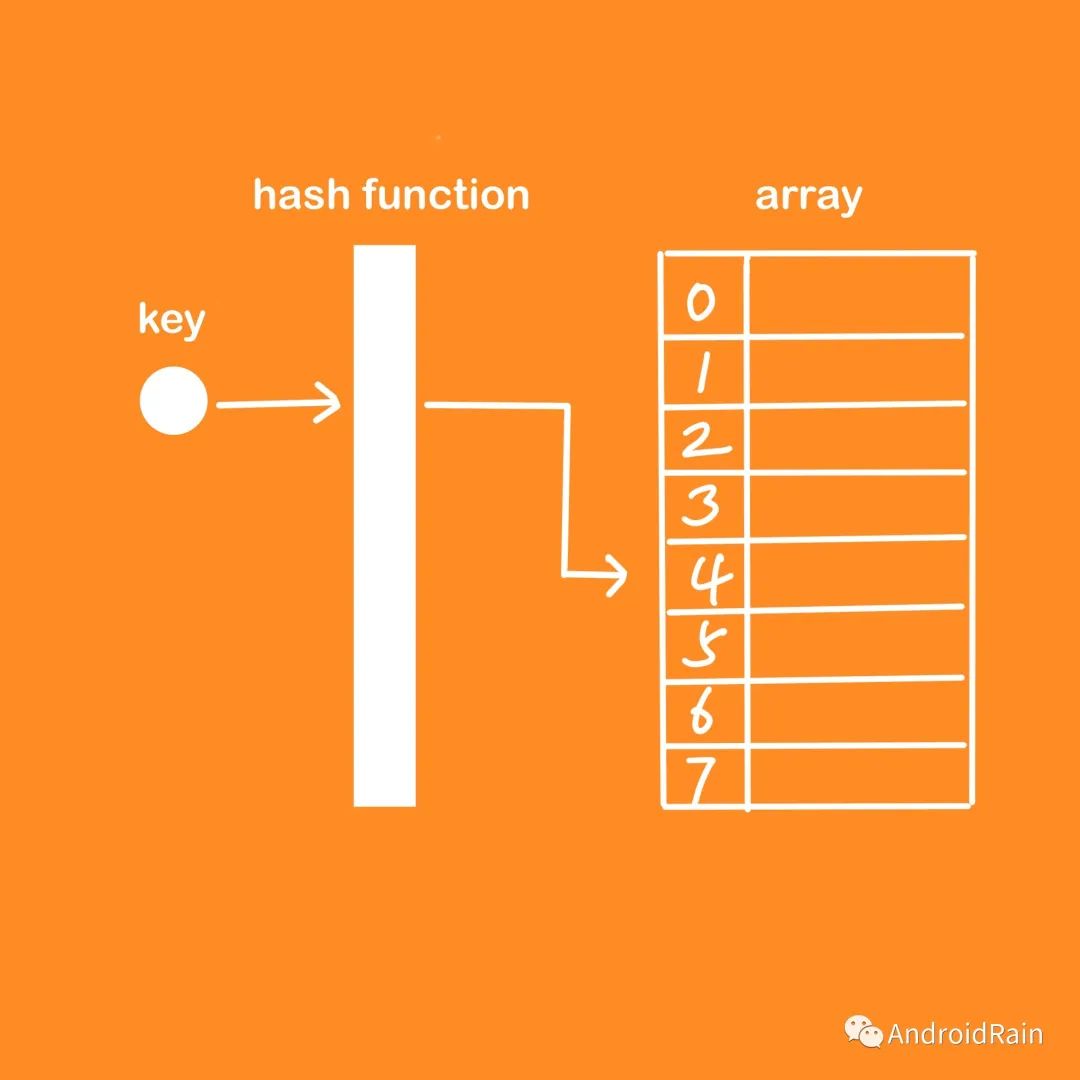
接下来我们结合上图解释一下哈希函数。

我们现在要往哈希表中放入 ("xiaoming", 175) 这组数据。发生了什么事情呢？

首先，数据的 key = "xiaoming" 会经过哈希表的哈希函数，转换成数组的下标 i。然后，我们把 value = 175 存储到 array[i] 的位置。

这里的哈希函数要满足几个特性：

1.相同的 key 经过哈希函数之后的输出一致；2.不同的 key 经过哈希函数之后的输出不同；3.哈希函数产生的输出在数组的有效范围内。

当我们在哈希表中查询 "xiaoming" 的身高时，哈希函数先计算该 key 对应的数组下标，然后取出数组中的数据。

这里我们可以看到，哈希表 = 哈希函数 + 数组，哈希表其实是数组的一种扩充，是由数组演化而来的，解决数组所无法解决的问题。这里我们也再强调一下，没有一种最优的数据结构和算法，只有更加适合某种场景、解决某种问题的数据结构和算法。

后续我们可以看到，哈希表也可能是另外一种形式：哈希表 = 哈希函数 + 数组 + 链表。

哈希冲突

你可能会想到，在我们存储过程中，虽然我们能够通过哈希函数得到一个 key 的整数值，但是我们的数组是有限的，假设这里的整数值为 k，数组长度为 n。我们通过 k % n 取余操作拿到 k 实际的数组下标。我们就会碰到两个整数对 n 取余之后的下标是相等的情况。比如 3 % 2 == 5 % 2 的情况。这个时候如果数组这个位置已经放置了元素，我们该怎么处理呢？

因为是哈希函数输出的值产生了冲突，所以这种情况我们称之为哈希冲突或者哈希值冲突。

而对应的解决办法有两种：

1.开放寻址法2.链表法

开放寻址法

开放寻址法中有线性探测法，该方法是说在发生冲突时，我们就依次在数组中往后查找，直到找到一个空闲位置。但是这种方法，在我们插入数据越来越多时，发生冲突的可能性就越来越大，线性探测时间也就越来越长。这时哈希表的插入、查找时间复杂度会退化，最差情况是 O(n)。Java 中的 ThreadLocalMap 使用此方法来解决哈希冲突。

当我们采用线性探测法时，如何对以上问题做出优化呢？

此时我们就要引入装填因子的概念，装填因子 = 已有元素个数 / 散列表的总长度。首先我们确定一个装填因子，然后当目前的因子大于我们设定的装填因子时，我们就对数组进行扩容，以此来保证有一定的剩余空间，进而减少线性探测时的时间复杂度。装填因子的设置也需要根据情况来看，要对线性探测的执行效率和扩容的成本上进行平衡。本质上还是时间、空间的平衡，当我们要求哈希表执行效率更高时，我们就可以设置更小的装填因子，增大剩余的数组空间，有利我们更快的进行线性探测；当我们内存比较紧张时，就需要设定更大的装填因子。

还有一种开放寻址法是双重散列。当一个哈希函数输出的下标值发生冲突时，采用另外一种哈希函数来重新计算下标值，直到找到空闲的位置。

链表法

链表法另辟蹊径，它把数组存储的元素改为链表，当发生冲突时不再尝试把数据存入到数组中，而是存储到同一下标的链表之中。上图展示了链表法的哈希表结构。这时我们发现 哈希表 = 哈希函数 + 数组 + 链表。Java 中的 LinkedHashMap 使用了链表法解决冲突问题。

当我们插入数据时，相当于在链表中插入元素的时间复杂度 O(1)。当我们查询时，取决于对应链表的长度 m，时间复杂度为 O(m)。

但是对于黑客来说，这种方法存在一个致命漏洞。黑客可以不断的往哈希表中放入 key 对应下标相同的数据，这会导致数组中只有该位置有长长的链表，进而导致查询时间十分漫长，对你的程序产生攻击的效果。我们称之为哈希表碰撞攻击。

所以一个能够产生均匀下标值的哈希函数十分重要。除了采用更优的哈希函数，我们还可以对链表做优化，比如说改造成红黑树解决查找过慢的问题。其实 Java 8 中就做了这个优化。

经过以上分析，我们知道开放寻址法更加适合数据量比较小、装填因子较小的场景，这也是 Java 中 ThreadLocalMap 使用开放寻址法的原因；链表法比较适合存储数据量比较大、对象比较大的情况。

什么是好的哈希表

结合上述内容，我们知道一个好的哈希表要有以下特性：

•快速的查询、插入、删除•性能稳定，不能够退化的太严重•内存占用合理

要保证以上特性，需要做到：

•哈希函数的输出比较均匀•合适的装填因子大小，高性能的动态扩容•合适的哈希冲突解决方法

总结

我们除了要了解哈希表是存储键值对的数据结构之外，还要掌握插入、删除、搜索一个数据的发生过程是怎样的。另外我们也要掌握哈希表的三个关键要素：哈希函数、冲突解决方法、装填因子。最后，我们要根据自己的实际场景，通过调整确定三个关键要素，选择合适的哈希表或者实现自己的哈希表。

实践

最后，推荐大家做一下 Leetcode 上的题目。可以先用自己的思路写一下代码，然后结合使用哈希表的方式再写一份代码。最后比较这两者的时间空间复杂度。

•有效的字母异位词^[1]•两数之和^[2]•三数之和^[3]

References

[1] 有效的字母异位词: https://leetcode-cn.com/problems/valid-anagram/
[2] 两数之和: https://leetcode-cn.com/problems/two-sum/
[3] 三数之和: https://leetcode-cn.com/problems/3sum/