用简单的代码,看懂 CPU 背后的重要机制
今天,stackoverflow 突然给我推送来一个问题。
我一看这个问题,竟然是 2012 年,也就是 8 年前的老问题。而其中的高票答案,都已经有 30000 多个赞了。
仔细一看,这个问题还真挺有意思。
这个问题针对如下这样一个简单的代码:

相信大家都能看懂。这段代码对 data 数组中所有大于等于 128 的值进行求和。这样的求和操作运行了 10 万轮。
下面,我们来看一下这段代码的性能。我们这样随机生成一个数组:
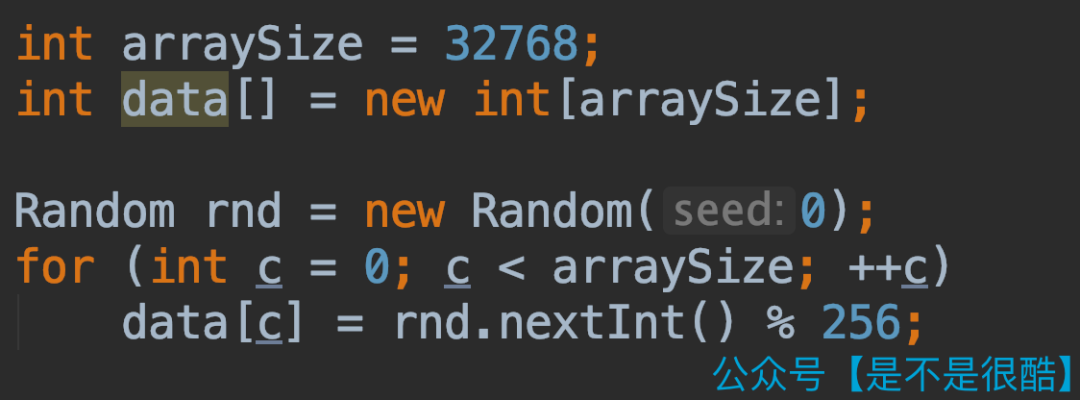
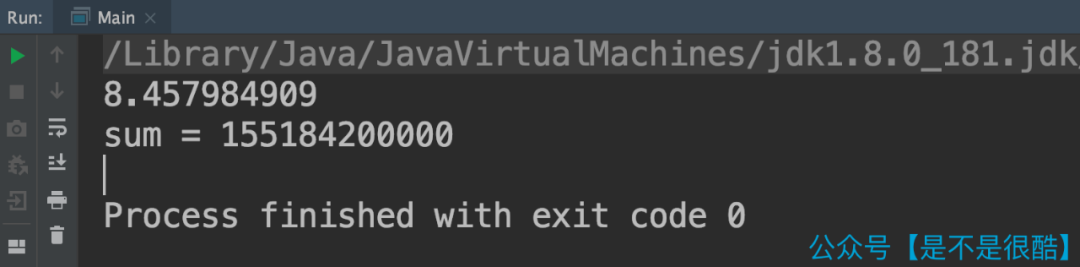
使用这个随机生成的数组,测试上面的代码。在我的计算机上,整体耗时是 8.5 秒左右。
下面问题来了。如果,我对这个随机的数组进行一遍排序。对排序后的数组执行上面的代码,性能会有怎样的影响?
可能很多同学都会认为,性能是差不多的。
这是因为,上面的代码过程,只是从头到尾扫描数组,对于数组中的每一个元素,判断其是否大于等于 128,如果是,就加入到 sum 中。
整个算法逻辑,和数组是否有序无关。有序的数组不会提前终止任何操作。不管是有序的数组,还是无序的数组,执行的操作数量是一样多的。
甚至,为了保持公平,我为随机数生成器添加了种子。所以,两次测试的数组中,大于等于 128 的元素个数都是一样的。这就意味着 sum += data[c]; 这个指令的执行次数是一致的。
区别只有:第二次执行,我先对数组进行了排序!
可是,实际结果却是这样的:
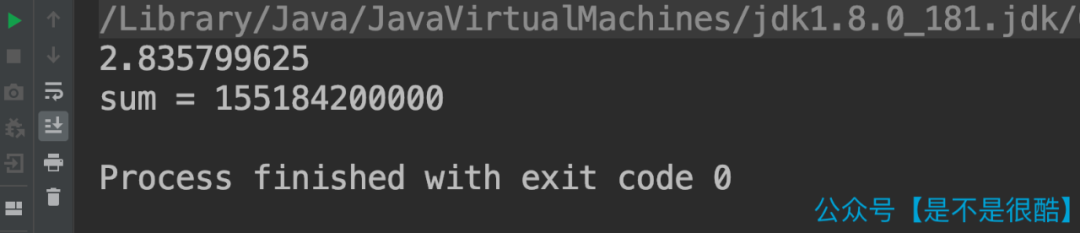
大家可以看到,由于测试数据是一样的,所以最终的 sum 结果是一样的。但是第二次,针对有序的数组做实验,消耗的时间仅仅是 2.8 秒左右,比无序的情况快了有 3 倍之多!
大家可能会觉得,这是不是 JVM 在搞什么鬼?那么,同样的代码逻辑,我们尝试用 C++ 实验一遍!

这段代码,我使用无序的数组测试,在我的计算机上,运行时间大概是 18.8 秒左右。(Debug 模式)
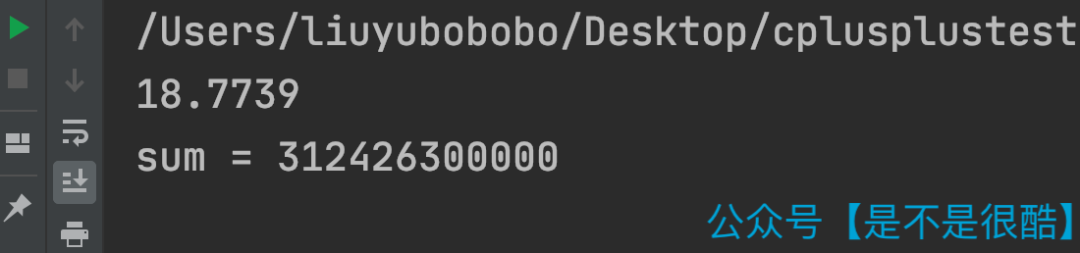
但是,当我将数组进行排序以后,运行时间则变成了 5.7 秒!(Debug 模式)
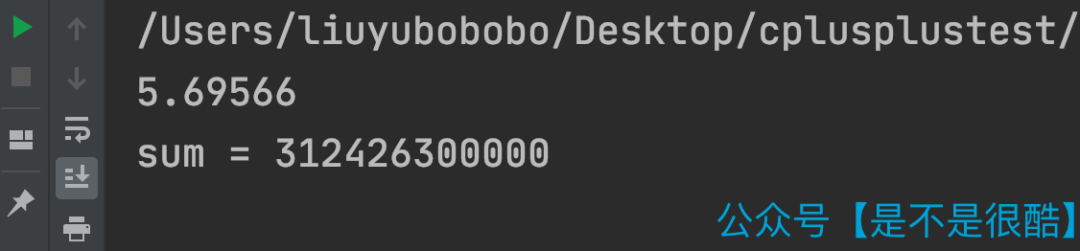
看来,这不是 JVM 的问题,而是有更加底层的优化机制在起作用。
这个机制,就是 CPU 的分支预测(Branch prediction)。
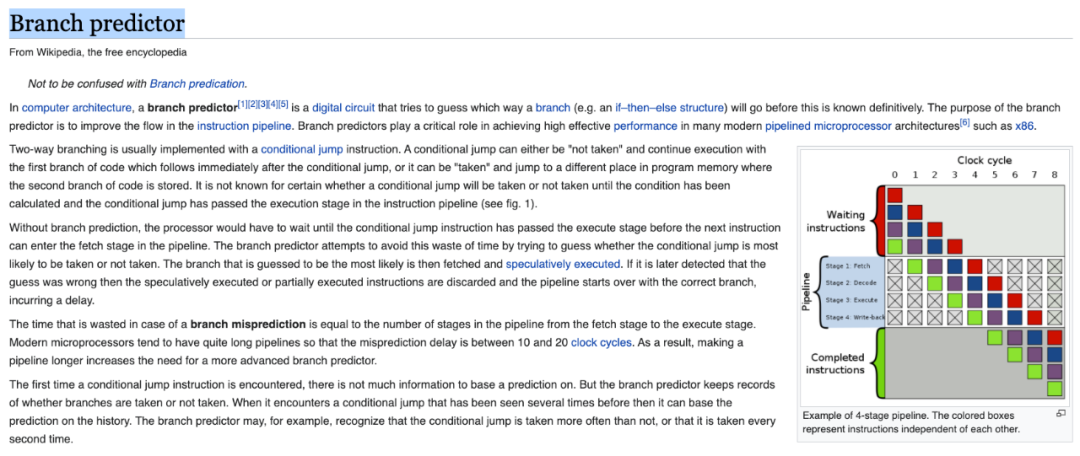
在具体讲解什么是 CPU 的分支预测之前,我们先来看一下什么是 CPU 指令执行的流水线(Pipeline)。
简单来说,一条指令的执行,在 CPU 内部,需要经过若干步骤。
比如,一个常见的模型,是 4 阶段流水线。即一条指令在 CPU 内部的执行,需要有 4 步:
fetch(获取指令) decode(解码指令) execute(执行指令) write-back(写回数据)
经过这四个阶段,才叫完全执行完了一条指令。
我们可以类比这样的一个例子。

我们去很多旅游景区吃饭,餐厅会使用半自助的形式由游客来选餐。游客进入选餐队伍之后,需要完成以下的事情,才能真正的执行完“买饭”这件事情,开始享用香喷喷的午餐:
选择一个主菜 选择一个配菜 选择一个饮料 去结账!
对于这个流程的执行,我们当然可以等 A 同学选好他的午饭:主菜,配菜和饮料,并且结完账,然后 B 同学再去选择他的午饭。▼

相信同学们都明白,这样做是低效的。
在 A 同学选择完主菜,去选择配菜的时候,B 同学就已经可以上去选择他的主菜了。▼

当 A 同学开始选择饮料的时候,B 同学已经可以选择配菜了,而 C 同学,此时就可以开始选择主菜了。▼

这样做,当 A 同学结完账的时候,E 同学都已经开始选主菜了。▼

很显然,这样做效率更高。
这就叫流水线。一个同学不需要等前一个同学完成所有选餐的步骤再去选餐,而只要完成一步,下一个同学就可以跟进。
CPU 的流水线完全同理。因为执行每一条指令需要 4 步。所以,在执行 A 指令的时候,一旦完成了 A 指令的 fetch 操作,进入 A 指令的 decode 阶段,就可以对下一条 B 指令执行 fetch 操作了。▼

当 A 指令 decode 完成,进入 execute 阶段,就可以开始对 B 指令进行 decode 了,同时,B 指令的下一条 C 指令,就可以开始 fetch 了。▼

那么问题来了,现在,如果一条指令是 if,怎么办?
为什么 if 指令会出问题?因为对于 if 指令,我们必须等它运行完,才能知道下一条指令是什么!下一条指令是根据 if 表达式中的结果是真还是假来决定的!

而实际情况,可能不是简单的一条指令的问题。因为 if 表达式的计算,可能涉及多个操作。
比如上面代码中,就算是 if(data[c] >= 128) 这个简单的逻辑,我们也需要先解析出 c 的值,再拿出 data,再从 data 中拿出 c 这个索引对应的元素,再去比较这个元素是不是大于等于 128。
可以想象,后面的指令就停在这里了。需要等这一系列 if 判断相关的指令都执行完,计算出最终结果,才能决定下面把哪条指令放入流水线。
这显然会对性能产生影响。于是,现代 CPU 对于这种情况,都设计了一个机制,叫做分支预测(Branch Prediction)。
简单来说,分支预测就是针对这种 if 指令,不等它执行完毕,先预测一下执行的结果可能是 true 还是 false,然后将对应条件的指令放进流水线。

如果等 if 语句执行完毕,发现最初预测错了,那么我们把这些错误的指令计算结果扔掉就好了,转而重新把正确的指令放到流水线中执行。
这种情况,虽然也会损失一些性能,但可以接受。因为反正如果不做预测,时间也会空耗,对应就是 CPU 的时钟周期空转。
但一旦预测对了,那就是一个巨大的性能提升。因为后续指令已经进入流水线,执行起来了。我们直接继续这个过程就好。
这就是 CPU 的分支预测,是不是很简单?
具体 CPU 的分支预测是如何实现的?不同的体系架构,包括同一体系架构 CPU 的不同版本,会有不同的策略。
但是,整体上,一个重要的策略,是参考某条 if 指令执行过程中判断为 true 或者 false 的历史记录。
这应用了在计算机领域经常使用的一个原理:局部性原理。
通常在操作系统课程中,都会介绍这个重要的原理。很多算法或者数据结构的设计,也是基于这个原理的。
比如,计算机体系结构设计,都是分层的。从外存;到内存;到一级缓存,二级缓存;到寄存器。存储容量逐渐减小;但是,运算速度越来越快。
操作系统在运行的过程中,就需要做一个重要的调度:决定把什么数据放到更高层次的缓存中,以提升程序运行的效率。
局部性原理说的就是:
如果一个信息正在访问,那么近期很有可能会再次访问,这叫时间局部性;
如果一个信息正在访问,那么近期访问的其他信息,大概率在空间地址上,和这个信息的空间地址邻近,这叫空间局部性。
这样的局部性原理同样被应用在了 CPU 对 if 的条件分支预测上。一个 if 现在被判为 true,下次,会更高概率的判为 true。当然,实际的预测逻辑会更复杂,但是,局部性原理是一个重要的参考。
我称之为:if 局部性原理。
(我瞎编的,听说多使用这种让人摸不到头脑的术语,会显得文章更加高大上。)

现在,大家应该明白了。对于文章开始讨论的代码,如果数据经过了排序,那么,所有小于 128 的数据就都在数组的前面;所有大于等于 128 的数据,就都在数组的后面。
那么,在下面的执行过程中,CPU 根据历史记录对 if 进行分支预测,就会高概率命中,提升性能。
而对于完全随机的数组,数据是否大于等于 128 是完全随机的,这就导致 CPU 的分支预测总是失效,从而,降低了性能。
好了,原理解释清楚了。下面,我们看一下,在这个程序中,我们可不可以避免这种分支预测经常失败导致的性能问题?
答案是,可以!我们需要想办法去掉 if 判断。
怎么去除?在这个程序中,我们可以使用这样的方式:
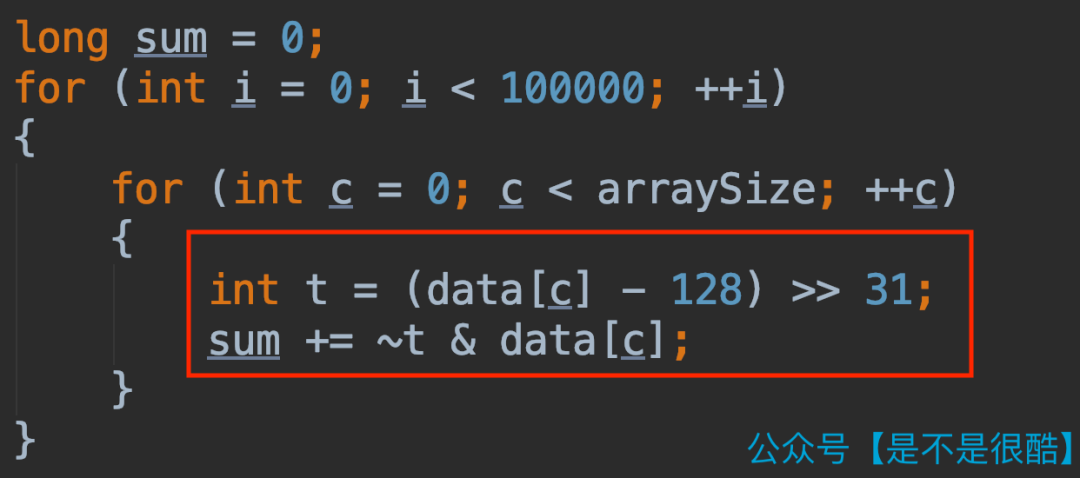
注意上面的代码中,红框的部分,代替了原来的 if 逻辑。
为什么这是等价的?我们可以简单分析一下。
首先看变量 t 的值。他是 data[c] - 128 的结果右移 31 位。
大家可以想象:
如果 data[c] - 128 是非负数,右移补零,符号位也是 0。右移 31 位的结果是 0x0000;
如果 data[c] - 128 是负数,右移补一,符号位也是 1。右移 31 位的结果,是 0xffff。
在下面的 sum 计算中,先对 t 取反。
那么如果 data[c] - 128 是非负数,即 data[c] >= 128,t 就是 0x0000,取反的结果是 0xffff。0xffff 每一位都是 1,和 data[c] 做与运算,结果还是 data[c] 自身。此时,相当于把 data[c] 加入了 sum 中。
如果 data[c] - 128 是负数,即 data[c] < 128,t 就是 0xffff。此时对 t 取反,结果为 0。0 和 data[c] 做与运算,结果还是 0。此时,相当于 sum 什么都没有加。
所以,这和判断一下 data[c] 是否大于等于 128,如果大于等于,再做加法运算,是等价的。但是,我们去掉了 if 判断。
这个代码的性能是怎样的?在我的计算机上,不做排序的话,只需要 1.7 秒(对比之前的 8.4 秒)。

更重要的是,这个代码的性能,不再受原始数组是否排序而影响。当排序以后,执行时间,也是同一个数量级的。

使用 C++ 测试,结果是类似的。
怎么样,是不是很酷?
关于分支预测,有兴趣的同学,可以参考维基百科的 Branch predictor 词条,了解更多。
完
帅地搞了个小号,我会在这个公众号分享读者问过我的问题,并且给予最真实的回答,同时也会分享自己学习方法、挣钱经历、工作经历、个人经历、沙雕日常,我相信,我的经历与想法,一定可以给你带来一些帮助!扫一扫进入帅地的私密沙雕小号
