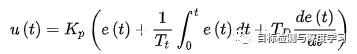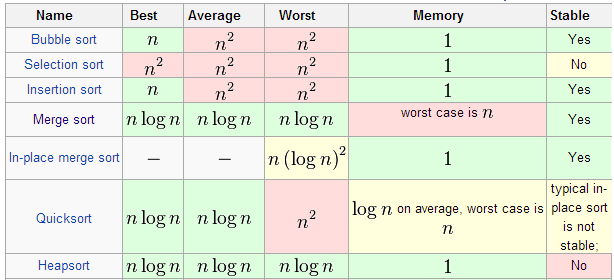文章基于《统治世界的十大算法》进行了系统性的整理,其作者George Dvorsky试图解释算法之于当今世界的重要性,以及哪些算法对人类文明做出过巨大的贡献。
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。
冒泡排序(bubble sort) — O(n^2)
鸡尾酒排序(Cocktail sort,双向的冒泡排序) — O(n^2)
插入排序(insertion sort)— O(n^2)
桶排序(bucket sort)— O(n); 需要 O(k) 额外空间
计数排序(counting sort) — O(n+k); 需要 O(n+k) 额外空间
合并排序(merge sort)— O(nlog n);需要 O(n) 额外空间
原地合并排序— O(n^2)
二叉排序树排序 (Binary tree sort) — O(nlog n)期望时间;O(n^2)最坏时间;需要 O(n) 额外空间
鸽巢排序(Pigeonhole sort)— O(n+k); 需要 O(k) 额外空间
基数排序(radix sort)— O(n·k); 需要 O(n) 额外空间
Gnome 排序— O(n^2)
图书馆排序— O(nlog n) withhigh probability,需要(1+ε)n额外空间
选择排序(selection sort)— O(n^2)
希尔排序(shell sort)— O(nlog n) 如果使用最佳的现在版本
组合排序— O(nlog n)
堆排序(heapsort)— O(nlog n)
平滑排序— O(nlog n)
快速排序(quicksort)— O(nlog n) 期望时间,O(n^2) 最坏情况;对于大的、乱数列表一般相信是最快的已知排序
Introsort—O(nlog n)
Patience sorting— O(nlog n+k) 最坏情况时间,需要额外的 O(n+ k) 空间,也需要找到最长的递增子串行(longest increasing subsequence)
Bogo排序— O(n× n!) 期望时间,无穷的最坏情况。
Stupid sort— O(n^3); 递归版本需要 O(n^2)额外存储器
珠排序(Bead sort) — O(n) or O(√n),但需要特别的硬件
Pancake sorting— O(n),但需要特别的硬件
stooge sort——O(n^2.7)很漂亮但是很耗时
傅立叶变换:表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。傅立叶是一位法国数学家和物理学家,原名是JeanBaptiste Joseph Fourier(1768-1830), Fourier于1807年在法国科学学会上发表了一篇论文,论文里描述运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号都可以由一组适当的正弦曲线组合而成。当时审查这个论文拉格朗日坚决反对此论文的发表,而后在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。直到拉格朗日死后15年这个论文才被发表出来。谁是对的呢?拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅立叶是对的。为什么我们要用正弦曲线来代替原来的曲线呢?如我们也还可以用方波或三角波来代替呀,分解信号的方法是无穷多的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正余弦曲线信号输入后,输出的仍是正余弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正余弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。

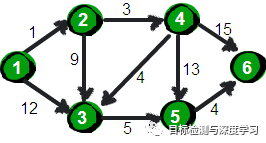


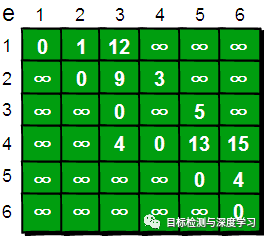


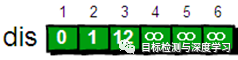
下面我们来模拟一下:

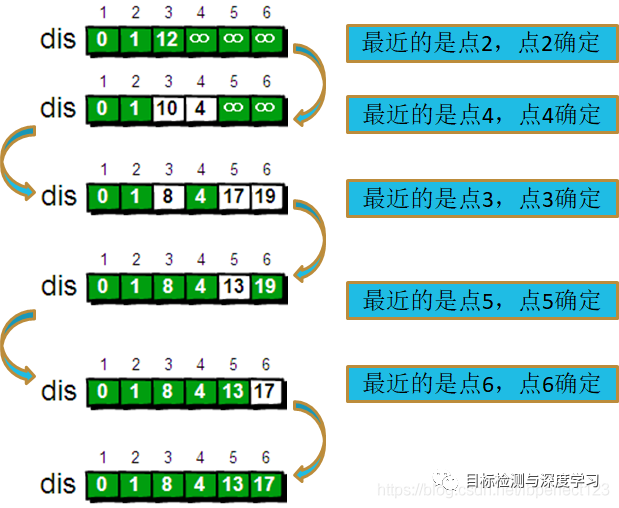
这就是Dijkstra算法的基本思路。
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击,已被ISO推荐为公钥数据加密标准。
一、公钥加密算法是什么?
公钥加密,非对称加密。简单的说,就是明文通过公钥加密,但只能通过密钥来解密。假设机器A需要向机器B传送一段极隐私的数据,要求只有机器B能解密,就需要机器B生成一对密钥,其中公钥向包括机器A在内的所有人公布,那机器A就可以用公钥加密传送的数据,机器B接收到之后用私钥解密,其他人没有私钥,即使捕获到机器A发送的消息,也无法解密。
二、 RSA实现基本思路
RSA公钥密码体制描述如下:(m为明文,c为密文)
1. 选取两个大素数p,q。p和q保密
2. 计算n=pq,r=(p-1)(q-1)。n公开,r保密
3. 随机选取正整数1<e<r,满足gcd(e,r)=1.e是公开的加密密钥
4. 计算d,满足de=1(mod r).d是保密的解密密钥
5. 加密变换: c=m^e mod n
6. 解密变换: m=c^d mod n
三、 RSA为什么能用公钥加密,私钥解密?
RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
今天只有短的RSA钥匙才可能被强力方式解破。到2008年为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被解破的。但在分布式计算和量子计算机理论日趋成熟的今天,RSA加密安全性受到了挑战。
安全哈希(散列)算法(Secure Hash Algorithm,SHA)是一个密码散列函数家族,是FIPS所认证的安全散列算法。能计算出一个数字消息所对应到的,长度固定的字符串(又称消息摘要)的算法。且若输入的消息不同,它们对应到不同字符串的机率很高。SHA家族的五个算法,分别是SHA-1、SHA-224、SHA-256、SHA-384,和SHA-512,由美国国家安全局(NSA)所设计,并由美国国家标准与技术研究院(NIST)发布;是美国的政府标准。后四者有时并称为SHA-2。SHA-1在许多安全协定中广为使用,包括TLS和SSL、PGP、SSH、S/MIME和IPsec,曾被视为是MD5(更早之前被广为使用的杂凑函数)的后继者。但SHA-1的安全性如今被密码学家严重质疑;虽然至今尚未出现对SHA-2有效的攻击,它的算法跟SHA-1基本上仍然相似;因此有些人开始发展其他替代的杂凑算法。后台接口接受相关参数,然后将(A,B)在后台进行SHA1加密,获取加密摘要D,最后将D与C进行比较,如果C == D ,则A和B在传输过程中参数没有被窃取改变;如果C != D,则说明A和B已经在传输过程中发生了改变,最好不要使用。在APP与后端服务器接口调用的时候,将需要传输的参数进行关键参数(如:String A,String B)进行SHA1加密,获取加密之后的摘要(C);然后在接口调用的时候将参数原文(A,B)和加密的摘要(C)一起传输给后台服务器。
整数因式分解是在计算机领域被大量使用的数学算法,没有这个算法,信息加密会更不安全。该算法定义了一系列步骤,得到将一合数分解为更小因子的质数分解式。这被认为是一种FNP问题,它是NP分类问题的延伸,极其难以解决。许多加密协议(如RSA算法)都基于这样一个原理。相对于素数判定来说,因式分解的实现就没办法达到那么快速了。因子分解至今仍没有类似于素数判定的多项式算法,这也成为了RSA公钥系统安全得以保障的基础。如果一个算法能够快速地对任意整数进行因式分解,RSA的公钥加密体系就会失去其安全性。鉴于这两个问题的难度相差较大,在我们施行分解之前,最好是预先知道目标整数的确不是一个素数,否则很可能花费了很大力气只干了素数判定的活 ——杀鸡用牛刀了。因式分解的分为一般方法和特殊方法两大类,通常倾向于先针对数的特殊性,使用对应的特殊方法,如果目标数的形式不那么特殊,再尝试使用一般方法。当然,前者往往要比后者快上许多。
量子计算的诞生使我们能够更容易地解决这类问题,同时它也打开了一个全新的领域,使得我们能够利用量子世界中的特性来保证系统安全。
常见的链接分析算法除了鼎鼎有名的PageRank,还有HITS、SALSA、Hilltop以及主题PageRank等等。需要重点理解的是PageRank和HITS,后面这些算法都是以它们为基础的。
绝大部分链接分析算法建立在两个概念模型,它们是:
随机游走模型:
针对浏览网页用户行为建立的抽象概念模型,用户上网过程中会不断打开链接,在相互有链接指向的网页之间跳转,这是直接跳转,如果某个页面包含的所有链接用户都不感兴趣则可能会在浏览器中输入另外的网址,这是远程跳转。该模型就是对一个直接跳转和远程跳转两种用户浏览行为进行抽象的概念模型;典型的使用该模型的算法是PageRank;
子集传播模型:
基本思想是把互联网网页按照一定规则划分,分为两个甚至是多个子集合。其中某个子集合具有特殊性质,很多算法从这个具有特殊性质的子集合出发,给予子集合内网页初始权值,之后根据这个特殊子集合内网页和其他网页的链接关系,按照一定方式将权值传递到其他网页。典型的使用该模型的算法有HITS和Hilltop算法。
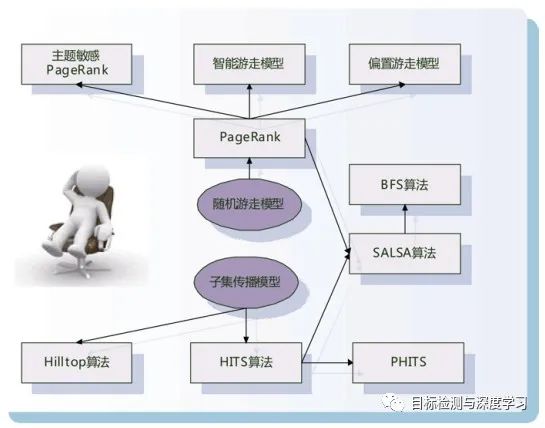
从图中可看出,在众多算法中,PageRank和HITS算法可以说是最重要的两个具有代表性的链接分析算法,后续的很多链接分析算法都是在这两个算法基础上衍生出来的改进算法。
你是否曾经用过飞机、汽车、卫星服务或手机网络?你是否曾经在工厂工作或是看见过机器人?如果回答是肯定的,那么你应该已经见识过这个算法了。大体上,这个算法使用一种控制回路反馈机制,将期望输出信号和实际输出信号之间的错误最小化。无论何处,只要你需要进行信号处理,或者你需要一套电子系统,用来自动化控制机械、液压或热力系统,这个算法都会有用武之地。PID即:Proportional(比例)、Integral(积分)、Differential(微分)的缩写。顾名思义,PID控制算法是结合比例、积分和微分三种环节于一体的控制算法,它是连续系统中技术最为成熟、应用最为广泛的一种控制算法,该控制算法出现于20世纪30至40年代,适用于对被控对象模型了解不清楚的场合。实际运行的经验和理论的分析都表明,运用这种控制规律对许多工业过程进行控制时,都能得到比较满意的效果。PID控制的实质就是根据输入的偏差值,按照比例、积分、微分的函数关系进行运算,运算结果用以控制输出。在工业过程中,连续控制系统的理想PID控制规律为: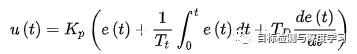
式中,Kp——比例增益,Kp与比例度成倒数关系;
Tt——积分时间常数;
TD——微分时间常数;
u(t)——PID控制器的输出信号;
e(t)——给定值r(t)与测量值之差。
可以这样说,如果没有这个算法,现代文明将不复存在。
在现今的电子信息技术领域,正发生着一场有长远影响的数字化革命。由于数字化的多媒体信息尤其是数字视频、音频信号的数据量特别庞大,如果不对其进行有效的压缩就难以得到实际的应用。因此,数据压缩算法已成为当今数字通信、广播、存储和多媒体娱乐中的一项关键的共性技术。用于多媒体数据的压缩方法众多,可按主要特点将它们分成不同的类型:1、无损压缩:能够无失真地从压缩后的数据重构,准确地还原原始数据。可用于对数据的准确性要求严格的场合,如可执行文件和普通文件的压缩、磁盘的压缩,也可用于多媒体数据的压缩。该方法的压缩比较小。如差分编码、RLE、Huffman编码、LZW编码、算术编码。2、有损压缩:有失真,不能完全准确地恢复原始数据,重构的数据只是原始数据的一个近似。可用于对数据的准确性要求不高的场合,如多媒体数据的压缩。该方法的压缩比较大。例如预测编码、音感编码、分形压缩、小波压缩、JPEG/MPEG。若编解码算法的复杂性和所需时间差不多,则为对称的编码方法,多数压缩算法都是对称的。但也有不对称的,一般是编码难而解码容易,如Huffman编码和分形编码。但用于密码学的编码方法则相反,是编码容易,而解码则非常难。在视频编码中会同时用到帧内与帧间的编码方法,帧内编码是指在一帧图像内独立完成的编码方法,同静态图像的编码,如JPEG;而帧间编码则需要参照前后帧才能进行编解码,并在编码过程中考虑对帧之间的时间冗余的压缩,如MPEG。在有些多媒体的应用场合,需要实时处理或传输数据(如现场的数字录音和录影、播放MP3/RM/VCD/DVD、视频/音频点播、网络现场直播、可视电话、视频会议),编解码一般要求延时≤50ms。这就需要简单/快速/高效的算法和高速/复杂的CPU/DSP芯片。有些压缩算法可以同时处理不同分辨率、不同传输速率、不同质量水平的多媒体数据,如JPEG2000、MPEG-2/4。
在统计学的不同技术中需要使用随机数,比如在从统计总体中抽取有代表性的样本的时候,或者在将实验动物分配到不同的试验组的过程中,或者在进行蒙特卡罗模拟法计算的时候等等。
随机数是专门的随机试验的结果。在统计学的不同技术中需要使用随机数,比如在从统计总体中抽取有代表性的样本的时候,或者在将实验动物分配到不同的试验组的过程中,或者在进行蒙特卡罗模拟法计算的时候等等。产生随机数有多种不同的方法。这些方法被称为随机数发生器。随机数最重要的特性是:它所产生的后面的那个数与前面的那个数毫无关系。双一流大学研究生团队创建,专注于目标检测与深度学习,希望可以将分享变成一种习惯!整理不易,点赞三连↓