数据结构与算法系列(三)—选择排序
点击蓝字关注我们
 数据结构与算法系列(三)—选择排序
数据结构与算法系列(三)—选择排序前言
大家好,牧码心今天给大家推荐一篇数据结构与算法系列(三)—选择排序的文章,希望对你有所帮助。大纲如下:
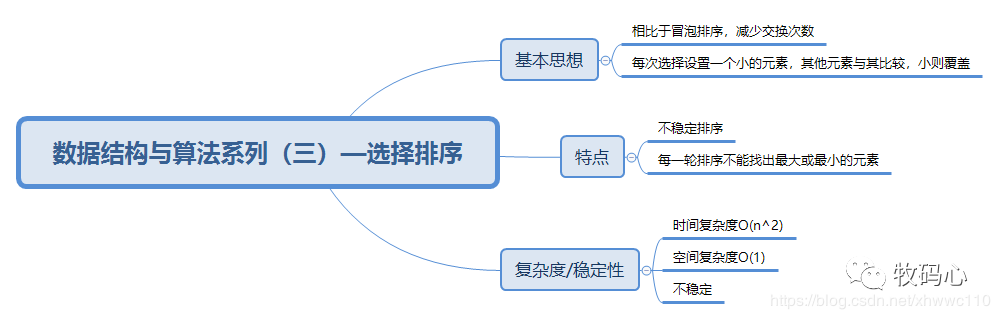
选择排序基本介绍
选择排序图文说明
选择排序时空复杂度和稳定性
选择排序具体实现
选择排序基本介绍
选择排序 是一种较简单的排序算法,排序过程类似于队伍排队,每次选出相对最高或最小的同学排列。相比于冒泡排序省去了每轮交换多次的开销。其基本思想是:首先在未排序的数列中找到最小(最大)元素,然后将其存放到数列的起始位置;接着,再从剩余未排序的元素中继续寻找最小(最大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序图文说明
下面以数列{20,40,30,10,60,50}为例,演示选择排序过程
 选择排序过程
选择排序过程
排序流程说明:第1趟:i=0.找出a[1…5]中的最小值a[3]=10,然后将a[0]和a[3]互换。数列变化:
20,40,30,10,60,50->10,40,30,20,60,50
第2趟:i=1.找出a[2…5]中的最小值a[3]=20,然后将a[1]和a[3]互换。数列变化:
10,40,30,20,60,50->10,20,30,40,60,50
第3趟:i=2.找出a[3…5]中的最小值,由于该最小值大于a[2],该趟不做任何处理。
第4趟:i=3.找出a[4…5]中的最小值,由于该最小值大于a[3],该趟不做任何处理。
第5趟:i=4.交换a[4]和a[5]的数据,数列变化:
10,20,30,40,60,50->10,20,30,40,50,60
选择排序时空复杂度和稳定性
| 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|
| O(n^2) | O(1) | 不稳定 |
说明
时间复杂度:选择排序每一轮需要选出最小值min,在交互到最左边的时间复杂度为O(n),共需要进行n-1轮。所以总的时间复杂度为O(n^2) ;
空间复杂度 :选择排序是原地排序,没有产生额外的空间,则为O(1) ;
稳定性 :选择排序是不稳定的,比如被排序的序列存在多个相同的的元素时,该排序会打乱各元素原有的相对顺序。
选择排序实现
选择排序(java版)
1/*
2 * @Author:greekw
3 * @Desc: 选择排序,类比站队
4 * @Date 0:04 2020/7/22
5 * @Param [array]
6 * @return void
7 **/
8 public static void selectSort(int[] array){
9 for (int i = 0; i < array.length ; i++) {
10 // 设置初始的最小位置
11 int minIndex = i;
12
13 // 找出最小元素的位置
14 for (int j = i; j < array.length; j++) {
15
16 minIndex = (array[j] < array[minIndex]) ? j : minIndex;
17 }
18
19 // 交换元素,排序
20 int temp = array[i];
21 array[i] = array[minIndex];
22 array[minIndex] = temp;
23 }
24 }
25 // 测试用例
26 public static void main(String[] args) {
27 int[] selectArray= new int[]{20,40,30,10,60,50};
28 selectSort(selectArray);
29 System.out.println(Arrays.toString(selectArray));
30 }
往期回顾
THE
END
长按二维码关注,一起学习、思考、成长
扫码关注我们
微信号 : lx_three
