三道【只出现一次的数】一文轻松搞定！

今天我们来做几道非常经典的题目，第一道题目我们会用多种方法解答，虽然这是一道简单题目，但是我们学会了这几种解题方法，完全可以轻松应对后面两道中等题目。废话不多说，我们来看题目吧。

为保证严谨性，文章中的所有代码均经过测试，大家可以放心食用

题目来源：leetcode 136只出现一次的数(简单)，137只出现一次的数Ⅱ(中等)260只出现一次的数Ⅲ(中等)

只出现一次的数

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

示例 1:

输入: [2,2,1] 输出: 1

示例 2:

输入: [4,1,2,1,2] 输出: 4

这个题目非常容易理解，就是让我们找出那个只出现一次的数字，那么下面我们来看一下这几种解题方法吧

HashMap

用 HashMap 的这个方法是很容易实现的，题目要求不是让我们求次数嘛，那我们直接遍历数组将每个数字和其出现的次数存到哈希表里就可以了，然后我们再从哈希表里找出出现一次的那个数返回即可。

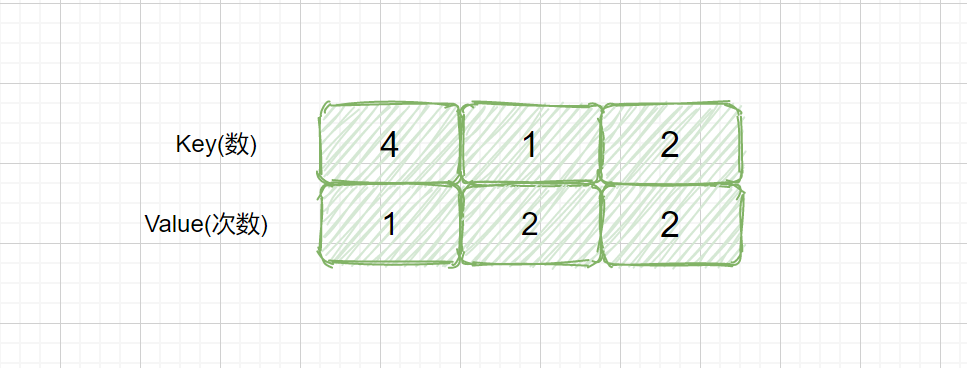
题目代码

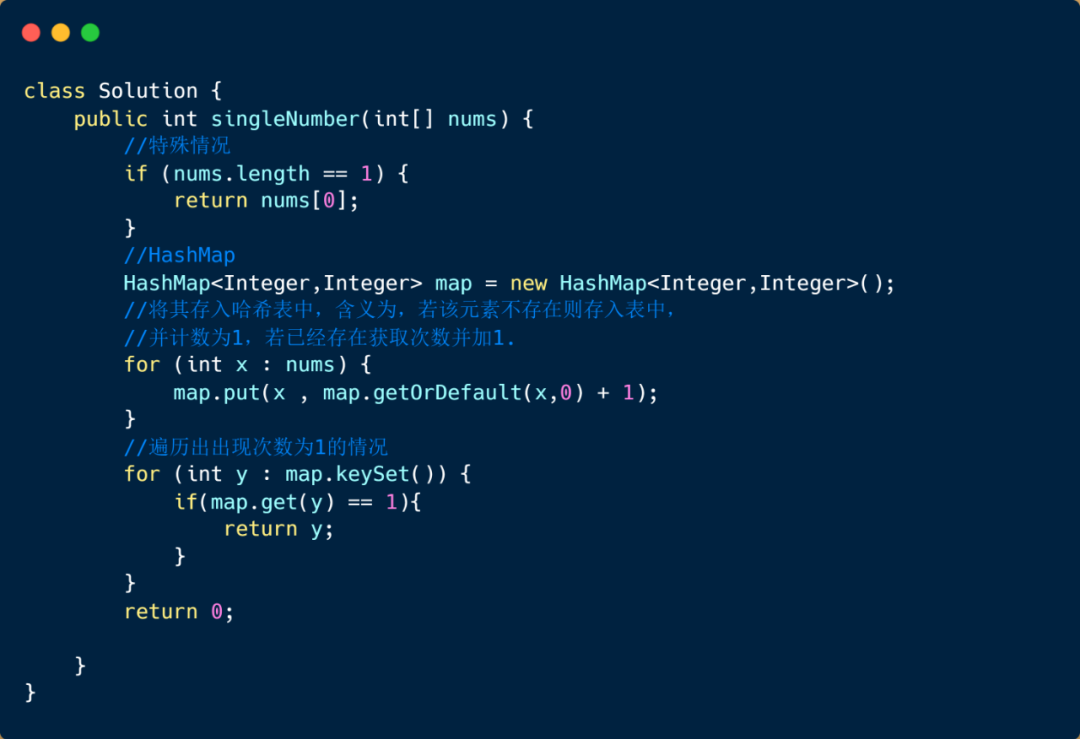
排序搜索法

这个方法也是特别容易想到的，我们首先对数组进行排序，然后遍历数组，因为数组中其他数字都出现两次，只有目标值出现一次，所以则让我们的指针每次跳两步，当发现当前值和前一位不一样的情况时，返回前一位即可，当然我们需要考虑这种情况，当我们的目标值出现在数组最后一位的情况，所以当数组遍历结束后没有返回值，则我们需要返回数组最后一位，下面我们看一下动图解析。

题目代码

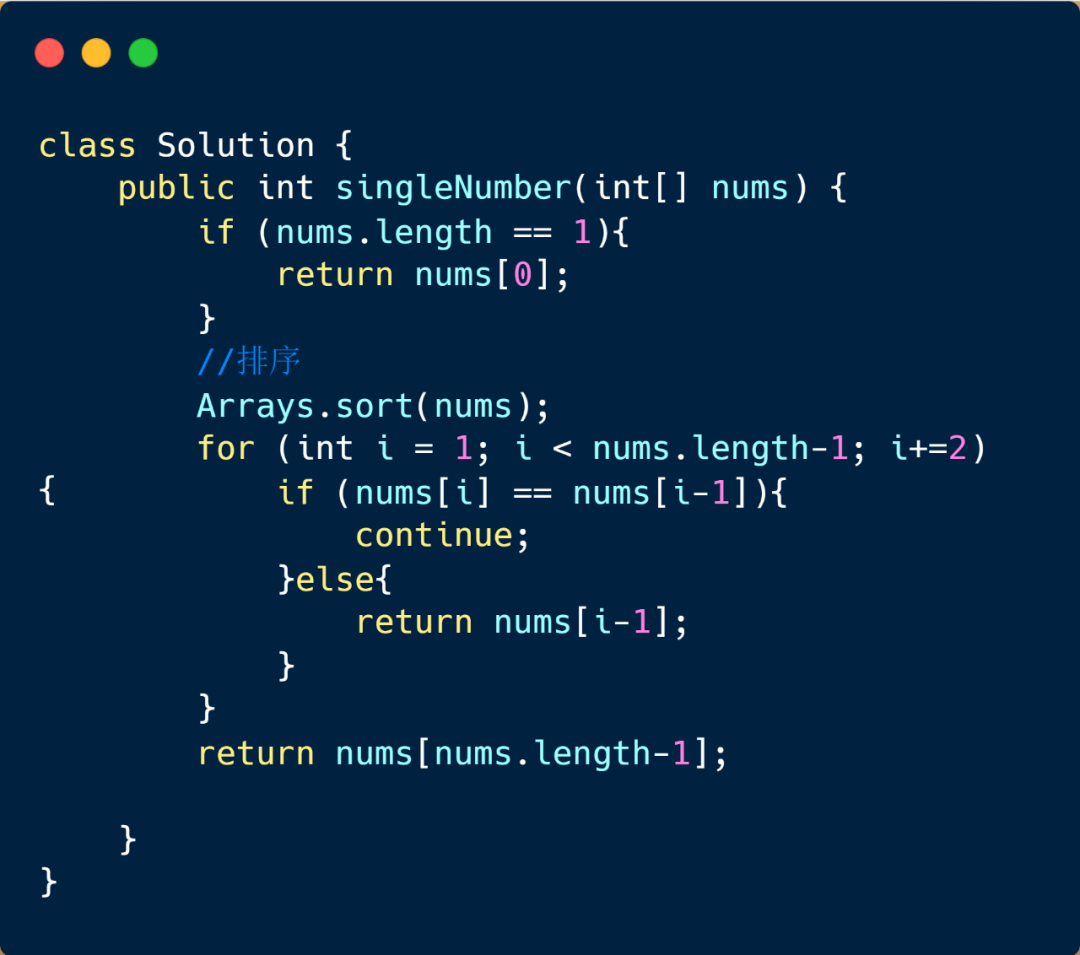
这个方法也是比较容易实现的，我们利用 HashSet 来完成。HashSet 在我们刷题时出现频率是特别高的,它是基于  HashMap 来实现的，是一个不允许有重复元素的集合。那么在这个题解中，它起到什么作用呢？

题目代码

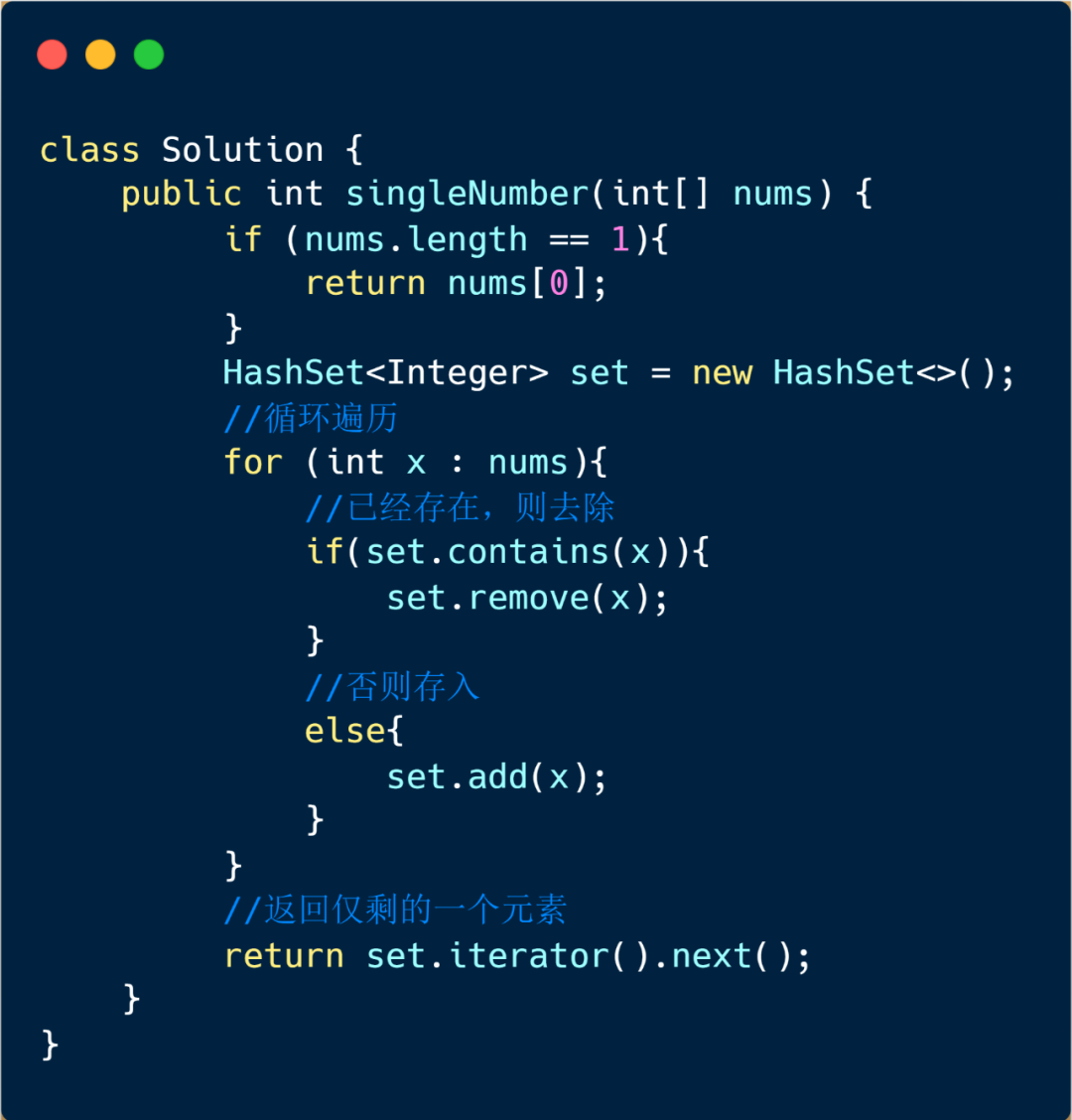
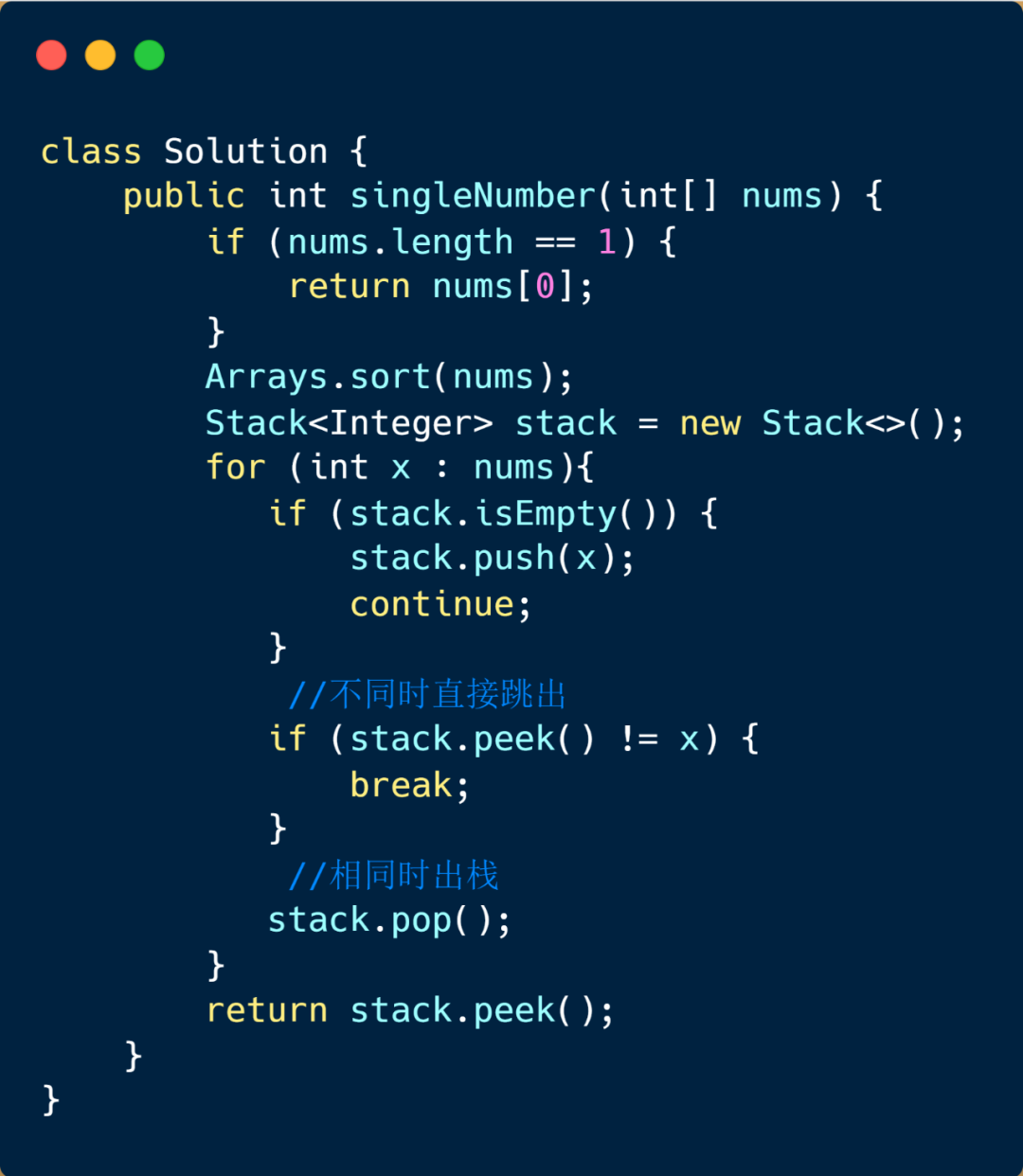
栈

该方法也很容易想到，我们首先将其排序，然后遍历数组，如果栈为空则将当前元素压入栈，如果栈不为空，若当前元素和栈顶元素相同则出栈，继续遍历下一元素，如果当前元素和栈顶元素不同的话，则说明栈顶元素是只出现一次的元素，我们将其返回即可。这个题目也可以使用队列做，思路一致，我们就不在这里说明啦。下面我们看下动图解析。

题目代码

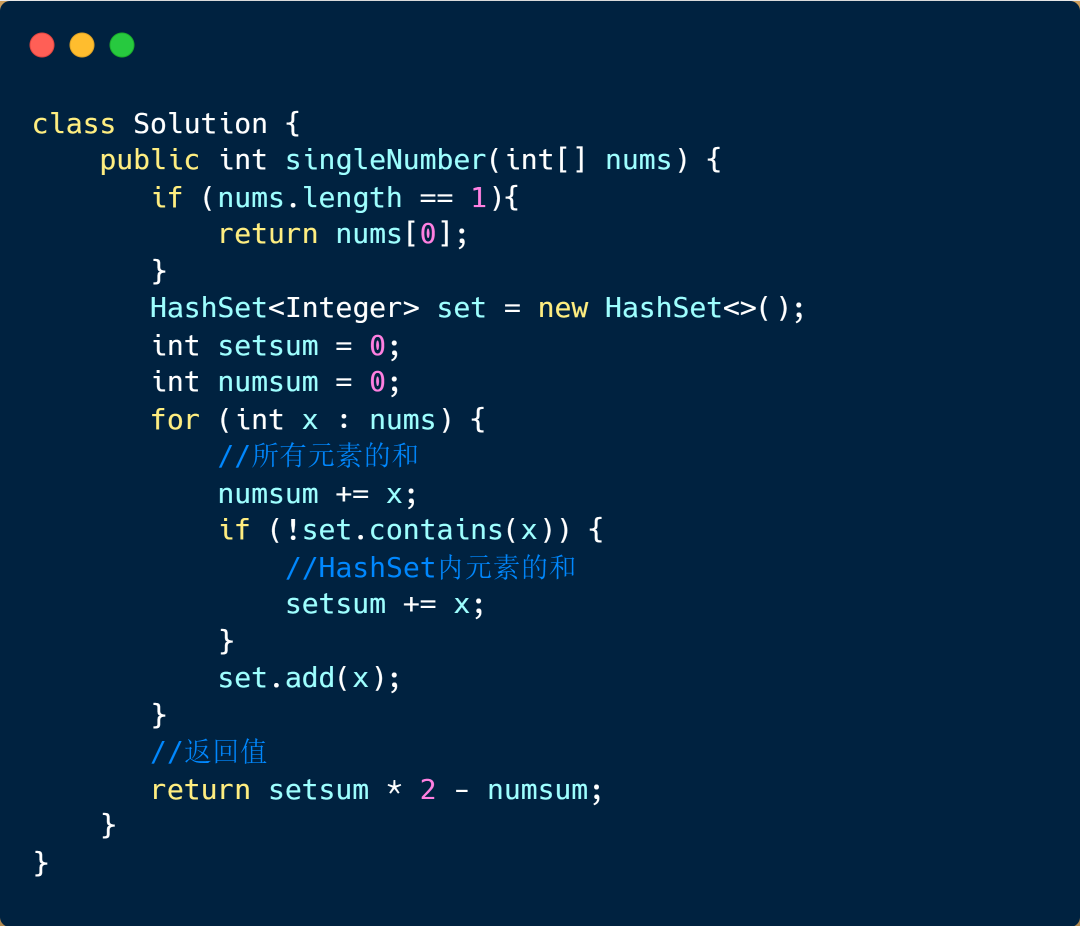
求和法

这个方法也比较简单，也是借助咱们的 HashSet 具体思路如下，我们通过 HashSet 保存数组内的元素，然后进行求和（setsum），那么得到的这个和则为去除掉重复元素的和，我们也可以得到所有元素和（numsum）。因为我们其他元素都出现两次，仅有一个元素出现一次，那我们通过 setsum * 2 - numsum 得到的元素则为出现一次的数。

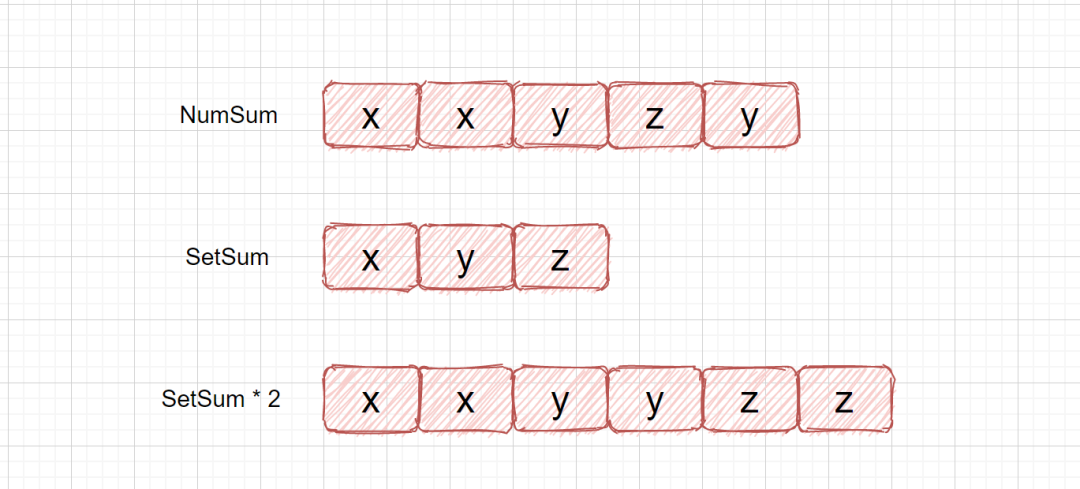
上面我们的 SetSum  * 2 - NumSum = z 也就是我们所求的值， 是不是感觉很简单呀。

题目代码

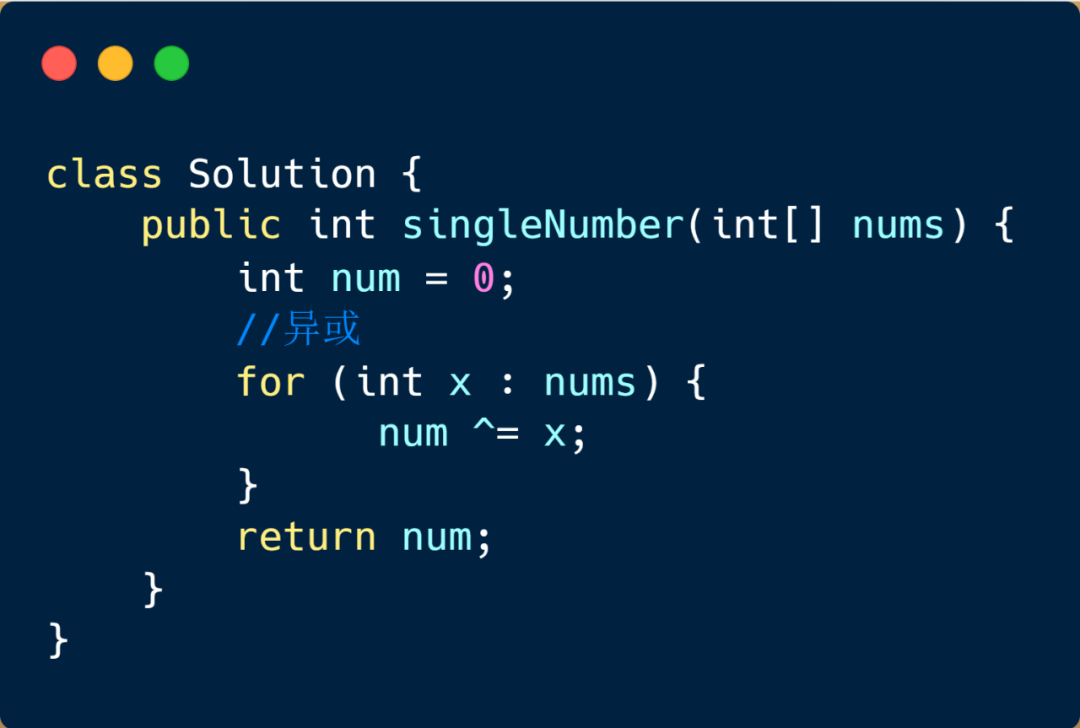
位运算

这个方法主要是借助咱们的位运算符 ^ 按位异或，我们先来了解一下这个位运算符。

按位异或(XOR)运算符“^”是双目运算符。其功能是参与运算的两数各对应的二进位相异或，当两数对应的二进位相异时，结果为1。相同时为0。

任何数和0异或，仍为本身：a⊕0 = a

任何数和本身异或，为0：a⊕a = 0 

异或运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b

例：

我们通过上面的例子了解了异或运算，对应位相异时得 1，相同时得 0，那么某个数跟本身异或时，因为对应位都相同所以结果为 0 ， 然后异或又满足交换律和结合律。则

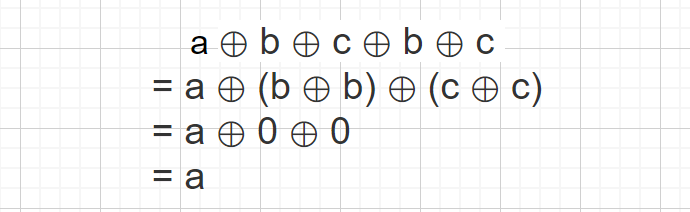
题目代码

本题一共介绍了6种解题方法，肯定还有别的方法，欢迎大家讨论。大家可以在做题的时候一题多解。这样能大大提高自己解题能力。下面我们来看一下这些方法如何应用到其他题目上。

只出现一次的数Ⅱ

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

示例 1:

输入: [2,2,3,2] 输出: 3

示例 2:

输入: [0,1,0,1,0,1,99] 输出: 99

题目很容易理解，刚才的题目是其他元素出现两次，目标元素出现一次，该题是其他元素出现三次，目标元素出现一次，所以我们完全可以借助上题的一些做法解决该题。

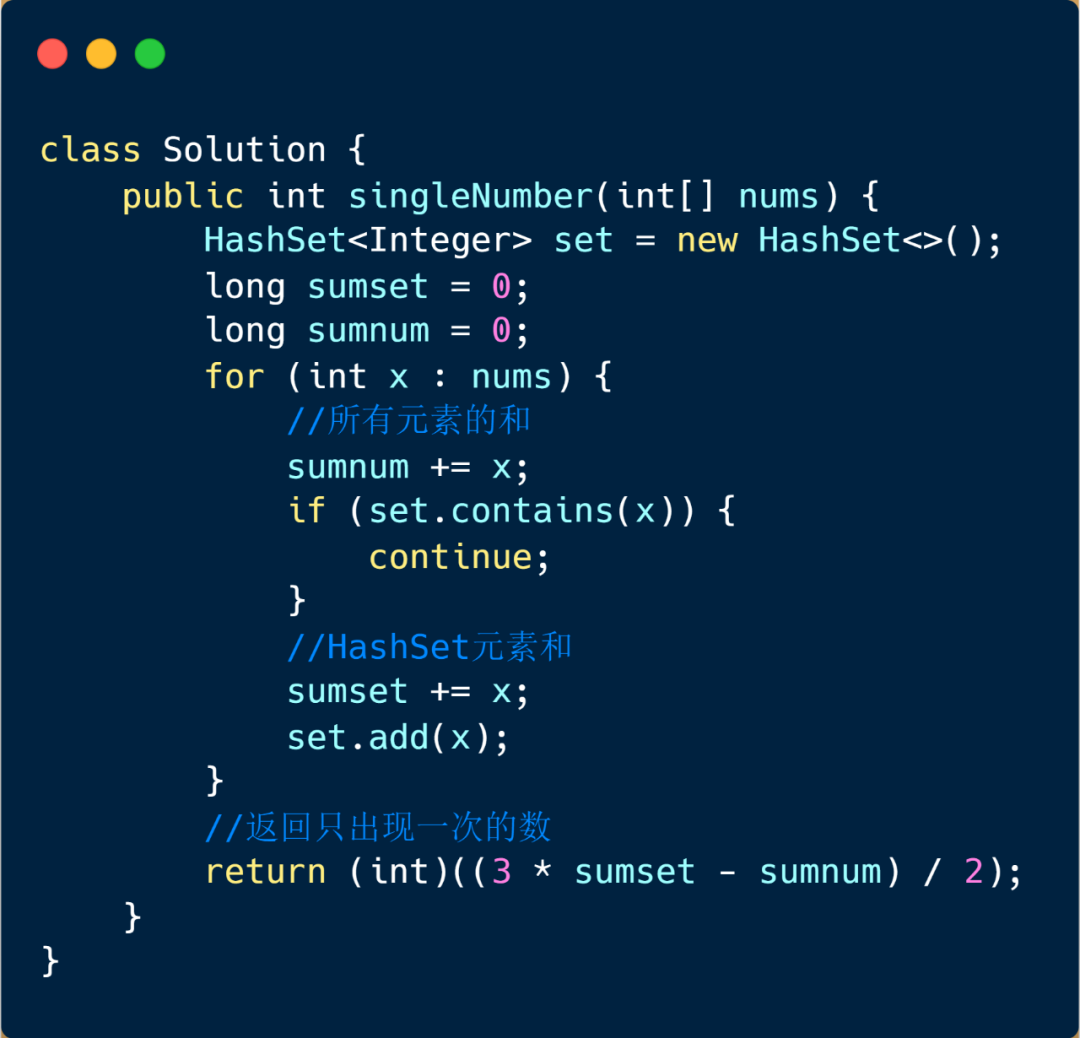
求和法

我们在上题中介绍了求和法的解题步骤，现在该题中其他元素都出现三次，我们的目标元素出现一次，所以我们利用求和法也是完全 OK 的。下面我们来看具体步骤吧。

1.通过遍历数组获取所有元素的和以及 HashSet 内元素的和。

2.（SumSet  *  3  -  SumNum）/ 2即可，除以 2 是因为我们减去之后得到的是 2 倍的目标元素。

注：这个题目中需要注意溢出的情况 。

题目代码

这个题目用 HashMap 和排序查找肯定也是可以的，大家可以自己写一下，另外我们在第一题中有个利用异或求解的方法，但是这个题目是出现三次，我们则不能利用直接异或来求解，那还有其他方法吗？

位运算

这个方法主要做法是将我们的数的二进制位每一位相加，然后对其每一位的和取余 ，我们看下面的例子。

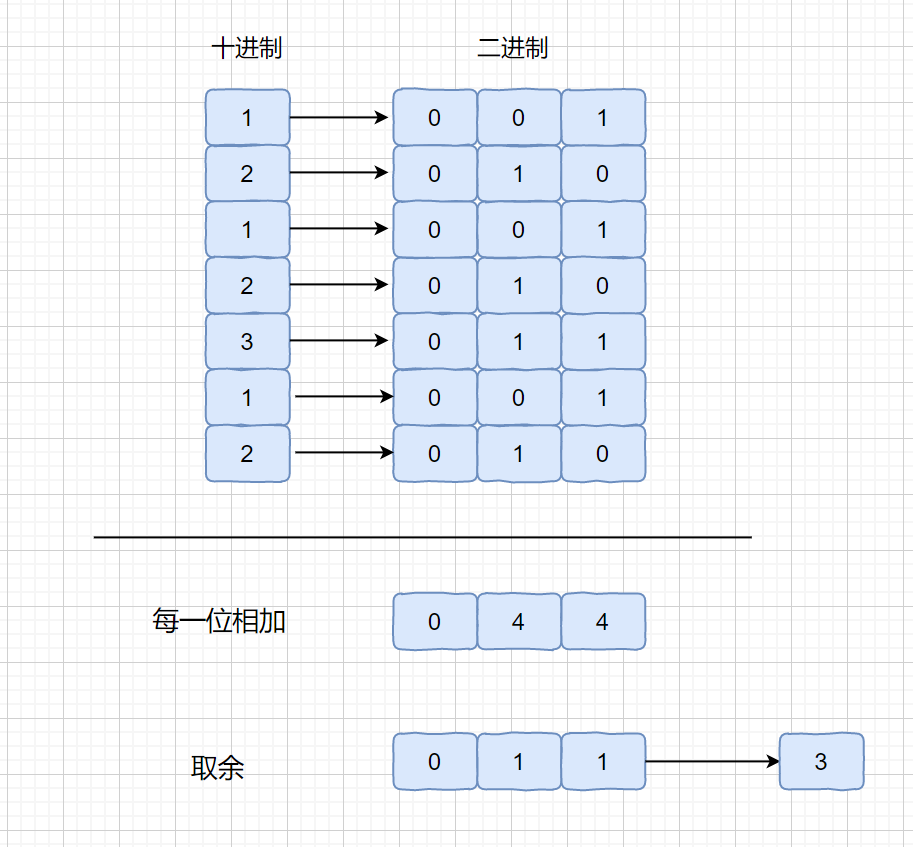
那么我们为什么要这样做呢？大家想一下，如果其他数都出现 3 次，只有目标数出现 1 次，那么每一位的 1 的个数无非有这2种情况，为 3 的倍数（全为出现三次的数） 或 3 的倍数 +1（包含出现一次的数）。这个 3 的倍数 +1 的情况也就是我们的目标数的那一位。

题目代码

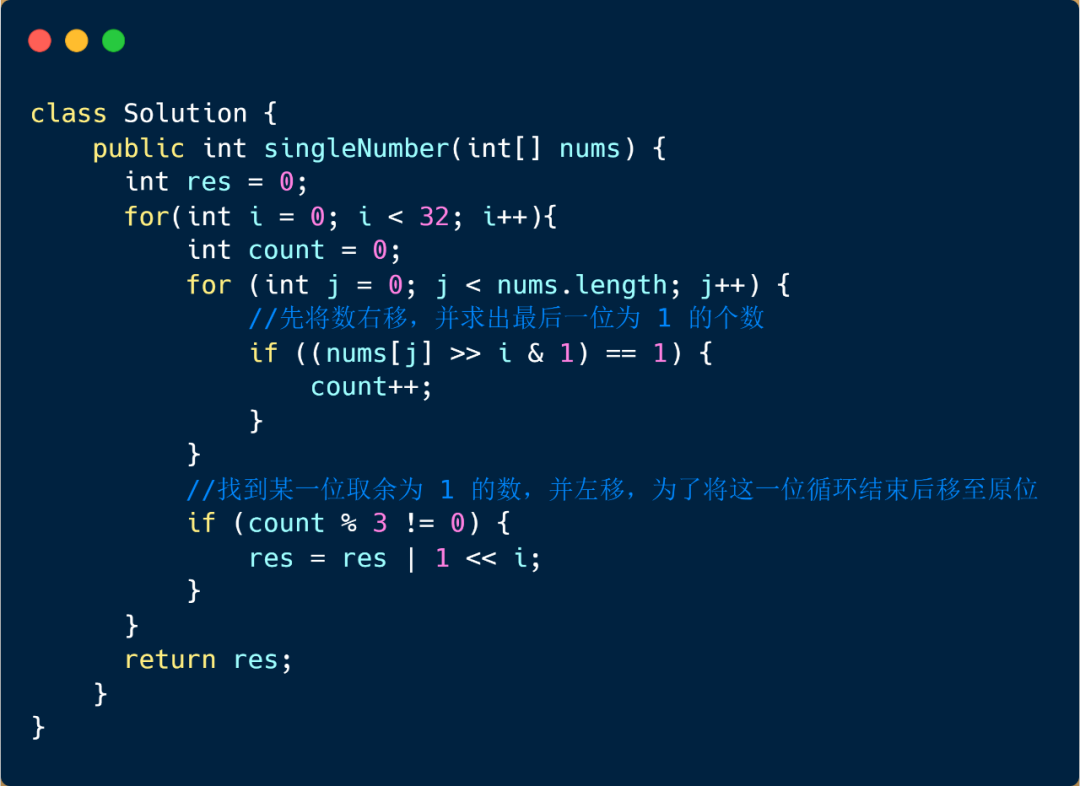
我们来解析一下我们的代码

<<     二进制左移运算符。左操作数的值向左移动右操作数指定的位数。

>>     二进制右移运算符。左操作数的值向右移动右操作数指定的位数。

另外我们的代码中还包含了 a & 1  和  a | 1 这有什么作用呢？继续看下图

&       按位与运算符：参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0

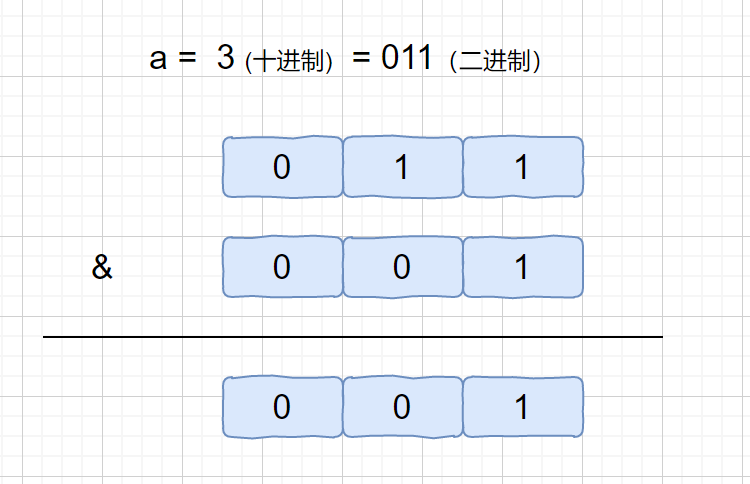
因为我们 a & 1 中 1 只有最后一位为 1，其余位皆为 0 ，所以我们发现 a & 1的作用就是判断 a 的最后一位是否为 1 ，如果 a 的最后一位为 1 ，a & 1 = 1,否则为 0 。所以我们还可以通过这个公式来判断 a 的奇偶性。

|        按位或运算符：只要对应的二个二进位有一个为1时，结果位就为1。

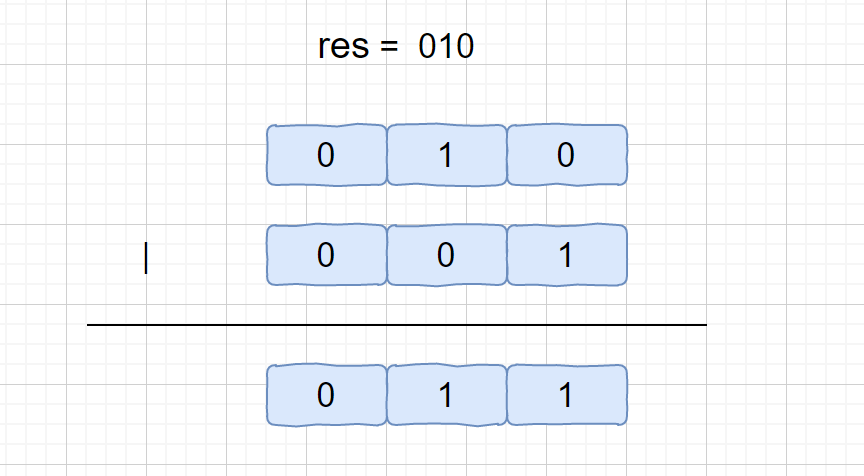
这个公式的作用就是将我们移位后的 res 的最后一位 0 变为 1。这个 1 也就代表着我们只出现一次元素的某一位。

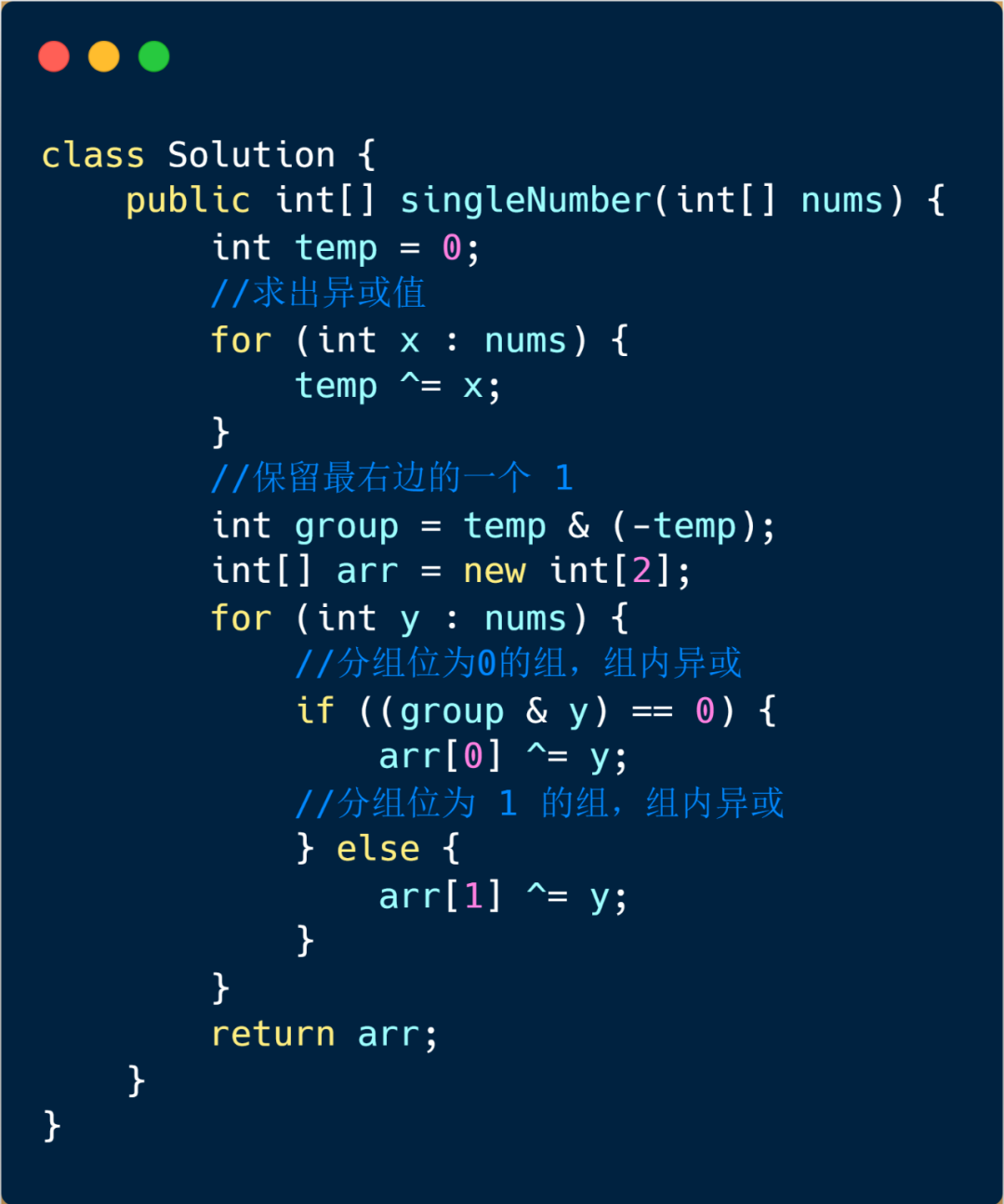
只出现一次的数Ⅲ

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。找出只出现一次的那两个元素。

示例 :

输入: [1,2,1,3,2,5] 输出: [3,5]

这个也很容易理解，算是对第一题的升级，第一题有 1 个出现 1次的数，其余出现两次，这个题目中有 2 个出现 1次的数，其余数字出现两次。那么这个题目我们怎么做呢？我们看一下能不能利用第一题中的做法解决。

HashSet

这个做法和我们第一题的做法一致，只要理解了第一题的做法，这个很容易就能写出来，有一点不同的是，第一题的 HashSet 里面最后保留了一个元素，该题保留两个元素。

题目代码

位运算

第一题中，我们可以通过异或运算直接求出目标数，但是我们第二题中不能直接用异或，是因为其他数字都出现三次，目标数出现一次。在这个题目中其他数字出现两次，目标数出现一次，但是这次的目标数为两个，我们直接异或运算的话，得到的数则为两个目标数的异或值，那么我们应该怎么做呢？

我们试想一下，如果我们先将元素分成两组，然后每组包含一个目标值，那么异或之后，每组得到一个目标值，那么我们不就将两个目标值求出了吗？

例：a,b,a,b,c,d,e,f,e,f     分组后

A组：a, a , b, b, c     异或得到 c

B组：e, e,  f,  f,  d     异或得到 d

原理懂了，那么我们应该依据什么规则对其进行分类呢？

c , d  两个不同的数，那么二进制上必定有一位是不同的，那么我们就可以根据这一位(分组位)来将 c , d 分到两个组中，数组中的其他元素，要么在 A 组中，要么在 B 组中。

我们应该怎么得到分组位呢？

我们让 c , d 异或即可，异或运算就是对应位不同时得 1 ,异或之后值为 1 的其中一位则为我们分组。

例 001 ⊕  100 = 101，我们可以用最右边的 1 或最左边的 1 做为分组位，数组元素中，若我们将最右边的 1 作为我们的分组位，最后一位为 0 的则进入 A 组，为 1 的进入 B 组。

那么我们应该怎么借助分组位进行分组呢？

我们处理 c , d 的异或值，可以仅保留异或值的分组位，其余位变为 0 ，例如 101 变成 001或 100

为什么要这么做呢？在第二题提到，我们可以根据 a & 1 来判断 a 的最后一位为 0 还是为 1，所以我们将 101 变成 001 之后，然后数组内的元素  x & 001  即可对 x 进行分组 。同样也可以 x & 100 进行分组.

那么我们如何才能仅保留分组位，其余位变为 0 呢？例 101 变为 001

我们可以利用 x & (-x) 来保留最右边的 1

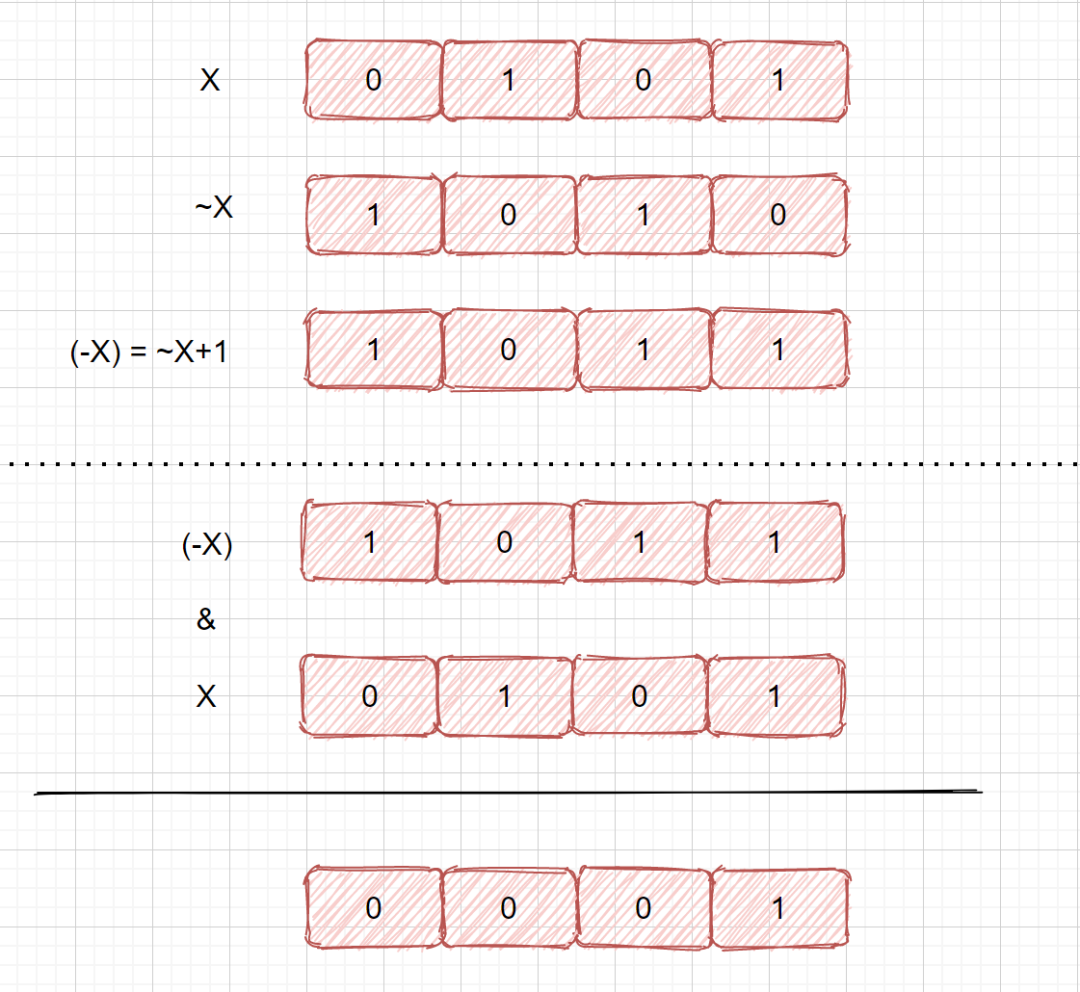
题目代码：