旷视MegEngine是如何将31*31的大核卷积计算速度提高10倍的-技术圈

来源：DeepHub IMBA
本文约3400字，建议阅读5分钟
“大内核的cnn可以胜过小内核的cnn”这可能是今年来对于CNN研究最大的成果了。

2021年提议的Vision Transformer（VIT）已成为计算机视觉深度学习领域的一个有前途的研究主题。随着VIT的研究变得更加深入，一些研究人员受到VIT的大型接收领域的启发，将卷积网络也改造成具有更大的接收场来提高效率。根据有效的接收场（ERF）理论，ERF的大小与内核大小和模型深度的平方根成正比。这意味着通过堆叠层来实现大ERF的有效性不如增加卷积内核大小。因此，研究人员提出了包含大型卷积内核新的CNN结构。该网络可以达到与VIT相同的准确性。“大内核的cnn可以胜过小内核的cnn”这可能是今年来对于CNN研究最大的成果了。

内核带来了更多的计算和参数

CNN中最常见的卷积内核大小是3x3、5x5、7x7。一般情况下如果卷积内核的大小超过9x9就将其确定为“大”。卷积内核的大小增加了n，参数数量和浮点操作（FLOPS）的数量将大约增加n平方。这就是研究人员在探索CNN新结构时首先不考虑大型内核卷积的主要原因。如下图所示，逐通道卷积(又称深度卷积)可以将FLOPs和参数数量减少到密集卷积的1/(输入通道数量)。这就是为什么大多数研究人员将大核卷积设计为深度卷积，这样既可以获得大核卷积的好处，又不需要大幅增加参数和FLOPs。

但是在相同的FLOPs限制下，研究人员发现，他们的大核深度卷积神经网络比传统的网络运行得慢得多。

MegEngine团队发现，通过适当的优化，当内核尺寸越来越大时，深度卷积几乎不需要任何成本。本文就是对他们研究成果的介绍。

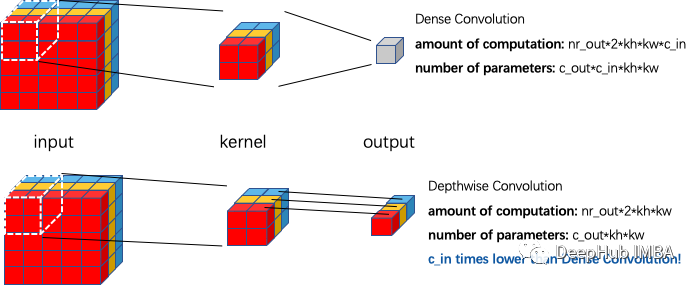
如何寻找大核卷积的优化空间?

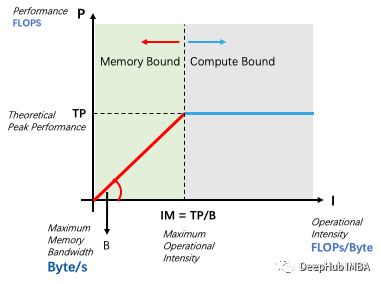
为了回答这个问题，我们需要将Roofline 模型作为背景。如下图所示，roofline模型用于描述在计算平台的算力和带宽的限制下，程序所能达到的理论性能上界。

roofline模型的示意图，有三个重要概念：

算力：每秒所完成的浮点运算次数，单位为FLOP/s或GFLOP/s
带宽：每秒所完成的内存读取量，单位为Byte/s或GByte/s
计算密度：又称访存比，是算力与带宽的比值，即每字节读取所完成的浮点运算量，单位为FLOP/Byte

“roofline”是指TP对IM的图的形状。设备的理论峰决定了“屋顶”的高度（蓝线）。同时，“屋顶”（红线）的斜率是设备的最大访问带宽。这两条彩色线的连接也分隔两种类型的应用，计算结合和内存结合的瓶颈的分离。

当应用程序的计算密度I超过最大IM时，其性能只能达到计算设备的理论峰值TP。应用程序的最大性能P显然与计算密度I成正比。这种类型的应用程序称为计算绑定。当应用程序的计算密度小于IM时，性能是由设备的最大带宽和计算密度确定的。这种类型的应用程序称为内存绑定。与计算绑定方案相反，增加设备带宽或增加内存绑定应用程序的计算密度可能会导致应用程序性能的线性增加。

针对密集卷积的优化已经达到了瓶颈

到现在为止，很多的研究已经探索对密集卷积的优化技术，包括Direct, im2col/implicit GEMM, Winograd and FFT。

在本文中使用NVIDIA 2080TI GPU作为计算设备在roofline模型的背景下进行分析。该计算设备的L2高速缓存带宽为2.16TB/s，理论峰值性能为4352 FFMA核心 * 1.545 GHz * 2 = 2 = 13.447 tflops。我们假设CUDA中每个线程的输出数据都积累在寄存器中，L1缓存达到100%，同时忽略了写回输出的过程。由于现代计算设备的设计足以在实际卷积计算中同时支持许多耗时的访问操作，还假设L2缓存达到100%，并达到L2缓存的最大带宽。本文使用的卷积输入形状为(n, ic, ih, iw)。内核是(oc, ic, kh, kw)，输出是(n, oc, oh, ow)。

im2col/implicit GEMM是最经典的密集卷积优化方法，在im2col转换之后，将卷积转换为一个矩阵乘法问题，其中𝑀=oc，𝑁=𝑛×oh×ow，𝐾=ic×kh×kw，如下图所示。

矩阵乘法在cuBLAS等计算库中已经得到了很好的优化。特别是当矩阵足够大时，性能可以接近设备的理论峰。我们在此简要分析了使用Roofline模型的性能。

为了充分利用硬件结构，通常将矩阵乘法的计算划分为块，这样可以使多级存储能够满负荷工作，从而获得最大的内存访问带宽。

如下图所示，给定CUDA中的每个Thread Block处理BM×BN的输出：

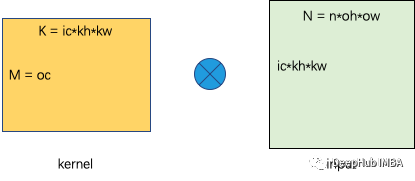
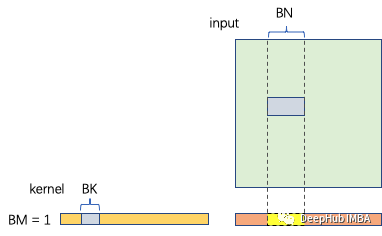
内核块大小为BM×BK
输入块大小为BK×BN
计算的次数是BM×BN×BK×2
内存访问为(BM×BK+BN×BK)×4
计算密度为BM×BN×2/(BM+BN)×4

根据Roofline模型的描述，设备的IM计算为IM=TP/𝐵=13.447/2.16=6.225 FLOPs/byte。为了达到硬件的理论峰值，我们只需要保证计算密度大于IM即可。设BM=32, BN=32，则计算密度达到8 FLOPs/byte，明显大于IM。但是该应用程序属于Compute Bound区域，这意味着没有性能优化的空间。我们可以肯定地得出VGG时代的旧结论：“随着内核尺寸的增长，时间也是线性的增加”。

Depthiswise Conv不是同一情况

随着内核大小的增长，计算的数量随着密度或深度的增长而增长。由于Cudnn在Depthiswise Conv上的性能趋势确实显示出类似的结论，因此许多人认为先前关于密集的Conv的结论在Depthiswise Conv上也有效。

这其实是错误的归纳总结，因为Depthiswise Conv的前提条件就核传统的密集卷积不一样。

我们用im2col/implicit GEMM 方法分析Depthiswise Conv。由于Depthiswise Conv会逐通道的计算，因此可以将其视为一组单通道卷积，通道数等于组的大小。在IM2COL转换之后，我们将获得一个批处理的GEMV，对于下图所示。

保持与密集块相同的块大小，每个批的GEMV如下图所示。此时的计算密度为BN×2/(1+𝐵𝑁)×4=BN/(2×BN+2)。给定BN=1，最大计算密度为0.25 FLOPs/byte，远小于IM 6.225。这意味着现在在内存限制区。尽管有一些方法可以使GEMV更快，但“向量x矩阵”的布局注定是内存受限的应用程序。

接下来，我们将分析Direct方法。例如，让一个warp的所有32个线程都计算输出oh*ow，内核大小为kh*kw:

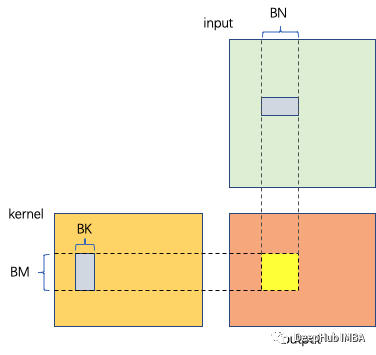
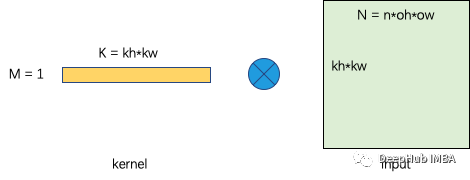
浮点运算次数=oh×ow×khkw×2 FLOPs
内存访问数= (kh×kw+(oh+kh−1)×(ow+kw−1))×4 bytes
内核大小:kh×kw
输入大小:(oh+kh−1)×(ow+kw−1)
计算密度=(oh×ow×kh×kw×2)/{(kh×kw+(oh+kh−1)×(ow+kw−1))×4}

如果每个线程计算4个输出，那么当内核大小为3x3时，一次warp可以计算4x32个输出。此时计算密度为(4×32×3×3×2)/(3×3+6×34)×4=2.7 FLOPs/byte。最大性能为2.16*2.7 = 5.84 TFLOPS远低于13.447 TFLOPS的理论峰值。所以为了增加计算密度可以增加每次经纱计算的输出次数。但是由于卷积本身的输出大小以及有限的计算资源（例如每个流多处理器中的寄存器文件），所以并不能无限的增加。

总结一下在im2col和direct方法中的发现:深度卷积是一种Memory Bound操作。增加内核大小不会大幅改变内存访问的数量，计算的时间应该保持不变，这就是他与传统的密集卷积最大的区别。但是上面的研究的好的方向是在适当的优化下，深度卷积的内核大小几乎可以随意增加。

MegEngine的表现

与理论分析不同的是，在实际应用是发现随着内核大小的增加，cuDNN的性能会变得很差。

输入形状：(64,384,32,32)

输出形状：(64,384,32,32)

设备：2080 ti

这就是MegEngine针对大核深度卷积进行密集优化的原因，如果增加核的大小，需要使计算时间与理论预测的一样。与PyTorch相比，使用MegEngine时训练时间仅为10%。

有兴趣的话可以看看旷视的MagEngine

https://github.com/MegEngine/MegEngine


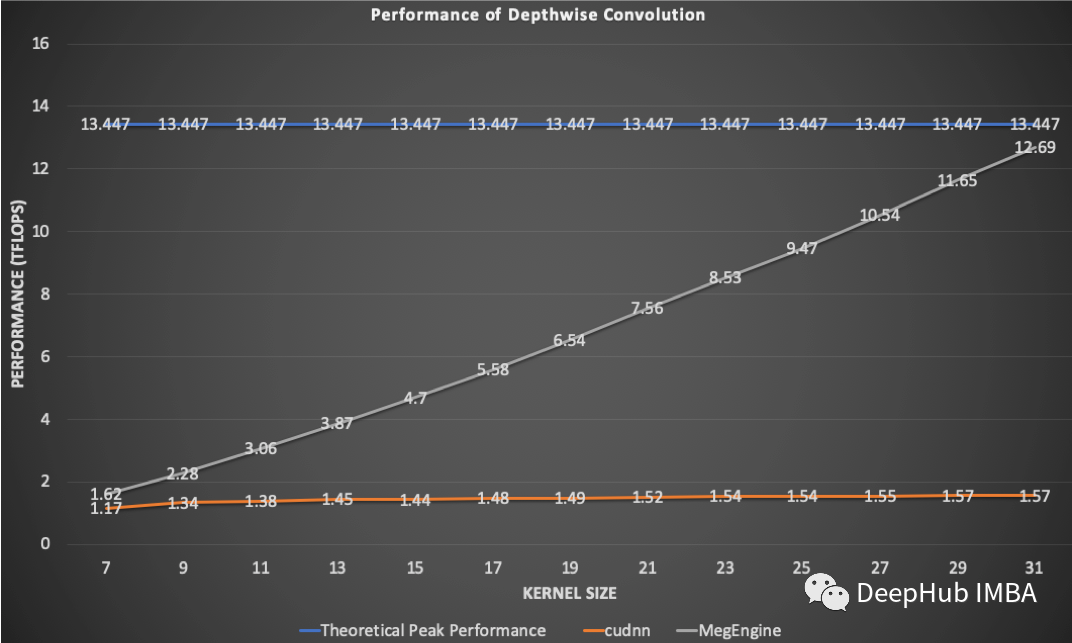
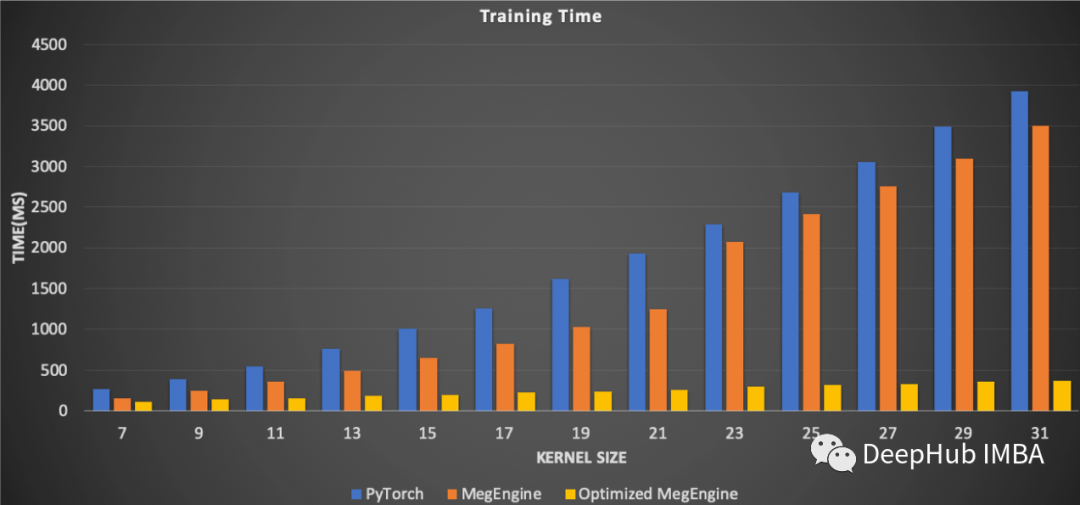
编辑：黄继彦