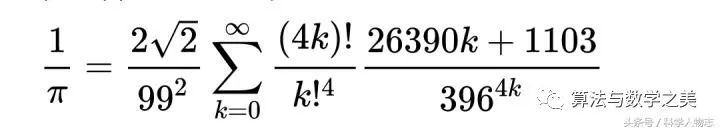先声明下,利益相关,因为服务的客户里面刚好就有淘宝和京东,顺丰,艺龙等。要回答这个问题,先看看这个图。
大部分公的短信服务都是这样的模式。
1、首先企业应用层、这里面就很多啦,验证码啦,订单通知啦,反正各种需要应用到短信服务的。各行各业都不一样,比如顺丰下单收件通知,签收短信等。
2、一般都设有短信服务器,对信息进行优先排列,提交到通道,进行上行短信接收,状态接收等。大的公司甚至有自己的MAS服务器。
3、短信提交有的是通过第三方,第三方一般是10690开头的三网通道,走第三方优势是价格便宜,通道资源丰富,一般第三方都在全国多个省份,多个运营商落地。短信服务器提交到第三方通道大部分走公网。IP绑定等方式解决安全性问题。
4、有的是自






 下载APP
下载APP