18 个常犯的统计学错误，避坑防雷指南！

1变量之间关系可以分为两类

函数关系：反映了事务之间某种确定性关系；

相关关系：两个变量之间存在某种依存关系，但二者并不是一一对应的；反映了事务间不完全确定关系。

2为什么要对相关系数进行显著性检验？

实际上完全没有关系的变量，在利用样本数据进行计算时也可能得到一个较大的相关系数值（尤其是时间序列数值）

当样本数较少，相关系数就很大。当样本量从100减少到40后，相关系数大概率会上升，但上升到多少，这个就不能保证了；取决于你的剔除数据原则，还有这组数据真的可能不存在相关性；

改变两列数据的顺序，不会对相关系数，和散点图（拟合的函数曲线）造成影响；对两列数据进行归一化处理，标准化处理，不会影响相关系数；我们计算的相关系数是线性相关系数，只能反映两者是否具备线性关系。相关系数高是线性模型拟合程度高的前提；此外相关系数反映两个变量之间的相关性，多个变量之间的相关性可以通过复相关系数来衡量；

3增加变量个数，R2会增大；P值，F值只要满足条件即可，不必追求其值过小

4多重共线性与统计假设检验傻傻分不清？

多重共线性与统计假设没有直接关联，但是对于解释多元回归的结果非常重要。相关系数反应两个变量之间的相关性；回归系数是假设其他变量不变，自变量变化一个单位，对因变量的影响，而存在多重共线性（变量之间相关系数很大），就会导致解释困难；比如y~x1+x2；x1与x2存在多重共线性，当x1变化一个单位，x2不变，对y的影响；而x1与x2高度相关，就会解释没有意义。

一元回归不存在多重共线性的问题；而多元线性回归要摒弃多重共线性的影响；所以要先对所有的变量进行相关系数分析，初步判定是否满足前提---多重共线性。

5时间序列数据会自发呈现完全共线性问题，所以我们用自回归分析方法

6什么样的模型才是一个好模型？

在测试集表现与预测集相当，说明模型没有过度拟合：在训练集上表现完美，在测试集上一塌糊涂。

原因：模型过于刚性，“极尽历史规律，考虑随机误差”；拟合精度不能作为衡量模型方法的标准。

一个好的模型：只描述规律性的东西（抓住事务的主要特征），存在随机误差是好事，在预测时，就有了“容错空间”，预测误差可能减小！

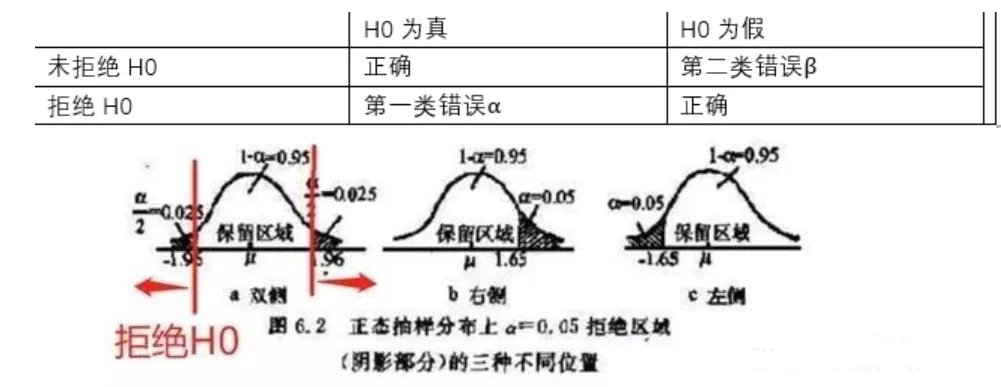
7假设检验显著性水平的两种理解

显著性水平：

通过小概率准则来理解，在假设检验时先确定一个小概率标准----显著性水平；用表示；凡出现概率小于显著性水平的事件称小概率事件。

通过两类错误理解：为拒绝域面积

8中心极限定律与大数定理

大数定理---正态分布的“左磅”，随着样本数的增加，样本的平均值可以估计总体平均值。

中心极限定理---正态分布的“右臂”具有稳定性，大数定理说明大量重复实验的平均结果具有稳定解决了变量均值的收敛性问题中心极限定理说明随机变量之和逐渐服从某一分布，解决了分布收敛性问题。

9方差

方差能最大程度的反映原始数据信息。

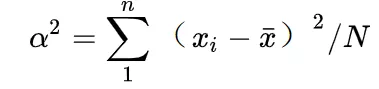
反映了一组数据相对于平均数的波动程度，相比于，其平方项更放大了波动，且差的平方在数学公式推导上有大用。

10使用最小二乘法条件

• 自变量之间不能存在完全共线性。

• 总体方程误差项服从均值为0的正态分布（大数定理）。

• 误差项的方差不受自变量影响且为固定值（同方差性）。

11最大似然估计与最小二乘法区别

• 最小二乘法是基于几何意义上距离最小。

• 最大似然估计是基于概率意义上出现的概率最大。

• 最小二乘法：对数据分布无要求。

• 最大似然估计：需要知道概率密度函数。

12关于H0与H1

H0：原假设，零假设----零是相关系数为0，说明两个变量无关系。

H1:备用假设。

如何设置原假设：

1）H0与H1是完备事件组，相互对立，有且只有一个成立。

2）在确立假设时，先确定备设H1，然后再确定H0，且保证“=”总在H0上。

3）原H0一般是需要反驳的，而H1是需要支持的4）假设检验只提供原假设不利证据。

即使“假设”设置严密，检验方法“精确”；假设检验始终是建立在一定概率基础上的，所以我们常会犯两类错误。

第一类：原H0是真，却拒绝原假设；犯类错误。

第二类：原H0是假，却不拒绝原假设；犯类错误。

通常只能犯两种错误中的一种，且增加，减少。

通常，类错误是可控的，先设法降低第一类错误概率。

13什么是双尾检验，单尾检验？

1） 当H0采用等号，而H1采用不等号，双尾检验。

2）当H0是有方向性的，单尾检验。

14P值

当原假设为真时，比所得到的样本观察，结果更极端的结果会出现的概率。

如果P值很小，我们拒绝原假设的理由越充分。

P的意义不表示两组差别大小，p反映两组差别有无统计学意义。

显著性检验只是统计结论，判断差别还需要专业知识。

15T检验与U检验

• 当样本容量n够大，样本观察值符合正态分布，可采用U检验。

• 当样本容量n较小，若观测值符合正态分布，可采用T型检验。

16方差分析

主要用于两样本及以上样本间的比较，又被称为F检验，变异数分析。

基本思想：通过分析研究不同来源的变异对总体变异的贡献大小，从而确定可控因素对研究结果影响力的大小。

总变异可以被分解为组间变异与组内变异。

组间变异：由于不同实验处理而造成的各组之间的变异。

组内变异：组内各被适变量的差异范围所呈现的变异。

17直方图：对数据进行整体描述，突出细节

箱线图：对数据进行概要描述，或对不同样本进行比较。箱线图可以让我们迅速了解数据的汇集情况（这个样本，紧密的集合在一起；哇，这个样本不那么密集；这个样本，大部分向左偏，哇，这个样本大部分向右偏）。

但是请注意：一个直方图比1000个p值更重要，拿到数据先绘制散点图、直方图、箱线图看看，再决定用什么描述！

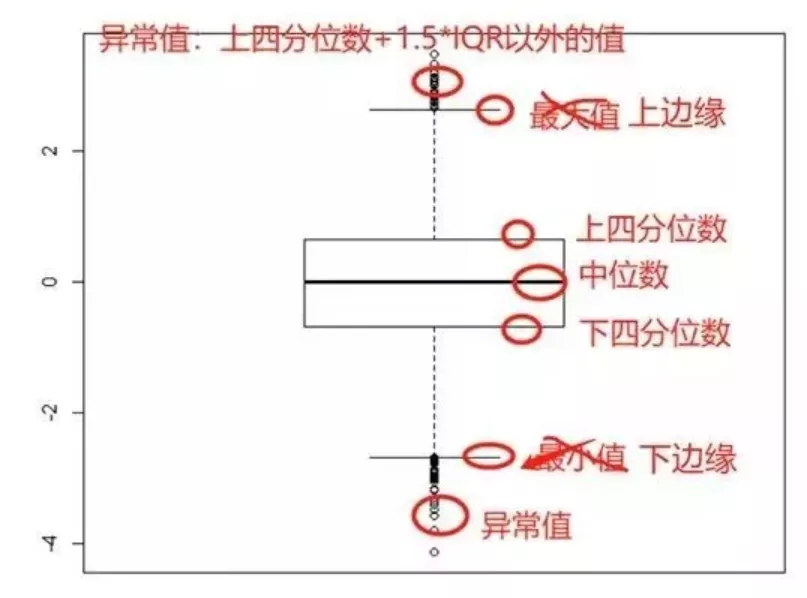
18箱线图

对于分位数的理解：霜线图看数据分布特征统计学中，把所有数值由小到大排列并分成四等份，处于三个分割点位置的得分就是四分位数。所以，四分位数有三个！四指四等份！

第一四分位数：下四分位数；等于该样本中所有数值由小到大排列后第25%的数字（所以下四分位数可以不是样本中的数值，它是一个统计指标（就像平均数一样，不一定是原数据中的一点）。

第二四分位数：中位数

第三四分位数：上四分位数

其中，下四分位数与上四分位数的距离叫四分位距！（IQR）

一元回归不存在多重共线性的问题；而多元线性回归要摒弃多重共线性的影响；所以要先对所有的变量进行相关系数分析，初步判定是否满足前提---多重共线性。

本文内容参考以上网址。以上内容仅供学习使用，不作其它用途，如有侵权，请留言联系，作删除处理！

有任何疑问及建议，扫描以下公众号二维码添加交流：