​LeetCode刷题实战261：以图判树

示例 1：

输入: n = 5, 边列表 edges = [[0,1], [0,2], [0,3], [1,4]]
输出: true

示例 2:

输入: n = 5, 边列表 edges = [[0,1], [1,2], [2,3], [1,3], [1,4]]
输出: false

注意：你可以假定边列表 edges 中不会出现重复的边。由于所有的边是无向边，边 [0,1] 和边 [1,0] 是相同的，因此不会同时出现在边列表 edges 中。

class Solution {
    public boolean validTree(int n, int[][] edges) {
        //构建邻接矩阵
        int[][] graph = new int[n][n];
        //有边的元素设置为1，没有边的元素设置为0
        for (int[] edge : edges) {
            // graph[3][4] == 1 表示 3 和 4 是连接的
            graph[edge[0]][edge[1]] = 1;
            graph[edge[1]][edge[0]] = 1;
        }
        //进行BFS
        Queue<Integer> queue = new LinkedList<>();
        //从第一个节点开始搜索，这样就不会漏掉无边图的情况
        queue.add(0);
        boolean[] visited = new boolean[n];
        while (!queue.isEmpty()) {
            Integer cur = queue.poll();
            visited[cur] = true;
            //获取邻接点
            for (int i = 0; i < n; i++) {
                //查看当前节点的邻接点
                if (graph[cur][i] == 1) {
                    if (visited[i]) {
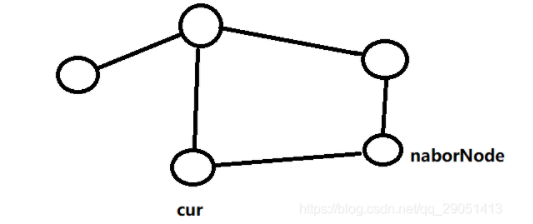
                        // cur 的邻接节点居然被处理过
                        // 说明 cur 和 i 在前面有一个共同的父结点
                        // 加上 cur 和 i 又是连在一起的
                        // 说明存在环
                        return false;
                    }
                    visited[i] = true;
                    //涂黑访问过的节点
                    graph[cur][i] = 0;
                    graph[i][cur] = 0;
                    queue.add(i);
                }
            }
        }

        //判断是否为单连通分量
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                // 居然还有一个节点没有被访问过，说明不是图
                return false;
            }
        }
        return true;
    }
}