弹簧秤称球问题算法分析及程序模拟
一、抛出问题

一开始大家都以为是传统的无砝码天平称球问题,想用分治算法来解决。在赵军老师的提示之后,才发现弹簧秤和无砝码天平的区别:弹簧秤是可以称量出小球的具体重量的,而且题目要求求出每个球的具体重量。
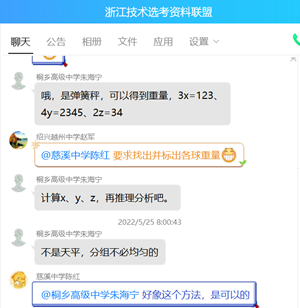
朱老师把小球依次编号1-6,分成3次称量,第一次将球1,2,3合在一起称,第二次将球2,3,4,5合在一起称,第三次将球3,4合在一起称,可以表示为:3x=123,4y=2345,2z=34。
一开始我没怎么看懂,发现朱老师提供的表达式中没有出现6号球,心里就产生了疑问,万一6号球是异球呢?不称量它怎么得出异球的重量?于是随口说了一句:@桐乡高级中学朱海宁 有6个球哦。
朱老师耐心地回答我:可以推出来的,比如x=y,那就是6号球有问题,单独称一下就好。
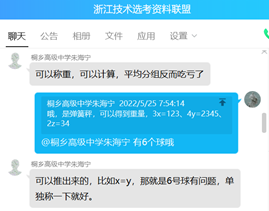
我又继续思考了x!=y的情形,发现可以轻松地推导出异球为1和5的情形,即当y=z时,异球为1;当x=z时,则异球为5。
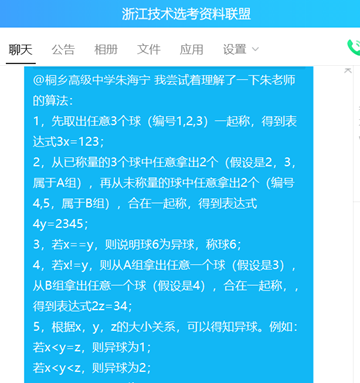
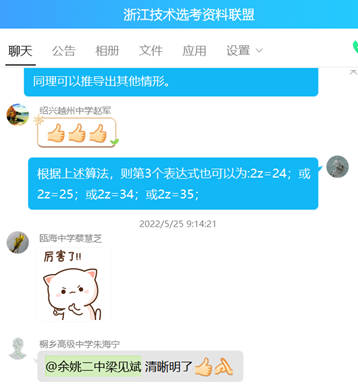
五、程序模拟
事情到这里似乎已经结束了。但只提出算法,不编写程序不是我的风格。不把事情完全做好我是不会罢休的。于是我决定编写程序实现算法功能。
这是我的第一版程序:
def fun_1(a):x = sum(a[:3]) # 第一次称重:3x=123y = sum(a[1:5]) # 第二次称重:4y=2345if x/3 == y/4: # 前面5个球等重,则球6为异球z = a[5] # 第三次称重:称量异球6print(f"异球为6,其重量为{z},其他球重量为{x//3}")else:z = a[2] + a[3] # 第三次称重:2z=34if y/4 == z/2: # 异球为1print(f"异球为1,其重量为{x-z},其他球重量为{z//2}")elif x/3 == z/2: # 异球为5print(f"异球为5,其重量为{y-x},其他球重量为{z//2}")elif x/3 < y/4 < z/2 or x/3 > y/4 > z/2: # 异球为2print(f"异球为2,其重量为{y-3*z//2},其他球重量为{z//2}")elif z/2 < y/4 < x/3 or z/2 > y/4 > x/3: # 异球为4print(f"异球为4,其重量为{z-x//3},其他球重量为{x//3}")else: # 异球为3print(f"异球为3,其重量为{2*z-x},其他球重量为{x-z}")import randomfor i in range(16):a = [3] * 6 # 初始化每个小球重量均为3num = random.randint(0, 5) # 选择任意一个小球为异球a[num] = a[num] + random.choice([-1,1]) #异球重量可轻可重print(a)fun_1(a, 2, 4)

我增加循环次数,又测了好几次,发现其他小球为异球时都是对的,就是4号球出错。
为什么4号球总是出错呢?我又看了看测试结果,发现程序总是把4号球错认为2号球。
这说明什么问题呢?
会不会是因为先判断2号球,再判断4号球的缘故?我尝试着把多分支语句中elif语句的位置换了一下,让程序先判断4号球,再判断2号球。

原来问题出在这里!
2号球和4号球到底谁才是异球?条件表达式怎么会一模一样呢?是我漏掉了什么东西吗?
再仔细看看算法分析。咦,我好像发现了点什么。
当异球为2时,4号球是普通球,则z应该为整数;同理,当异球为4时,2号球是普通球,则x应该为整数。
妙啊!这是属于我的尤里卡时刻!
好了,现在只需要加上两个限制条件就行了,第二版程序如下:
def fun_2(a):x = sum(a[:3]) # 第一次称重:3x=123y = sum(a[1:5]) # 第二次称重:4y=2345if x/3 == y/4: # 前面5个球等重,则球6为异球z = a[5] # 第三次称重:称量异球6print(f"异球为6,其重量为{z},其他球重量为{x//3}")else:z = a[2] + a[3] # 第三次称重:2z=34if y/4 == z/2: # 异球为1print(f"异球为1,其重量为{x-z},其他球重量为{z//2}")elif x/3 == z/2: # 异球为5print(f"异球为5,其重量为{y-x},其他球重量为{z//2}")elif z/2 == z//2 and (x/3 < y/4 < z/2 or x/3 > y/4 > z/2): # 异球为2print(f"异球为2,其重量为{y-3*z//2},其他球重量为{z//2}")elif x/3 == x//3 and (z/2 < y/4 < x/3 or z/2 > y/4 > x/3): # 异球为4print(f"异球为4,其重量为{z-x//3},其他球重量为{x//3}")else: # 异球为3print(f"异球为3,其重量为{2*z-x},其他球重量为{x-z}")

八、精益求精
现在,问题应该说得到完美解决了。但解决问题从来都没有最好,只有更好。
第三次称量的方式有4种,我只考虑了其中一种。另外3种的结果是不是和前面一致?我还没有编程验证。这件事情不做好,就不算完。
于是,秉着精益求精的精神,追求完美的我又给出了第三版程序:
def fun_3(a, i, j):x = sum(a[:3]) # 第一次称重:3x=123y = sum(a[1:5]) # 第二次称重:4y=2345if x/3 == y/4: # 前面5个球等重,则球6为异球z = a[5] # 第三次称重:称量异球6print(f"异球为6,其重量为{z},其他球重量为{x//3}")else:z = a[i-1] + a[j-1] # 第三次称重:2z=24或25或34或35if y/4 == z/2: # 异球为1print(f"异球为1,其重量为{x-z},其他球重量为{z//2}")elif x/3 == z/2: # 异球为9-jprint(f"异球为{9-j},其重量为{y-x},其他球重量为{z//2}")elif z/2 == z//2 and (x/3 < y/4 < z/2 or x/3 > y/4 > z/2): # 异球为5-iprint(f"异球为{5-i},其重量为{y-3*z//2},其他球重量为{z//2}")elif x/3 == x//3 and (z/2 < y/4 < x/3 or z/2 > y/4 > x/3): # 异球为jprint(f"异球为{j},其重量为{z-x//3},其他球重量为{x//3}")else: # 异球为iprint(f"异球为{i},其重量为{2*z-x},其他球重量为{x-z}")import randomfor i in range(16):a = [3] * 6 # 初始化每个小球重量均为3num = random.randint(0, 5) # 选择任意一个小球为异球a[num] = a[num] + random.choice([-1,1]) #异球重量可轻可重print(a)fun_3(a, 2, 4)fun_3(a, 2, 5)fun_3(a, 3, 4)fun_3(a, 3, 5)print("#" * 20)

终于搞定了,又可以愉快地玩耍上课了。
需要本文源代码和word文档的,可以加入“Python算法之旅”知识星球参与讨论和下载文件,“Python算法之旅”知识星球汇集了数量众多的同好,更多有趣的话题在这里讨论,更多有用的资料在这里分享。
我们专注Python算法,感兴趣就一起来!
相关优秀文章:
